Integrals, Population, and Density Functions
TLDRThe video script discusses the concept of using integrals to calculate total population in a given region based on population density. It begins with a simple example where the population density is constant, allowing for a straightforward geometric calculation. The script then moves on to more complex scenarios where calculus becomes essential. The first involves a triangular region with a constant density function, and the second deals with a non-uniform density function that decreases as the distance from a fixed point increases. The video uses Riemann sums to approximate the total population and then transitions to definite integrals for precise calculations. The examples demonstrate the application of calculus in real-world problems, such as determining the total population of a town with varying population densities.
Takeaways
- 📚 The video discusses the concept of integrals in relation to population density and how to calculate total population using calculus.
- 🏙️ The script introduces a basic scenario where population density is constant, allowing for geometric calculation of total population without calculus.
- 📏 The first example involves a rectangular town with a constant population density, where the total population is calculated both geometrically and using calculus.
- 📈 The second example features a triangular-shaped town with a constant population density, where calculus is used to find the total population, despite the geometric approach being possible.
- 🏗️ The process involves dividing the town into strips (rectangles), calculating the area of each, and multiplying by the density to find the population within each strip.
- 🧮 Riemann sums are used to approximate the total population by summing the populations of the strips, which becomes a definite integral as the number of strips approaches infinity.
- 📉 The third example involves a non-constant population density function, where the density decreases with distance from the left edge of the town.
- 🔢 The video demonstrates how to calculate the area of a rectangle with a varying height, which corresponds to the population within that strip of the town.
- 🚀 The integral is used to find the total population by summing the populations of an infinite number of strips, which is the limit of the Riemann sum as the number of strips approaches infinity.
- 📊 The video concludes with an example where the population density function is ( \frac{3000}{x^2 + 2} \) people per mile squared, and the town's shape is triangular, necessitating calculus for the solution.
- ✅ The final integral calculation in the third example yields an approximate total population of 18,000 people, which is the expected outcome.
- 🔜 The presenter mentions that future videos will cover radial density problems, which are a variation of the concept discussed in the video.
Q & A
What is the basic concept of the video regarding integrals and population density?
-The video discusses the concept of using integrals to find the total population in a given region where the population density is defined by a function of distance from a specific point in the town.
What is the symbol used to represent population density in the video?
-The symbol used to represent population density in the video is 'Rho (ρ)'.
How is the area of a rectangle related to the calculation of total population in the first example?
-In the first example, the total population is calculated by finding the area of the rectangle (which is the product of its length and width) and then multiplying it by the constant population density per square mile.
What is a Riemann sum and how does it relate to the concept of population density?
-A Riemann sum is a method used to approximate the area under a curve (or in this case, the total population) by dividing the region into rectangles and summing their areas. It is related to population density as it helps to approximate the total population by summing up the populations of these small rectangles.
How does the video use calculus to solve the first example where the population density is constant?
-The video uses calculus by setting up a definite integral with the bounds from 0 to 5 (the x-axis limits of the town) and the function being the constant population density multiplied by the width of the rectangle (4 miles). The integral is then evaluated to find the total population.
What is the shape of the town in the second example and how does it affect the calculation of population?
-The town is shaped like a triangle in the second example. This affects the calculation because the height of each rectangle used in the Riemann sum is no longer constant and must be determined based on the line equation representing the triangle's slope.
null
-null
How does the video calculate the population for a triangular-shaped town?
-The video calculates the population by creating rectangles with a base of Delta X and a height that varies according to the slope of the triangle. The area of each rectangle is then found by multiplying the base by the height, and the population within each rectangle is calculated by multiplying this area by the constant density function.
What is the significance of the integral in calculating the total population when the town's shape is not a simple rectangle?
-The integral is significant as it allows for the precise calculation of the total population by summing up an infinite number of infinitely small rectangles that approximate the area under the population density function over the town's irregular shape.
What is the function for population density in the third example provided in the video?
-The function for population density in the third example is Rho of X, which is 3000 over (X squared plus 2), measured in people per mile squared.
How does the video handle the calculation of population when the density function is not constant?
-When the density function is not constant, the video calculates the population within each rectangle by multiplying the area of the rectangle by the density function evaluated at a specific point within that rectangle. Then, it sums up these values over all rectangles to approximate the total population.
What is the final answer for the total population in the third example using calculus?
-The final answer for the total population in the third example, using calculus, is approximately 18,000.945 people.
What is the next topic the video mentions for future discussion?
-The video mentions that radial density problems will be discussed in a future video, which are a different type of density problems but follow the same integral calculus principles.
Outlines
📊 Calculating Total Population with Constant Density Function
The first paragraph introduces the concept of using integrals to calculate total population based on a given population density function. It explains that the variable X represents the distance from a specific side of a town, and the density function is provided. The example given has a constant density of 200 people per square mile. The town's shape is a rectangle, and the area can be found geometrically, but calculus is used to reinforce understanding. The process involves drawing rectangles (Riemann sums), calculating the area of each, and multiplying by the density to find the population for each strip. The total population is found by summing these values and taking the limit as the number of rectangles (n) approaches infinity, which is the integral from 0 to 5 for this example. The expected answer of 4,000 people is confirmed using this method.
📐 Applying Calculus to Non-Constant Density in a Triangular Region
The second paragraph discusses a scenario where the population density function is not constant and the town's shape is triangular. The density function given is Rho(X) = 3000 / (X^2 + 2) people per square mile, which decreases as the distance from the left edge of the town increases. The process involves creating rectangles with bases of varying heights determined by the town's triangular shape. The area of each rectangle is calculated, and the population within it is found by multiplying the area by the density at that point. The total population is approximated by summing these values and taking the limit as the number of rectangles approaches infinity, resulting in a definite integral from 0 to 6. The integral is evaluated to give an approximate population of 18,095 people. This method is contrasted with the geometric approach, which is only possible due to the constant density and the town's shape.
Mindmap
Keywords
💡Integrals
💡Population Density
💡Riemann Sums
💡Rectangles (in integration)
💡Density Function
💡Geometric Calculation
💡Definite Integral
💡X-axis and Bounds
💡Constant Density
💡Triangular Region
💡Calculus
Highlights
The video discusses the concept of integrals in relation to population density and total population calculation.
Population density is represented by a function, often with X as the distance from a specific point in a town.
The region where the density applies is usually described and often accompanied by a visual representation.
Riemann sums are a recommended approach for solving these problems, by slicing up the area into rectangles.
The first example involves a constant population density (200 people per square mile) across a rectangular town.
The area of the rectangle is calculated geometrically, but calculus is also applied to reinforce understanding.
The total population is found by multiplying the area of the rectangle by the constant density function.
For the second example, the town's shape is triangular, and the population density remains constant, allowing for geometric calculation.
The height of the rectangles in the Riemann sum for the triangular town is determined by the equation 8 - (8/7)X.
The integral calculus method is used to find the total population, yielding the expected result of 5600 people.
The third example features a non-constant density function, Rho(X) = 3000 / (X^2 + 2) people per mile squared.
The population density decreases as the distance from the left edge of the town increases.
The integral is calculated over a triangular region with bounds from 0 to 6, using the density function and the area of rectangles.
The final approximate answer for the total population, using the integral method, is 18,000 + 945 people.
The video concludes with a teaser for another video that will cover radial density problems.
The method of Riemann sums is applicable to both constant and non-constant density functions, demonstrating its versatility.
The video emphasizes the importance of understanding both geometric and calculus-based approaches to solving population density problems.
The practical application of integral calculus in determining total population from density functions is demonstrated through various examples.
Transcripts
Browse More Related Video
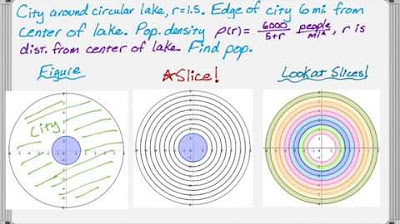
Integrals, Population, and Radial Density Functions

Worked example: problem involving definite integral (algebraic) | AP Calculus AB | Khan Academy

AP Calculus AB 2008 Multiple Choice (Calculator) - Questions 76-92

Analyzing problems involving definite integrals | AP Calculus AB | Khan Academy

2021 AP Calculus AB Free Response #1 Solutions (First Administration)
Math 11 - Section 2.4 (previously section 3.3)
5.0 / 5 (0 votes)
Thanks for rating: