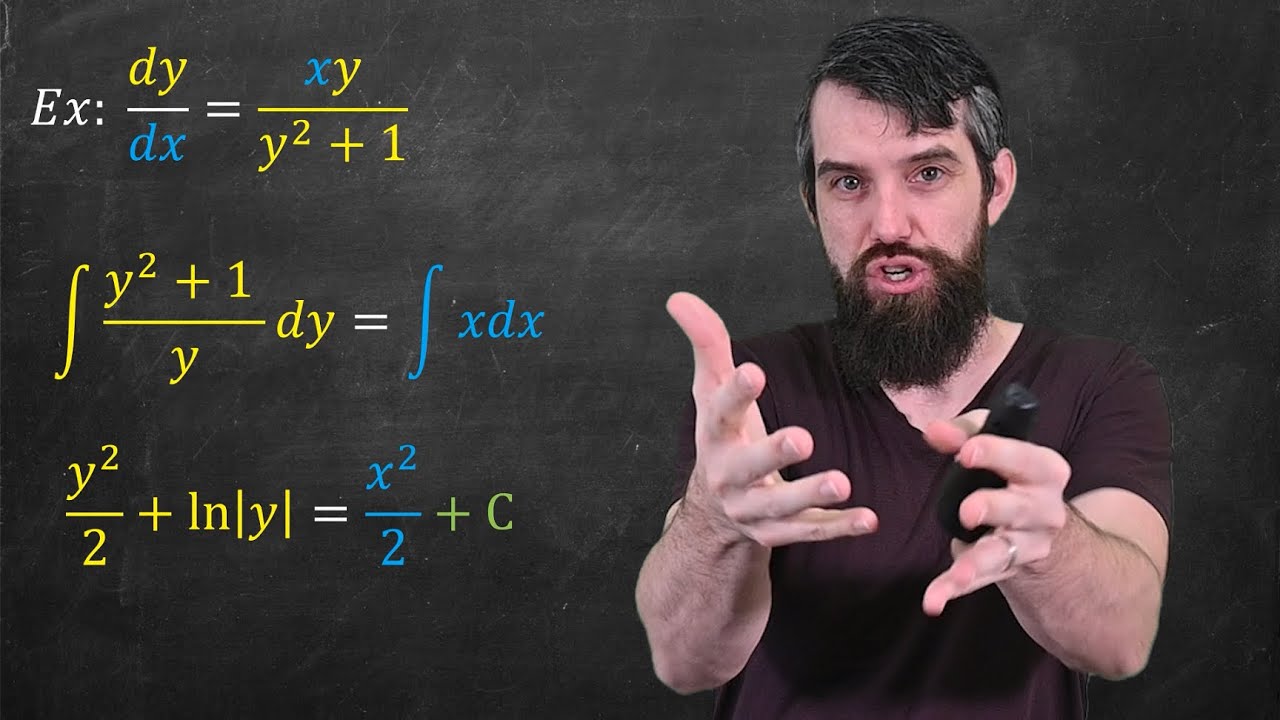Calculus Separation of Variables for Differential Equations
TLDRThe video script presents a comprehensive guide on the concept of separation of variables in solving differential equations, a method that may initially intimidate students. The speaker demystifies the process by emphasizing its simplicity, comparing it to solving two separate integration problems. The script outlines the steps to separate the independent variable on one side and the dependent variable on the other, followed by integration. It also addresses common concerns, such as the absence of the independent variable post-separation and the handling of constant multiples. The video includes detailed examples, starting with a problem involving the rate of change of a quantity 'H' with respect to time 'T', and another involving 'W' with respect to time 'T'. Each example is meticulously solved, highlighting the integration process, the importance of considering the initial conditions, and the need to account for the domain of the solution. The summary aims to reassure viewers that with a clear understanding of the principles, solving separable differential equations is quite manageable.
Takeaways
- 📚 Separation of variables is a method that can be intimidating but shouldn't be, as it involves solving two separate integration problems.
- 🔍 The process involves separating the independent variable on one side and the dependent variable on the other.
- ⚖️ When separating variables, terms involving the independent variable are moved to the right, and terms involving the dependent variable are moved to the left.
- 🧮 A constant multiple, if present, is often left on or moved to the right-hand side of the equation for ease of integration.
- 🚫 There's no requirement for the independent variable to be explicitly present before integration; it's a common misconception that can cause unnecessary anxiety.
- 🌟 Integration is performed after separating variables, with the constant of integration (C) typically placed on the side with the independent variable.
- 📉 For differential equations like dh/dt = -1/4(H - 27), separation leads to an integral involving the natural logarithm function, and the absolute value is crucial.
- ✅ Use initial conditions to solve for constants in the equation, substituting known values to find the constant multiplier.
- 🔗 Exponentiation is a common step after integrating to isolate the dependent variable, which helps in solving for the variable of interest.
- 📈 The solution to a differential equation must be continuous on an interval containing the initial condition, which can affect the domain of the solution.
- 🛑 Be aware of discontinuities in the differential equation, such as vertical asymptotes, as they can limit the domain of the solution.
- 📝 When providing the final answer, include the domain of the solution to fully solve the separable differential equation.
Q & A
What is the general approach to solving problems using the separation of variables method?
-The general approach involves separating the independent variable on one side and the dependent variable on the other, and then integrating both sides to solve the problem.
What are some common notations used in separation of variables that represent derivatives?
-Common notations include dy/dx, dV/dR, and dh/dt, where the variable in the denominator represents the independent variable.
What should you do with the constant multiple when separating variables?
-It is recommended to leave the constant multiple on the right-hand side of the equation to simplify the integration process.
Can the independent variable always be assumed to be present before integration?
-No, there is no guarantee that the independent variable will be present before integration. It's important not to be alarmed if it is missing.
How should you handle the constant of integration, C, when integrating?
-You should place the constant C on the side with the independent variable after integrating both sides of the equation.
In the provided example, what is the differential equation for H?
-The differential equation for H is dh/dt = -1/4(H - 27), with the initial condition H(0) = 91.
What is the significance of the absolute value in the integral of the left-hand side of the differential equation for H?
-The absolute value ensures that the result of the integration is defined even when dealing with quantities that could be negative.
How do you find the value of C in the second example with the differential equation DW/DT = W^2/t - 4?
-You use the initial condition W(3) = 2 to solve for C by substituting the values into the separated equation and isolating C.
Why is it important to consider the domain of the solution when solving a differential equation?
-The solution must be continuous on an interval containing the initial condition. Considering the domain ensures that the solution is valid and applicable across the specified range of the independent variable.
What is the final form of the solution for the second example with the differential equation DW/DT = W^2/t - 4?
-The solution is W = 1/(1/2 - ln|t - 4|) with the domain T < 4, as the initial condition W(3) = 2 falls within this domain.
What is the key takeaway from the video regarding solving separable differential equations?
-The key takeaway is to separate the variables, integrate both sides, handle constants appropriately, and be mindful of the domain of the solution to ensure the solution is valid and continuous.
Outlines
📚 Introduction to Separation of Variables
This paragraph introduces the concept of separation of variables, a technique that can seem intimidating but is essentially about solving two separate integration problems. The speaker emphasizes the importance of identifying the independent variable (usually found in the denominator) and the dependent variable (in the numerator), and then rearranging the equation to isolate these variables on opposite sides. The process involves moving terms involving the independent variable to one side of the equation and those involving the dependent variable to the other. The speaker also advises on handling constant multiples and reassures that the independent variable may not always be explicitly present before integration, which should not cause alarm. An example problem involving the differential equation dh/dt = -1/4(H - 27) with the initial condition H(0) = 91 is presented, and the separation process is demonstrated, including the integration steps and the application of the initial condition to find the particular solution.
🔍 Solving a Separable Differential Equation with Initial Condition
The second paragraph delves into solving a specific separable differential equation, DW/DT = W^2 / (T - 4), given the initial condition W(3) = 2. The speaker points out the discontinuity at T = 4 due to the t - 4 term in the denominator, noting that the solution must be continuous on an interval containing the initial condition. The choice is made to consider the domain where T < 4 to accommodate the initial condition at T = 3. The equation is separated into two integrals, one for W and the other for T, and the integration is performed. The initial condition is then used to solve for the constant C, leading to the particular solution for W in terms of T. The speaker emphasizes the importance of including the domain with the solution and presents the final answer, ensuring that the domain T < 4 is clearly stated.
Mindmap
Keywords
💡Separation of Variables
💡Differential Equation
💡Integration
💡Independent Variable
💡Dependent Variable
💡Constant Multiple
💡Natural Logarithm
💡Absolute Value
💡Initial Condition
💡Domain
💡Exponentiation
Highlights
Separation of variables is a technique that can be intimidating but shouldn't be.
The process involves separating the independent and dependent variables and then integrating.
When separating variables, terms involving the independent variable should be on the right.
Dependent variables like Y, V, and H should be moved to the left side of the equation.
A constant multiple in the equation is often left or moved to the right-hand side for easier integration.
There's no requirement for the independent variable to be present before integration.
An example given is DP/DT = 6P, where the independent variable T is not explicitly shown.
Integration is performed on both sides of the equation as separate problems.
When integrating, the constant of integration (C) is placed on the side with the independent variable.
An example problem involves solving dh/dt = -1/4(H - 27) with H(0) = 91, derived from the 2017 AP exam.
Separating variables in the example results in an equation involving the natural logarithm of (H - 27).
The absolute value is important in integration to avoid complex numbers.
The solution involves exponentiating to solve for H, resulting in H - 27 = C * e^(-1/4T).
Using the initial condition H(0) = 91 allows solving for the constant C.
The final answer for the example is H = 27 + 64e^(-1/4T).
Another example problem involves solving dW/dt = W^2/t - 4 with W(3) = 2, noting the discontinuity at t=4.
The solution's domain is determined by the initial condition, in this case, t < 4.
The solution to the differential equation must be continuous on an interval containing the initial condition.
The final solution for W includes the domain restriction and is given as 1/W = -1/2 - ln|t - 4| for t < 4.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: