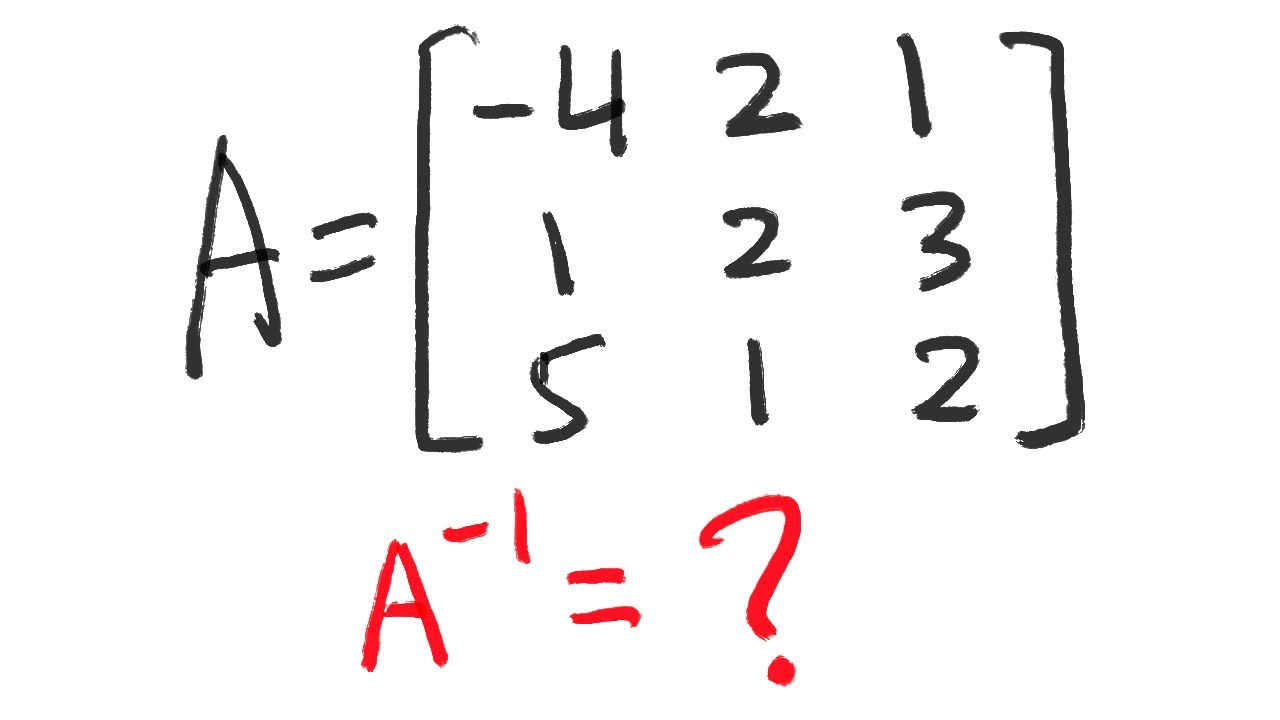How to Invert Matrices - Exercises (Step by Step)
TLDRThis video tutorial offers a step-by-step guide on calculating the inverse of 2x2 and 3x3 matrices, a common challenge in mathematics and physics. The presenter begins by explaining how to compute the determinant, crucial for finding the inverse. For 2x2 matrices, the process involves transposing and scaling a modified version of the original matrix. The video then tackles 3x3 matrices, emphasizing systematic calculation and the use of cofactor expansion for determining elements of the inverse. The presenter also provides a quick check method using matrix multiplication to confirm the accuracy of the calculated inverse. The video concludes with a reminder that matrices with a determinant of zero or with rows/columns that are multiples of each other do not possess an inverse, saving unnecessary calculations.
Takeaways
- 📚 The video is an educational session focused on teaching the calculation of the inverse of 2x2 and 3x3 matrices.
- 🔍 The first step in calculating the inverse of a matrix is to find its determinant.
- 🤔 A common mistake is made when calculating the inverse matrix, so the video emphasizes a systematic, step-by-step approach.
- 🔄 To find the inverse matrix, one must transpose the matrix and then multiply each element by the reciprocal of the determinant.
- 💡 The video provides a trick to verify the correctness of the calculated inverse matrix: multiply it with the original matrix to obtain an identity matrix.
- 🌟 The video highlights the importance of checking one's work to ensure accuracy and understanding of the process.
- ❌ The inverse of a matrix does not exist if the determinant is zero, as is the case when one row or column is a multiple of another.
- 🚀 The video demonstrates how to quickly calculate the inverse of a diagonal matrix by inverting each diagonal element individually.
- 📈 The video includes examples and exercises to practice the concepts taught, with timestamps provided in the comments for easy navigation.
- 🎓 The video aims to help students who struggle with the concept of matrix inversion to gain a better understanding and confidence.
- 📌 The video concludes with a reminder that breaking down complex tasks into smaller steps can minimize errors and improve understanding.
Q & A
What is the main focus of the video?
-The main focus of the video is to teach viewers how to calculate the inverse of 2x2 and 3x3 matrices in a step-by-step manner to reduce the chances of making mistakes.
How is the determinant of a 2x2 matrix calculated?
-The determinant of a 2x2 matrix is calculated by multiplying the elements in the top row and subtracting the product of the elements in the bottom row. For example, for a matrix (a b; c d), the determinant is ad - bc.
What is the first step in calculating the inverse of a matrix?
-The first step in calculating the inverse of a matrix is to find the determinant of the matrix.
How can you check if you have calculated the correct inverse matrix?
-You can check if you have calculated the correct inverse matrix by multiplying the original matrix with the calculated inverse matrix. If the result is an identity matrix, then the inverse matrix is correct.
What is a quick way to determine if a 2x2 matrix has an inverse?
-A quick way to determine if a 2x2 matrix has an inverse is to check if one row or column is a multiple of another. If so, the determinant will be zero, and the matrix does not have an inverse.
How is the inverse of a 3x3 matrix calculated?
-The inverse of a 3x3 matrix is calculated by taking the reciprocal of the determinant, and then multiplying it by the transpose of the matrix obtained by replacing each element with its corresponding cofactor.
What is a cofactor in the context of matrix inversion?
-A cofactor in the context of matrix inversion is the determinant of the 2x2 matrix obtained by removing the row and column of the current element, with a plus or minus sign depending on the position of the element (even row and even column position means a plus sign, otherwise a minus sign).
What is the identity matrix for 2x2 and 3x3 matrices?
-The identity matrix for 2x2 matrices is (1 0; 0 1), and for 3x3 matrices, it is (1 0 0; 0 1 0; 0 0 1).
How can you quickly calculate the inverse matrix of a 3x3 matrix with elements only on the diagonal?
-For a 3x3 matrix with elements only on the diagonal, you can quickly calculate the inverse by inverting each diagonal element separately. For example, if the matrix is (a b 0; 0 c d; 0 0 e), the inverse will be (1/a 0 0; 0 1/c 0; 0 0 1/e).
What is the determinant of a 3x3 matrix with only diagonal elements?
-The determinant of a 3x3 matrix with only diagonal elements is the product of the diagonal elements. For example, for a matrix (a b 0; 0 c d; 0 0 e), the determinant is a*c*e.
How can you tell if a matrix does not have an inverse?
-A matrix does not have an inverse if its determinant is zero. Additionally, if there is a row or column that is a multiple of another, the matrix is singular and does not have an inverse.
Outlines
📚 Introduction to Matrix Inversion
This paragraph introduces the topic of matrix inversion, specifically focusing on 2x2 and 3x3 matrices. The speaker explains that many students struggle with this concept and aims to provide a systematic, step-by-step approach to reduce mistakes. The video also promises a trick to verify the correctness of the calculated inverse matrix. The first exercise involves calculating the inverse of a 2x2 matrix, starting with determining the determinant and proceeding with the transposition of the matrix elements to find the inverse.
🧠 Verifying the Inverse Matrix
In this paragraph, the speaker demonstrates how to verify the calculated inverse matrix by multiplying it with the original matrix and checking if the result is the identity matrix. The process is illustrated using a 2x2 matrix example. The speaker emphasizes the importance of this verification step to ensure accuracy and correct any potential errors in the calculation of the inverse matrix.
🔢 Calculating the Inverse of a 3x3 Matrix
The speaker moves on to the next exercise, which involves calculating the inverse of a 3x3 matrix. The process is similar to the 2x2 matrix, starting with calculating the determinant and then using it to find the inverse matrix. The paragraph details the steps of ignoring certain rows and columns to find the elements of the transposed matrix, which are then used to calculate the inverse. The speaker also provides a quick method for checking the correctness of the inverse by multiplying it with the original matrix.
🚫 Matrix Inversion Limitations
This paragraph discusses the limitations of matrix inversion, specifically when the determinant is zero. The speaker explains that a matrix with a zero determinant does not have an inverse, as there is no matrix that can be multiplied with it to yield the identity matrix. The example given involves a 2x2 matrix with rows that are multiples of each other, leading to a determinant of zero and confirming that an inverse matrix does not exist for this case.
📈 Inverse of a Diagonal Matrix
The speaker explains the process of calculating the inverse of a matrix with elements only on the diagonal. This is a special case where the inverse can be found simply by inverting each diagonal element individually. The process is illustrated with a 3x3 matrix example, and the speaker shows that the resulting inverse matrix has each element inverted from the original matrix.
🤔 Identifying Non-invertible Matrices
In the final exercise, the speaker guides the viewer on how to identify a non-invertible matrix by observing the relationship between its rows. The example matrix has rows that are multiples of each other, indicating that the determinant will be zero and the matrix does not have an inverse. This observation helps to save time by avoiding unnecessary calculations when dealing with non-invertible matrices.
👋 Conclusion and Encouragement
The speaker concludes the session by encouraging viewers to practice the techniques learned for calculating the inverse of matrices. They emphasize that while it can be a tedious process, breaking it down into smaller steps can minimize mistakes. The speaker also invites viewers to like the video, subscribe for updates, and looks forward to the next video session.
Mindmap
Keywords
💡Inverse Matrix
💡Determinant
💡Matrix Transposition
💡Matrix Multiplication
💡Identity Matrix
💡Cofactor
💡Adjugate Matrix
💡Zero Matrix
💡Diagonal Elements
💡Row Multiplication
Highlights
The video focuses on calculating the inverse of 2x2 and 3x3 matrices, a topic that many students struggle with.
The presenter uses a systematic step-by-step approach to reduce the chances of making mistakes while calculating the inverse matrices.
A trick is shared to verify the correctness of the calculated inverse matrix by multiplying it with the original matrix to obtain an identity matrix.
The video provides a detailed explanation of how to calculate the determinant of a 2x2 matrix, which is the first step in finding the inverse.
The process of transposing a 2x2 matrix is explained, which involves swapping rows and columns to find the elements of the inverse matrix.
The video demonstrates how to calculate the inverse of a 3x3 matrix, emphasizing the importance of calculating the determinant and transposing the matrix correctly.
A method for quickly determining when a matrix does not have an inverse is presented, saving time by identifying rows or columns that are multiples of each other.
The video explains the pattern of alternating signs in the inverse matrix of a 2x2 matrix and why this pattern exists.
A specific example of a 2x2 matrix is used to illustrate the entire process of finding its inverse, from calculating the determinant to verifying the result.
The video touches on the concept of the identity matrix and its role in verifying the inverse of a matrix.
The process of calculating the determinant of a 3x3 matrix is outlined, which is more complex but follows the same principles as for a 2x2 matrix.
The video provides a clear and concise explanation of how to find the inverse of a matrix with elements only on the diagonal, simplifying the process.
The importance of checking the determinant to quickly determine if a matrix has an inverse is emphasized, highlighting the efficiency this provides.
The video concludes with a review of the key points and encourages practice to become more familiar with the process of calculating inverse matrices.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: