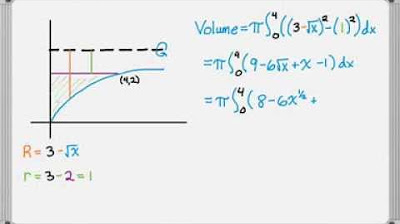Volume of Revolution Examples - Vertical Axis
TLDRThe video script discusses the concept of calculating volume by revolving a region around a vertical axis, which can be challenging but follows a similar approach to horizontal axis rotation. The presenter demonstrates two examples: the first involves revolving the region bounded by y = √2x and x = 0 around the y-axis, using the equation x = y^2 to find the radius and set up the volume integral. The second example revolves around the x-axis at x = 4, with the outer and inner radii determined by the given axis and the curve y = x^2. The process involves setting up the volume integral, simplifying, and finding the anti-derivative before evaluating the integral. The key difference in the vertical axis rotation is solving for x instead of y, but the overall method remains consistent. The video aims to help viewers understand the process and apply it to similar problems.
Takeaways
- 📚 The video discusses the concept of finding the volume of a solid formed by rotating a region around a vertical axis, which some find challenging but is fundamentally similar to rotating around a horizontal axis.
- 🔍 The key difference when rotating around a vertical axis is that equations are solved for 'x' instead of 'y'.
- 📈 A graph is created to visualize the region bounded by the given function and the axis of rotation.
- ✍️ The curve y = √(2x) is relabeled as x = y^2 to facilitate the setup for volume calculation when rotating around the y-axis.
- 📐 The radius for the volume calculation is determined by the distance from the axis to the outer curve, which in this case is y^2.
- 🧮 The volume is calculated using the method of integration, where the area of the shape formed by the radius and the rotation is integrated.
- 🔁 For the second example, the region is rotated around the x = 4 line, and the process is similar to the first, but with adjustments made for the new axis of rotation.
- 📐 In the second example, the big radius is calculated as 4 - 0, as the region extends from x = 4 to the y-axis.
- 📐 The small radius in the second example is calculated as 4 - y^2, representing the distance from the axis to the inner edge of the region.
- ✅ The volume calculation involves squaring the difference between the big and small radii and integrating the result.
- 🔢 The final step is to evaluate the integral, which in the second example results in a volume of (224π)/15.
- 🎓 The video emphasizes that the process for calculating volume around a vertical axis is essentially the same as for a horizontal axis, with the main change being the variable used in the equations.
Q & A
What is the topic of the video?
-The video is about calculating the volume of solids formed by rotating a region around a vertical axis.
Why might rotating around a vertical axis be considered more challenging?
-Rotating around a vertical axis can be more challenging because it requires solving equations for 'x' instead of 'y', which is a different approach than what is typically used.
What is the first step the presenter takes in solving the volume problem?
-The first step is to create a graph of the region bounded by the given equation y = √(2x) and x = 0.
How does the presenter label the curve in the graph?
-Instead of labeling the curve as y = √(2x), the presenter labels it as x = y^2 to simplify the process of rotating around the y-axis.
What is the 'big radius' in the context of the volume calculation?
-The 'big radius' refers to the horizontal distance from the y-axis to the outer curve of the region being rotated.
What is the formula for the volume of a solid of revolution around a vertical axis?
-The formula for the volume is π * ∫[R(x)^2 - r(x)^2] dx, where R(x) is the big radius and r(x) is the small radius.
What is the difference in the approach when rotating around the x=4 line?
-When rotating around x=4, the axis is horizontal, and the big radius is found by going from x=4 to the y-axis (x=0), and the small radius is found by going from the axis to the inner edge of the region.
How does the presenter find the volume when rotating around x=4?
-The presenter calculates the volume by integrating the squared difference between the big radius (4 - 0) and the small radius (4 - y^2) with respect to x.
What is the final result for the volume when rotating around the x=4 line?
-The final result for the volume is 224π/15 cubic units.
Why does the presenter mention that the sign of the radius values doesn't matter when squaring them?
-The sign doesn't matter because when you square a number, whether it's positive or negative, the result is always positive.
What is the key takeaway from the video for someone familiar with volume calculations around a horizontal axis?
-The key takeaway is that the process for calculating volume around a vertical axis is similar to that around a horizontal axis, with the main difference being the variable (x instead of y) for which you solve the equations.
Outlines
📚 Introduction to Volume by Revolution Around a Vertical Axis
The video begins with an introduction to calculating the volume of a solid formed by rotating a region around a vertical axis, which some find challenging. The presenter emphasizes that the process is similar to calculating volume around a horizontal axis, but one must solve equations for 'X' instead of 'Y'. The problem involves rotating the region bounded by the curve Y = √(2X) and the X-axis around the Y-axis.
Mindmap
Keywords
💡Volume
💡Washers
💡Solid of Revolution
💡Vertical Axis
💡Equations
💡Integration
💡Anti-Derivative
💡Graph
💡Radius
💡Y-axis
💡Calculus
Highlights
The video discusses the concept of volume by disks and washers around a vertical axis, which can be challenging for some.
It emphasizes that solving equations for X instead of Y is key when dealing with a vertical axis rotation.
A graph is created to visualize the region bounded by y = √(2x) and x = 0.
The curve y = √(2x) is relabeled as x = y^2 for clarity when rotating around the Y-axis.
The big radius for the volume calculation is determined by the horizontal distance from the Y-axis to the outer curve (y^2).
The volume equation is set up by considering the difference between the outer and inner radii squared.
The process is simplified by finding an anti-derivative and then evaluating it.
A second example is presented, revolving around the x-axis at x = 4.
For the second example, the big radius is calculated as 4 - y^2, representing the distance from the axis to the outer edge.
The small radius is determined by the distance from the axis to the inner edge of the region.
The volume calculation involves squaring the difference between the outer and inner radii.
Algebraic manipulation is used to expand and collect like terms for the volume equation.
The final step involves plugging in values to find the volume, with attention given to obtaining positive values for the radii.
The video concludes with a worked example that results in a volume of 224π/15.
The main difference in calculating volume around a vertical axis is solving equations for X.
The video aims to help viewers understand the process and provides encouragement for tackling such problems.
The presenter assures that if one is proficient in calculating volumes around a horizontal axis, the process for a vertical axis is quite similar.
The importance of correctly labeling curves and axes is highlighted for clarity in the volume calculation process.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: