AP PHYSICS 1: Unit 6 FRQs 1 and 2 (AP Classroom)

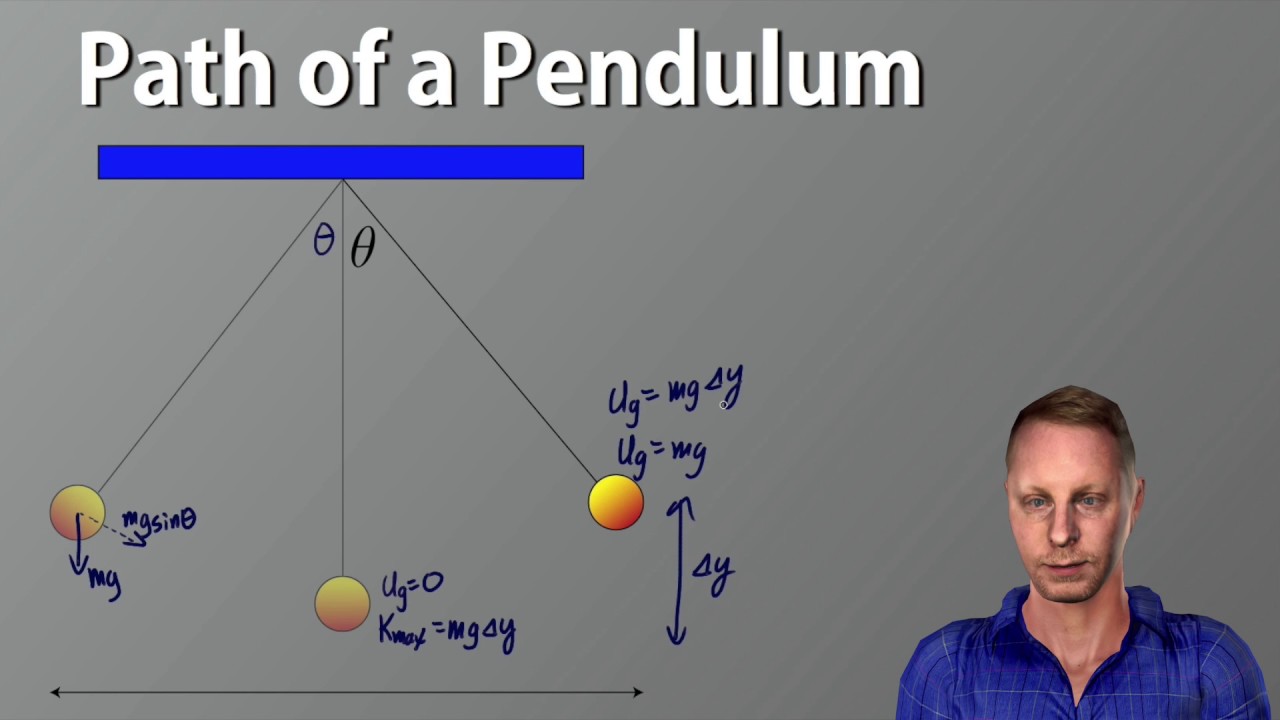
This paragraph introduces the topic of Simple Harmonic Motion from AP Physics 1. Mr. Heinrich discusses an experiment where students are given equipment to determine the acceleration due to gravity by putting a sphere into simple harmonic motion. The focus is on understanding the basic physics principle behind the pendulum motion and the equation that describes it. The equation mentioned is T = 2π√(l/g), which relates the period of the pendulum to its length and the gravitational acceleration. The paragraph emphasizes the importance of this concept for the AP test and provides context for the experiment.

In this paragraph, the speaker outlines the experimental setup and procedure to determine gravitational acceleration using a pendulum. The students are required to measure quantities such as time, length, and angle of release using appropriate equipment like a stopwatch, meter stick, and protractor. The speaker explains the importance of releasing the pendulum from an angle less than 15 degrees for it to be considered simple harmonic motion. The procedure involves timing multiple cycles of the pendulum's motion and averaging these measurements to reduce error. The goal is to develop a method to accurately measure and use these values in the experiment.

This paragraph discusses the data analysis and graphing process for the experiment. The speaker explains how to use the collected data to graph the relationship between different quantities, such as the period (T) and the length of the pendulum string (L), in order to determine the acceleration due to gravity (g). The speaker provides a detailed explanation of how to manipulate the equation of motion to solve for g and how to represent this relationship graphically. The focus is on understanding the slope of the best-fit line and how it can be used to calculate the gravitational acceleration near Earth's surface.

In this paragraph, the speaker addresses a hypothetical scenario where the string of the pendulum is cut. The task is to predict the motion of the sphere in terms of its displacement, initial speed, and acceleration after the string is severed. The speaker explains that the sphere would be at rest at the point of cutting, with zero initial speed and would then begin to freefall with an acceleration equal to g (9.8 m/s^2). The displacement of the sphere would be negative, indicating that it would move away from the equilibrium position in the direction of the cut string.

This paragraph shifts focus to another type of simple harmonic oscillator - a spring-mass system. The speaker describes a scenario where a block attached to a horizontal spring is stretched and then released, undergoing simple harmonic motion. The speaker is tasked with creating a graph of force versus horizontal position based on the potential energy graph provided. The explanation includes understanding the relationship between potential energy, force, and displacement, and how these quantities change as the block moves from one position to another. The speaker emphasizes the linear relationship between force and displacement in the absence of friction and other external forces.

The final paragraph discusses the kinetic energy of the spring-mass system and the calculation of the spring constant (k). The speaker is provided with a graph of potential energy versus displacement and is asked to calculate the period of the system and the spring constant using the given potential energy value at a specific displacement. The speaker uses the relationship between work, energy, and force to explain the linearity of the force-displacement graph and provides the method to calculate the spring constant. The spring constant is found to be 320 N/m, which is verified against the given potential energy value.