2021 Live Review 6 | AP Physics 1 | Understanding Simple Harmonic Motion
TLDRIn this engaging lesson, Joshua Beck delves into the concept of simple harmonic motion, addressing students' feedback for more experimental design assistance. Beck introduces the fundamentals of simple harmonic motion, discussing amplitude, frequency, and period. He then explores the requirements for an object to oscillate in this manner, highlighting the role of net force and the characteristics of springs. The lesson progresses to discuss the relationship between force, acceleration, and velocity with displacement and time. Beck also presents a practical experiment to determine an unknown spring constant, emphasizing the importance of understanding the relationship between variables and the experimental procedure. The session concludes with Beck addressing the effects of changing mass and spring constant on the period of oscillation, providing valuable insights for students preparing for the AP Physics 1 exam.
Takeaways
- 📚 The session focuses on simple harmonic motion and incorporates experimental design based on student feedback.
- 👂 The instructor, Joshua Beck, emphasizes that student voices are heard and their requests for additional help are acknowledged.
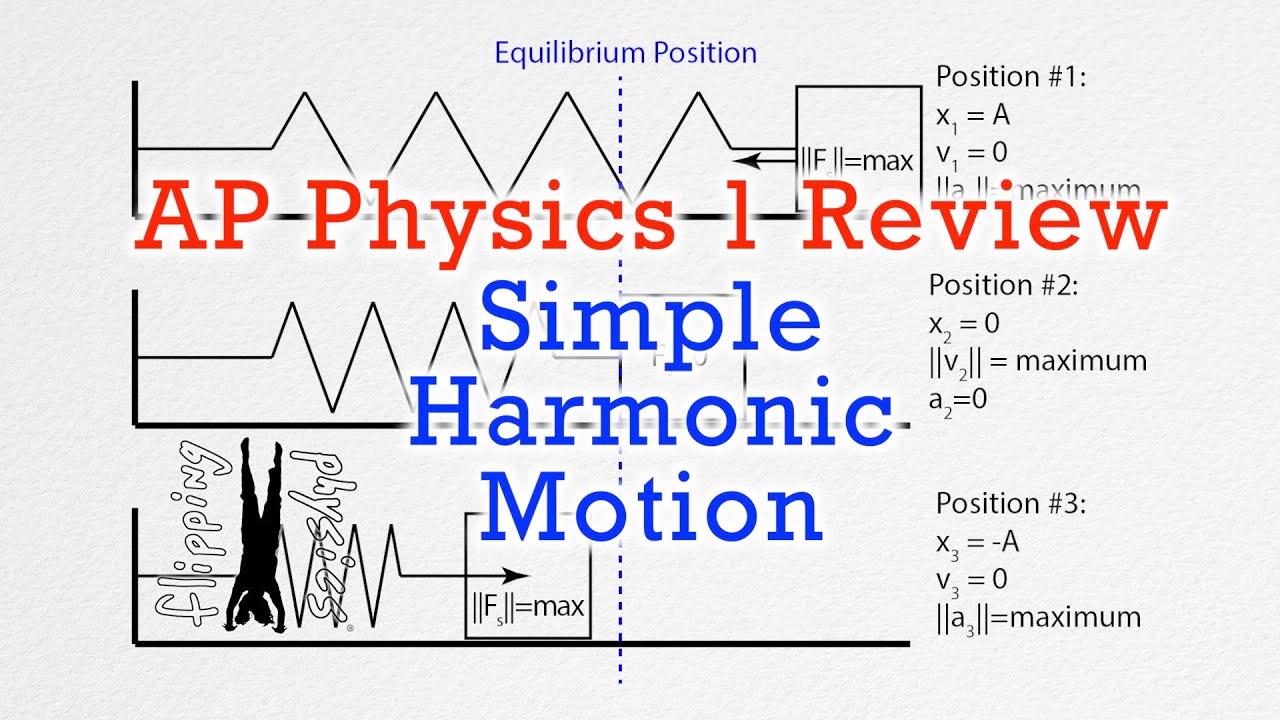
- 📈 Simple harmonic motion is characterized by an object oscillating between two positions with a maximum displacement (amplitude) and a periodic frequency.
- 📊 The position of a simple harmonic oscillator is described by a cosine curve, with the faster the oscillation, the more compressed the pattern.
- 🔧 For an object to oscillate in simple harmonic motion, a net force opposite to the displacement is required, which should be proportional to the displacement.
- 🏋️♂️ Springs are ideal for simple harmonic motion due to their ability to exert a force proportional to the displacement when stretched or compressed.
- 📐 The equilibrium position of a mass-spring system is crucial for simplifying calculations, as it allows measuring displacement relative to a balanced point.
- 📉 The maximum force in a mass-spring system occurs at the amplitude points, and it can be calculated using the spring constant (k) and the displacement (x).
- 🚫 It's important to note that the force in simple harmonic motion varies with displacement, affecting acceleration and velocity at different points in the cycle.
- 🔄 The period of oscillation is independent of the amplitude and is affected by the mass and spring constant, with larger masses resulting in longer periods and stronger springs resulting in shorter periods.
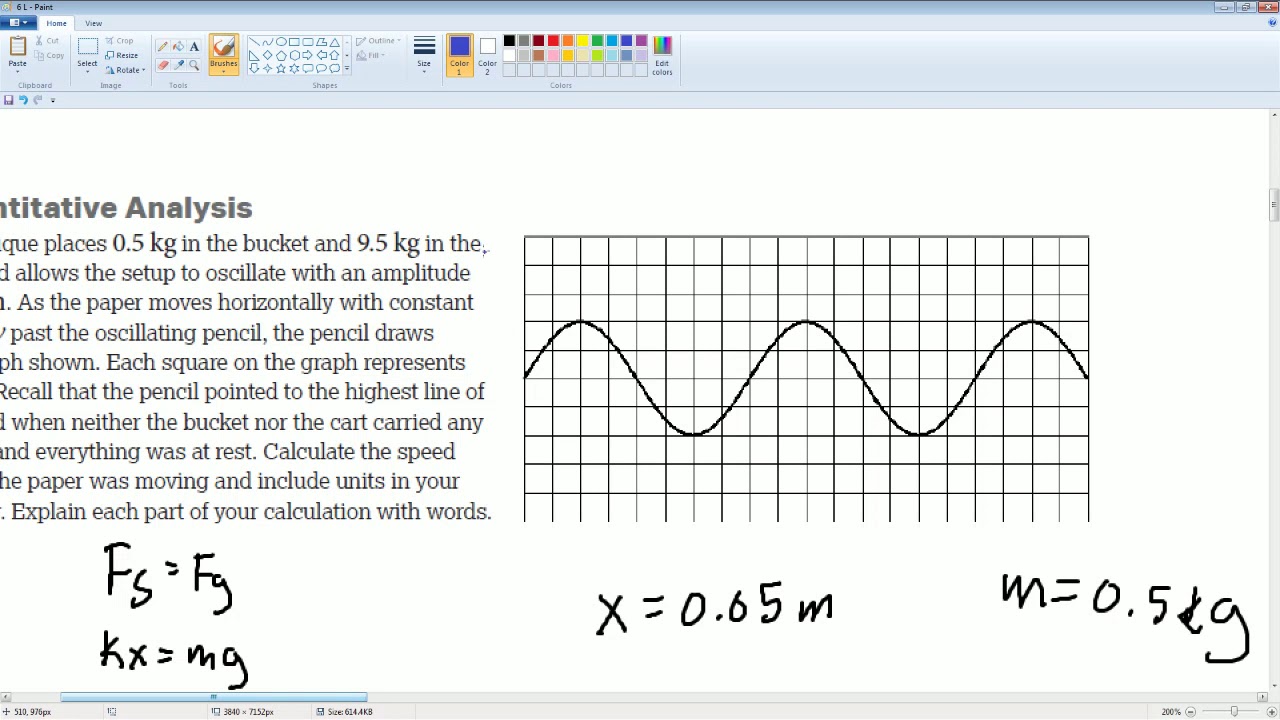
- 🔧 An experiment to determine the spring constant involves varying the mass while keeping the spring constant and measuring the period, which can then be used to calculate k.
Q & A
What is simple harmonic motion and how can you identify it?
-Simple harmonic motion is a type of periodic motion where an object oscillates between two positions with a regular pattern. You can identify it by observing an object moving back and forth through a fixed point, called the equilibrium position, with a constant amplitude, and a periodic frequency or period.
What are the key characteristics of simple harmonic motion in terms of amplitude and frequency?
-In simple harmonic motion, the amplitude represents the maximum displacement of the object from its equilibrium position, and it does not affect the frequency. The frequency is the number of complete oscillations per second, and inversely, the period is the number of seconds for one full oscillation. The frequency and period are inversely related, but they are independent of the amplitude.
What force requirements must be met for an object to oscillate in simple harmonic motion?
-For an object to oscillate in simple harmonic motion, there must be a net force acting in the opposite direction of the displacement. This net force must be proportional to the displacement and capable of changing directions as the object moves. An example of such a force is the restoring force of a spring.
How does the orientation of a mass-spring system affect its simple harmonic motion?
-The orientation of a mass-spring system does not fundamentally affect its simple harmonic motion as long as the displacement is measured from the equilibrium position. Whether the spring is vertical, horizontal, or on an incline, the mathematical treatment remains the same when displacement is referenced to the equilibrium position.
What is the relationship between the force and displacement in a mass-spring system?
-In a mass-spring system, the net force acting on the mass is proportional to the displacement from the equilibrium position and is directed towards that equilibrium position. This relationship is described by Hooke's Law, where the force (F) is equal to the spring constant (k) times the displacement (x), or F = kx.
How can you calculate the maximum force in a mass-spring system?
-The maximum force in a mass-spring system can be calculated by multiplying the spring constant (k) by the amplitude (a), which is the maximum displacement from the equilibrium position. This gives you the net force experienced by the mass at the extreme points of its oscillation.
What happens to the period of oscillation if the mass attached to the spring is increased?
-If the mass (m) attached to the spring is increased, the period (T) of oscillation will increase. This is because the period is inversely proportional to the square root of the mass, as described by the formula T = 2π√(m/k).
How does the spring constant (k) affect the period of oscillation?
-An increase in the spring constant (k) will result in a decrease in the period (T) of oscillation. This is because the period is inversely proportional to the square root of the spring constant, as shown in the formula T = 2π√(m/k).
What are the maximum and minimum values of acceleration and velocity in simple harmonic motion?
-In simple harmonic motion, the maximum acceleration occurs at the equilibrium position, where the velocity is zero, and the minimum acceleration occurs at the amplitude positions, where the velocity is at its maximum. Conversely, the maximum velocity occurs at the equilibrium position, and the minimum velocity (which is zero) occurs at the amplitude positions.
How can you determine the spring constant (k) experimentally using the period of oscillation?
-You can determine the spring constant (k) experimentally by measuring the period of oscillation (T) for a mass-spring system and using the formula T = 2π√(m/k). By rearranging the formula to solve for k, you can calculate the spring constant as k = (4π²m)/T².
What is the significance of the slope in a force versus position graph for a spring?
-The slope in a force versus position graph for a spring represents the spring constant (k). The steeper the slope, the higher the spring constant, indicating a stiffer spring that requires more force to cause the same displacement.
Outlines
📚 Introduction to Simple Harmonic Motion and Feedback
The speaker, Joshua Beck, begins by addressing the audience and acknowledging the feedback received through a form. He appreciates the audience's engagement and assures them that their voices are heard. He then introduces the topic of the day, which is simple harmonic motion, and mentions that he will also cover experimental design based on the audience's request. Beck provides an overview of what simple harmonic motion is, describing it as an oscillation between two positions with a maximum displacement known as amplitude. He explains the concepts of frequency and period, using a visual aid to illustrate the motion and how it can be represented graphically. Beck emphasizes the importance of understanding the underlying forces and requirements for an object to oscillate in simple harmonic motion, using a spring as an example to demonstrate how the force changes in response to displacement.
📐 Analysis of Simple Harmonic Motion: Force, Acceleration, and Energy
Continuing the discussion on simple harmonic motion, Beck delves into the specifics of force and acceleration within this context. He clarifies that the force experienced by an object in simple harmonic motion is proportional to its displacement and changes direction as the object moves. Beck uses an experiment with two springs and a mass to illustrate that the frequency of oscillation remains constant despite different masses and spring constants. He further explains the relationship between force and position, and how it can be visualized graphically. Beck also touches on the concepts of maximum acceleration and velocity, and where these occur in the oscillation cycle. He emphasizes the importance of understanding that force is not constant and varies as the object moves through its cycle.
📊 Graphs and Predictions in Simple Harmonic Motion
In this section, Beck focuses on the graphical representation of simple harmonic motion, specifically discussing the relationship between force, position, velocity, and acceleration. He uses a video and force sensor data to demonstrate how these quantities change over time and position. Beck highlights the maximum and minimum values of force, velocity, and acceleration and explains when these occur during the oscillation. He also discusses the concept of energy in the context of simple harmonic motion, differentiating between kinetic and potential energy. Beck encourages the audience to make predictions about how changes in mass and spring constant affect the period of oscillation, and then confirms these predictions with experimental data.
🧪 Designing an Experiment to Determine the Spring Constant
Beck shifts the focus to experimental design, aiming to determine the spring constant (k) of an ideal spring. He outlines three possible approaches: force analysis, energy analysis, and oscillation analysis. Beck decides to concentrate on the oscillation aspect, using the period of oscillation as a means to find k. He explains the mathematical relationship between the period, mass, and spring constant, and how this can be rearranged to solve for k. Beck then describes a step-by-step procedure for conducting the experiment, including the selection of equipment, collection of data, and the process of graphing and analyzing the results to find the spring constant. He emphasizes the importance of collecting multiple data points and the process of linearizing the data to find a straight line, which allows for an accurate calculation of k.
🔄 Effects of Changing Mass and Spring Constant on the Period
Beck explores the effects of changing the mass and spring constant on the period of oscillation in a mass-spring system. He uses the previously established formula for the period and applies the concept of the factor of change to demonstrate how doubling the spring constant would affect the period. Beck then explains how to maintain the same period if the spring constant is changed, by adjusting the mass accordingly. He further discusses what would happen if both the mass and spring constant are altered simultaneously, using the same factor of change approach. Beck's explanation helps to clarify how these variables interact and influence the period of a mass-spring oscillator.
🗣️ Conclusion and Additional Resources
In the concluding part of the video, Beck summarizes the key points discussed in the session and encourages the audience to utilize the available resources for further study and clarification. He mentions the AP daily videos and specific unit videos that could be beneficial for those needing extra help with experimental design and equipment selection. Beck also informs the audience about the location of the workbook within the AP classroom and reassures them that their feedback is valued and being reviewed, even though there is no direct method for responding. He signs off, reminding viewers about the next session with Kristin and encourages them to continue engaging and learning.
Mindmap
Keywords
💡Simple Harmonic Motion
💡Amplitude
💡Frequency
💡Period
💡Restoring Force
💡Spring Constant (k)
💡Equilibrium Position
💡Experimental Design
💡Feedback Form
💡AP Physics 1 Exam
Highlights
The session focuses on simple harmonic motion and incorporating experimental design based on student feedback.
Teacher Joshua Beck introduces himself and the purpose of the AP Physics 1 review session.
The concept of simple harmonic motion is explained with amplitude, frequency, and period.
The equation for the position of a simple harmonic oscillator is discussed, highlighting the role of amplitude, frequency, and time.
The requirement for an object to oscillate in simple harmonic motion is a net force opposite to the displacement.
Springs are ideal for simple harmonic motion due to their force increasing with displacement.
The method of measuring displacement from the equilibrium position simplifies the net force calculation.
The maximum force in simple harmonic motion is found at the amplitude points and is calculated by k times displacement.
The relationship between force and position is demonstrated, leading to the determination of the spring constant k.
The maximum acceleration and velocity points are identified as the equilibrium position and amplitude points, respectively.
The maximum kinetic and potential energies are found at the equilibrium position and amplitude points, respectively.
An experiment is proposed to determine the unknown spring constant of an ideal spring using the oscillation method.
The relationship between the period of oscillation, mass, and spring constant is derived and used to calculate k.
The effect of changing the mass or spring constant on the period is discussed using factor of change methodology.
The session concludes with the teacher encouraging students to use the feedback form and announcing the next session's instructor.
Transcripts
Browse More Related Video
AP Physics 1: Simple Harmonic Motion Review

2021 Live Review 3 | AP Physics 1 | Understanding Circular Motion and Gravitation

2021 Live Review 1 | AP Physics 1 | How to Understand Motion and Kinematics
AP Physics Workbook 6.L Sine function of SHM

2021 Live Review 3 | AP Physics C: Mechanics | Graphing Simple Harmonic Motion

8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion
5.0 / 5 (0 votes)
Thanks for rating: