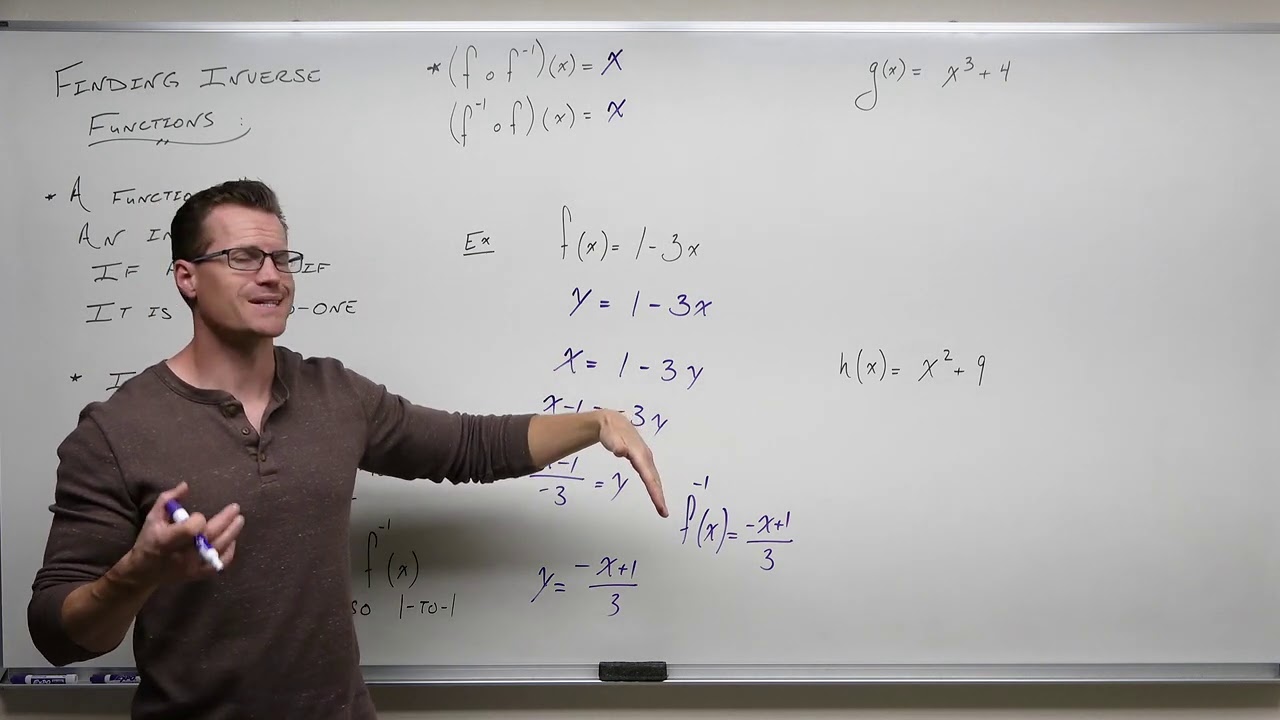Calculus 2 Lecture 6.2: Derivatives of Inverse Functions

Professor Leonard

22 Jan 201444:09

EducationalLearning

32 Likes 10 Comments

TLDRThe video transcript delves into the concept of inverse functions, emphasizing the importance of one-to-one relationships for the existence of inverses. It explains the process of finding inverses by switching x and y in the function and illustrates this with examples. The video also discusses the properties of inverse functions, such as their graphical representation as reflections across the line y=x and the continuity and differentiability of inverses when the original function possesses these properties. Additionally, it introduces a method for finding the derivative of an inverse function without explicitly identifying the inverse, using the original function's derivative and applying it to the inverse's evaluated point.

Takeaways

📚 The concept of inverse functions is introduced, explaining that for every one-to-one function, there exists an inverse.
🔄 A function and its inverse are graphically represented as reflections across the line y=x.
🎓 The horizontal line test is used to determine if a function is one-to-one, which is necessary for having an inverse.
🔢 To find the inverse of a function, you switch x and y in the function's equation and solve for y.
📈 When composing a function with its inverse, the result is the identity function, which outputs the original input value.
🌀 If a function is continuous on a certain domain, its inverse will also be continuous, but on a different domain which is the range of the original function.
📶 The differentiability of a function and its inverse are related; if a function is differentiable, its inverse is also differentiable.
🔍 To evaluate an inverse at a certain point without explicitly finding the inverse, use the definition of inverse functions and solve for the corresponding x value.
🧠 Finding the derivative of an inverse function at a specific point can be done using the formula G'(a) = 1 / F'(G(a)), where G is the inverse function of F.
📊 The process of finding the derivative of an inverse involves verifying the point is on the function, finding the derivative of the original function, and applying the inverse function's value to the derivative formula.
🤔 The script uses examples to illustrate the process of finding inverses and their derivatives, emphasizing the interplay between algebraic manipulation and understanding of function properties.

Q & A

What is the main topic of the transcript?
-The main topic of the transcript is the concept of inverse functions, their properties, how to find them, and how to determine if a function has an inverse.
What does it mean for a function to be one-to-one?
-A function is one-to-one if every input (x-value) has a unique output (y-value), meaning no two different inputs have the same output.
How can you determine if a function has an inverse?
-You can determine if a function has an inverse by checking if it passes the horizontal line test, which means no horizontal line intersects the graph of the function more than once.
What is the notation used for the inverse of a function?
-The notation used for the inverse of a function is F^(-1)(x) or f^(-1)(x), where the ^ (-1) denotes the inverse function.
What is the graphical relationship between a function and its inverse?
-The graph of a function and its inverse are reflections across the line y = x.
How does continuity affect the relationship between a function and its inverse?
-If a function F is continuous on a certain domain, then its inverse F^(-1) will also be continuous on a certain domain, specifically the range of F becomes the domain of F^(-1).
What is the process for finding the inverse of a given function?
-To find the inverse of a function, you switch the x and y variables, change the function name to y, and solve for y in terms of x.
How can you find the derivative of the inverse of a function without explicitly finding the inverse?
-You can find the derivative of the inverse by using the formula G'(a) = 1 / F'(G(a)), where G is the inverse function, F'(x) is the derivative of the original function, and G(a) is the value of the inverse function at a specific point a.
What is the significance of finding the derivative of an inverse function?
-Finding the derivative of an inverse function is important in calculus and other mathematical applications as it helps in understanding the slope or rate of change of the inverse function at a specific point.
How does the process of finding the inverse of a function relate to the concept of 'undoing' operations?
-The process of finding the inverse of a function is based on the concept of 'undoing' operations because the inverse function reverses the effect of the original function, effectively taking the output back to the input.

Outlines

00:00

📚 Introduction to Inverse Functions

This paragraph introduces the concept of inverse functions, emphasizing the importance of understanding their properties and behavior. It discusses the conditions for a function to have an inverse, specifically the 1-to-1 (one-to-one) requirement, meaning every input has a unique output. The concept of the horizontal line test is introduced to determine if a function is one-to-one. The paragraph also touches on the notation used for inverses and the idea that inverse functions 'undo' the action of their respective functions, akin to a child 'undoing' the cleaning done by their parent.

05:02

🔍 Finding Inverses and their Properties

The paragraph delves into the process of finding the inverse of a function by switching the x and y variables and solving for y. It provides a step-by-step example of finding the inverse of a given function and emphasizes the need to solve for y in terms of x. The paragraph also explains how to check if two functions are inverses by composing them and highlighting that the result should be the input variable x. Additionally, it briefly touches on the properties of inverse functions in calculus, such as continuity and differentiability, and how they relate to the original function.

10:07

📈 Graphing Inverse Functions

This section discusses the graphical representation of inverse functions, explaining that the graph of an inverse function is a reflection across the line y=x. It highlights that if the original function is one-to-one, its inverse will also be one-to-one, and vice versa. The paragraph also explains the relationship between the continuity of a function and its inverse, stating that if a function is continuous on a certain domain, its inverse will be continuous on the corresponding range. The concept is illustrated with a hypothetical example, reinforcing the idea that the range of the original function becomes the domain of its inverse.

15:09

🧠 Advanced Concepts in Inverse Functions

The paragraph presents more complex ideas about inverse functions, including the process of evaluating inverses at certain points without explicitly finding the inverse function. It introduces the concept of using conditional statements and algebraic manipulation to find the value of the inverse function at a given point. The paragraph challenges the audience with an example involving trigonometric functions, demonstrating the process of solving for x when f(x) equals a specific value. It emphasizes the importance of understanding the underlying concepts and being able to apply them to various scenarios.

20:10

📊 Derivatives of Inverse Functions

This section focuses on how to find the derivative of an inverse function at a specific point without finding the inverse function itself. It outlines a step-by-step process involving verifying that a point is on the function, finding the derivative of the original function, and then using the formula for the derivative of the inverse. The paragraph provides a clear example of finding the derivative of the inverse function at a given point, highlighting the mathematical process and the reasoning behind each step. It also introduces the notation G for the inverse function and explains how to apply the formula G'(x) = 1 / F'(G(x)) to find the derivative of the inverse at a specific point.

25:11

🔄 Inverses of Exponential and Logarithmic Functions

The paragraph concludes the discussion on inverse functions by connecting them to exponential and logarithmic functions. It establishes that exponential and logarithmic functions are inverses of each other, providing a logical transition to discussing exponential functions after covering logarithmic functions and inverses. The paragraph sets the stage for further exploration into the properties and applications of exponential functions in relation to their inverses, the logarithmic functions.

Mindmap

Keywords

💡Inverse Functions

Inverse functions are mathematical functions that 'undo' the effect of the original function. In the context of the video, this means that if you apply the function and then its inverse, you return to your starting value. For example, if a function F(x) transforms input x to output y, its inverse F^(-1)(y) would transform y back to x. The video explains that for a function to have an inverse, it must be one-to-one, meaning each input has a unique output.

💡One-to-One Functions

A one-to-one function is a type of function where each input value corresponds to exactly one output value. This property is crucial for a function to have an inverse because it ensures that the inverse function can uniquely determine the original input from any given output. The video emphasizes the importance of this characteristic for functions to have valid inverses.

💡Derivatives

Derivatives in calculus represent the rate of change or slope of a function at a particular point. The video discusses taking derivatives of inverse functions, which is a process that involves understanding how the rate of change of the inverse function relates to the original function. This is important in understanding the behavior of functions and their inverses around certain points.

💡Graphs

In mathematics, graphs are visual representations of functions where the x-axis represents inputs and the y-axis represents outputs. The video explains that the graph of a function and its inverse are related as reflections across the line y=x. This means that if you were to flip the graph of a function across the line y=x, you would get the graph of its inverse.

💡Composition of Functions

The composition of functions is the process of applying one function to the result of another function. In the context of inverse functions, the composition of a function and its inverse results in the identity function, which simply outputs the input. This property is used to verify that two functions are indeed inverses of each other.

💡Continuity

In mathematics, a function is said to be continuous if there are no abrupt changes, gaps, or breaks in its graph. The video discusses how if the original function F is continuous on a certain domain, then its inverse F^(-1) will also be continuous on a certain domain. This is important because continuous functions have well-defined properties that are preserved in their inverses.

💡Differentiability

A function is said to be differentiable if it has a derivative at every point in its domain. This means that the function has a well-defined slope at every point on its graph. The video explains that if the original function F is differentiable, then its inverse F^(-1) is also differentiable. This is significant because it allows us to analyze the rates of change and slopes of inverse functions as well.

💡Switching X and Y

Switching X and Y coordinates is a fundamental step in finding the inverse of a function. It involves interchanging the roles of the input (X) and output (Y) to find the inverse relationship. The video explains that to find the inverse of a function, you essentially switch the X and Y in the function's equation and then solve for Y to get the inverse function.

💡Horizontal Line Test

The horizontal line test is a graphical method to determine if a function is one-to-one. If any horizontal line intersects the graph of the function at more than one point, the function is not one-to-one and does not pass the test. This property is essential for a function to have an inverse, as each input must correspond to a unique output.

💡Algebraic Manipulation

Algebraic manipulation refers to the process of transforming and solving equations using algebraic techniques. In the context of the video, it is used to find the inverse of a function by manipulating the original function's equation to isolate the variable on the other side. This is crucial for understanding and solving for the inverse function.

Highlights

The introduction to inverse functions and their properties.

Explaining the concept of one-to-one functions and their relation to inverses.

The horizontal line test as a method to determine if a function is one-to-one.

How to find the inverse of a function by switching x and y variables.

The notation for inverse functions and how to denote them.

The method to check if two functions are inverses through composition.

The graphical relationship between a function and its inverse.

The impact of continuity on a function and its inverse.

How the domain and range switch between a function and its inverse.

The differentiability of a function and its inverse.

The process of evaluating inverses at certain points without explicitly finding the inverse function.

The method to find the derivative of an inverse function at a point without finding the inverse itself.

The application of the formula for the derivative of the inverse function G'(a) = 1/F'(G(a)).

Verification of a point being on the function before finding the inverse.

The concept of using the derivative to find the slope of the inverse function at a specific point.

Transcripts

Browse More Related Video

Derivatives of Inverse Functions

Finding Inverse Functions (Precalculus - College Algebra 51)

Introduction to Inverse Functions

Inverse Functions

Ch. 2.8 One-to-One Functions and their Inverses

Introduction to function inverses | Functions and their graphs | Algebra II | Khan Academy

Related Tags

Inverse Functions Derivatives One-to-One Horizontal Line Test Function Composition Algebraic Techniques Calculus Concepts Trigonometric Functions Inverse Relationships Exponential Logarithmic