Ch. 2.8 One-to-One Functions and their Inverses
TLDRThis educational video script introduces the concept of one-to-one functions and their inverses. It explains that a one-to-one function has a unique output for each input, using the horizontal line test to identify such functions. The script clarifies that the inverse function, denoted by f^(-1)(x), is not the reciprocal but a function that reverses the original's action. It demonstrates how to graph inverse functions by swapping x and y coordinates and algebraically finding them by swapping variables and solving for the new variable. The importance of one-to-one functions for invertibility is emphasized, and examples illustrate the process of finding inverses and determining when a function is not invertible due to non-unique outputs.
Takeaways
- 😀 A one-to-one function (notated as 1-1) ensures that each unique input has a unique output, with no two different inputs producing the same output.
- 📏 The horizontal line test can be used to determine if a function is one-to-one; if a horizontal line crosses the graph more than once, the function is not one-to-one.
- 🔄 The concept of inverse functions is introduced for one-to-one functions, where the notation f^(-1)(x) represents the inverse of function f(x).
- 🚫 It's important to differentiate between the inverse function (f^(-1)(x)) and the reciprocal function (1/f(x)), as they are not the same.
- 🔄 The inverse function essentially reverses the roles of inputs and outputs, taking the outputs of the original function as its inputs and vice versa.
- 🛫 The process of finding an inverse function algebraically involves swapping x and y in the original function's equation and solving for the new y, which then becomes f^(-1)(x).
- 📊 When graphing an inverse function, the x and y values of the original function are swapped, resulting in a reflection across the line y=x.
- ❌ If a function cannot be expressed as a single function when attempting to find its inverse, it indicates that the original function is not one-to-one and thus not invertible.
- 📚 The script provides examples of finding inverse functions algebraically, including handling cases where the inverse cannot be expressed as a single function due to the original function not being one-to-one.
- 📈 The script also discusses determining the inverse of a function using a table of values, highlighting the process of tracing inputs and outputs through multiple functions and their inverses.
- 📉 The importance of one-to-one functions in calculus and their relevance to the rest of the semester's material is emphasized, suggesting that understanding these concepts will be beneficial for further studies.
Q & A
What is a one-to-one function?
-A one-to-one function, denoted as 1-1, is a function where each input has a unique output. No two different inputs can produce the same output.
Why is the function f(x) = x^2 not one-to-one?
-The function f(x) = x^2 is not one-to-one because it does not satisfy the condition that different inputs must have different outputs. For example, f(2) and f(-2) both yield the same output of 4.
What is the horizontal line test and how does it relate to one-to-one functions?
-The horizontal line test is a graphical method to determine if a function is one-to-one. If a horizontal line drawn anywhere on the graph of the function crosses it more than once, the function is not one-to-one.
What is the notation for the inverse of a function?
-The notation for the inverse of a function f is f^(-1)(x), which is read as 'f inverse of x'.
How is the inverse function related to the original function?
-The inverse function essentially reverses the process of the original function. It takes the outputs of the original function and uses them as inputs, and vice versa.
What is the difference between f^(-1)(x) and 1/f(x)?
-f^(-1)(x) represents the inverse function, which is a completely different function that reverses the original function's mapping. On the other hand, 1/f(x) is an algebraic representation of the reciprocal function, which is not the same as the inverse function.
How can you determine if a function has an inverse?
-A function has an inverse if it is one-to-one. This can be checked using the horizontal line test or by ensuring that no two different inputs produce the same output.
How do you graph the inverse function of a given function?
-To graph the inverse function, you take the x and y values of the original function and swap them. This results in a reflection of the graph across the line y = x.
What happens to the domain and range of a function when you find its inverse?
-When finding the inverse function, the domain and range of the original function switch places. The original range becomes the domain of the inverse function, and the original domain becomes its range.
How do you find the inverse function algebraically?
-To find the inverse function algebraically, you start by replacing f(x) with y, then swap all x's with y's and y's with x's. After that, solve for y and replace y with f^(-1)(x) to get the inverse function.
Why can't a quadratic function like f(x) = (1/2)x^2 + 2 be inverted to a single function?
-A quadratic function like f(x) = (1/2)x^2 + 2 cannot be inverted to a single function because it is not one-to-one. When trying to find the inverse, you end up with two expressions, one for the positive case and one for the negative case, indicating that the original function does not pass the horizontal line test.
What does it mean if a function is not one-to-one?
-If a function is not one-to-one, it means that there are at least two different inputs that produce the same output. Such a function does not have an inverse function because the inverse would not be a function itself, as it would not pass the vertical line test.
How can you find composite functions involving inverses using a table of values?
-To find composite functions involving inverses using a table of values, you follow the order of operations, substituting inputs into functions and inverses as needed, and then finding the corresponding outputs. If at any point you encounter the same output for different inputs, it indicates that the inverse is not a function.
Outlines
📚 Introduction to One-to-One Functions and Their Inverses
This paragraph introduces the concept of one-to-one functions, denoted as 1-1, which are functions where each unique input corresponds to a unique output. The instructor uses the example of f(x) = x^2 to illustrate that it is not a one-to-one function due to the same output (four) being produced by two different inputs (two and negative two). The horizontal line test is explained as a method to determine if a function is one-to-one, where if a horizontal line intersects the graph more than once, the function is not one-to-one. The importance of one-to-one functions is emphasized as they possess inverse functions, which are denoted by f^(-1)(x) and are not to be confused with the reciprocal function (1/f(x)). The inverse function is explained as a process that takes the outputs of the original function and uses them as inputs, essentially reversing the direction of the mapping from input to output.
📈 Graphing Inverse Functions and Understanding Their Algebraic Representation
The paragraph delves into the process of graphing inverse functions by swapping the x and y values of the original function's graph, resulting in a reflection across the line y=x. The instructor uses a generic function and its graph to demonstrate this concept, explaining that points on the line y=x remain unchanged when the inverse function is applied because swapping x and y yields the same point. The algebraic method of finding the inverse function is also discussed, involving replacing f(x) with y, swapping x and y throughout the equation, and solving for y to obtain the inverse function, which is then denoted as f^(-1)(x). An example is provided to illustrate the algebraic process of finding the inverse of a given function.
🔍 Analyzing the Invertibility of Functions Through Algebraic Manipulation
This section discusses the challenges of finding inverse functions algebraically, particularly when the original function is not one-to-one. The instructor demonstrates this with an example where attempting to find the inverse of f(x) = (1/2)x^2 + 2 leads to two separate expressions due to the square root operation, indicating that the original function is not invertible as it does not satisfy the one-to-one condition. The concept is reinforced by explaining that if a function cannot be represented by a single expression for its inverse, it is not one-to-one and therefore not invertible. The importance of the vertical line test in determining if a function's graph represents a valid inverse function is also highlighted.
📝 Applying Function Inverses Through Tables and Understanding Their Limitations
The final paragraph focuses on using tables of values to understand function inverses and their limitations. The instructor provides a table with inputs and outputs for different functions and demonstrates how to find composite functions involving inverses. However, when attempting to find the inverse of a function that is not one-to-one, it is shown that multiple inputs can correspond to the same output, indicating that the inverse is not well-defined and the function is not one-to-one. This leads to the conclusion that not all functions have inverses, and the ability to find a single-valued inverse is contingent upon the original function being one-to-one. The instructor also encourages students to take notes on the upcoming chapter, emphasizing its importance for future studies.
Mindmap
Keywords
💡One-to-One Functions
💡Horizontal Line Test
💡Inverse Functions
💡Function Notation
💡Domain and Range
💡Reflection Across the Line y=x
💡Algebraic Manipulation
💡Table of Values
💡Composite Functions
💡Non-Invertible Functions
Highlights
Introduction to chapter 2.8 on one-to-one functions and their inverses.
Definition of a one-to-one function and its notation.
Explanation of the uniqueness of outputs in one-to-one functions.
Illustration of why f(x) = x squared is not a one-to-one function.
Introduction of the horizontal line test for identifying one-to-one functions.
Importance of one-to-one functions in relation to inverse functions.
Clarification on the notation and concept of inverse functions.
Differentiation between inverse functions and reciprocal functions.
Explanation of the process of finding an inverse function using algebraic notation.
Graphical representation of inverse functions and the concept of reflection across the line y=x.
Process of graphing an inverse function by swapping x and y values.
Algebraic method for finding the inverse function by swapping variables.
Example of finding the inverse function for a given algebraic expression.
Demonstration of why a quadratic function cannot have an inverse function.
Use of tables of values to understand inverse functions.
Analysis of composite functions and their inverses using tables of values.
Conclusion on the importance of chapter three for future calculus studies.
Transcripts
Browse More Related Video
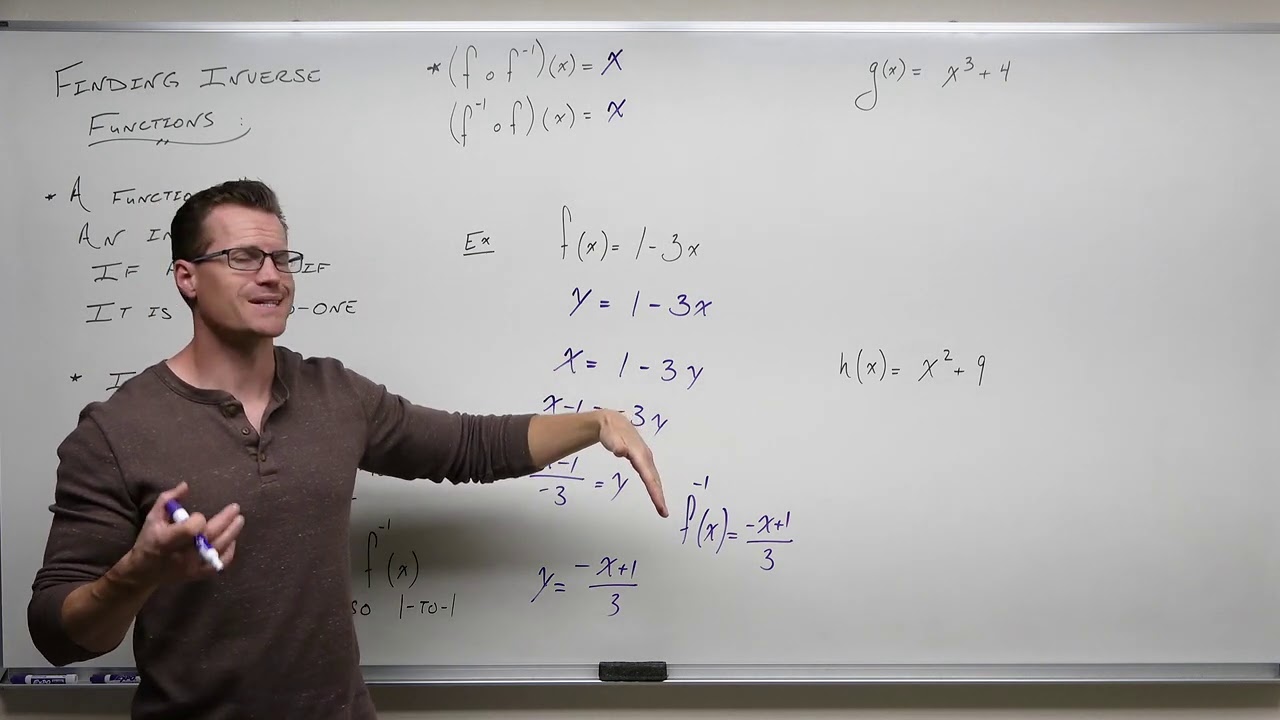
Finding Inverse Functions (Precalculus - College Algebra 51)

One to One Functions (Precalculus - College Algebra 50)

Inverse Functions

Introduction to Functions (Precalculus - College Algebra 2)

Inverse Functions - Domain & range- With Fractions, Square Roots, & Graphs

Introduction to function inverses | Functions and their graphs | Algebra II | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: