Inverse Functions
TLDRThe video script delves into the concept of inverse relations and functions, a crucial topic in algebra and beyond. It begins with a graphical approach, illustrating how to plot the inverse of a function by swapping x and y values, and emphasizes the symmetry with respect to the line y=x. Examples include graphing a parabola and a linear function, highlighting the vertical line test for determining if an inverse is a function. The script then introduces algebraic methods for finding inverse functions, using horizontal line tests and solving for y. It also covers the formal definition of inverses through function composition, ensuring they 'undo' each other. The lesson is capped with examples that demonstrate finding and verifying inverses, reinforcing the importance of understanding these mathematical relationships.
Takeaways
- 📈 The concept of inverse relations and functions is revisited because of its importance throughout the year.
- 📚 Inverse relations can be understood graphically by switching the x and y values of a function's graph, which also switches the domain and range.
- 🔍 A function and its inverse are symmetric with respect to the line y = x, as demonstrated through the example of f(x) = x^2 - 1.
- 🚫 Not all inverses are functions; an inverse must pass the vertical line test to be considered a function.
- 📐 The example of f(x) = 2x - 1 shows that its inverse is a function, as it passes the horizontal line test.
- 🔑 The notation for the inverse of a function f is f^(-1)(x), which is not the same as 1/f(x).
- ✅ A function must pass the horizontal line test to have an inverse that is also a function, meaning it is one-to-one.
- 🔍 Algebraically finding an inverse involves checking if the function is one-to-one, switching x and y, and solving for y.
- 📘 Restrictions on the domain of the original function may apply to the domain of the inverse function, as seen with f(x) = x / (2x - 1).
- 📉 The example of f(x) = 2√(x - 1) shows how to find the inverse function and its restricted domain.
- 🔄 The formal definition of inverse functions is that f(f^(-1)(x)) and f^(-1)(f(x)) both equal x, indicating that the functions undo each other's effects.
Q & A
What is the graphical representation of an inverse function?
-Graphically, an inverse function is represented by switching the x and y values of the original function's graph. If the original function is a graph that passes the horizontal line test, its inverse will be symmetric to the line y = x.
How does the domain and range switch when finding the inverse of a function?
-When finding the inverse of a function, the domain and range of the original function are switched. This means that the domain of the original function becomes the range of the inverse function, and vice versa.
What is the condition for a function and its inverse to be symmetric to the line y = x?
-A function and its inverse are symmetric to the line y = x if the original function passes the horizontal line test, indicating that each x-value corresponds to exactly one y-value, making it a one-to-one function.
Why does the inverse of a parabola not pass the vertical line test?
-The inverse of a parabola does not pass the vertical line test because a parabola, when reflected over the line y = x, does not have a unique output for each input, which violates the definition of a function where each input must correspond to exactly one output.
What does the notation f^(-1)(x) represent in mathematics?
-The notation f^(-1)(x) represents the inverse of the function f(x). It indicates that f^(-1) is the function that reverses the effect of f, provided that f is a one-to-one function and has an inverse.
How can you determine if a function has an inverse that is also a function?
-To determine if a function has an inverse that is also a function, you must check if the original function passes the horizontal line test. If no horizontal line intersects the graph at more than one point, the function is one-to-one and has an inverse that is a function.
What is the algebraic process to find the inverse of a function?
-To find the inverse of a function algebraically, you first replace the function notation f(x) with y. Then, swap the x's and y's, and solve the resulting equation for y. The expression for y that you obtain is the inverse function, denoted as f^(-1)(x).
What restrictions might there be on the domain of an inverse function?
-The domain of an inverse function may be restricted to exclude values that do not satisfy the original function's one-to-one condition. For example, if the original function has a domain where certain x-values correspond to the same y-value, these x-values would not be included in the domain of the inverse function.
How can you verify if two functions are inverses of each other?
-To verify if two functions are inverses, you can compose them, meaning you substitute one function into the other. If the composition of f(g(x)) and g(f(x)) both result in x, then the functions are inverses of each other.
Can the inverse of a function be the same as the original function?
-Yes, it is possible for the inverse of a function to be the same as the original function. This occurs when the function is symmetric with respect to the line y = x and satisfies the conditions of being a one-to-one function.
Outlines
📚 Introduction to Inverse Relations and Functions
This paragraph introduces the topic of inverse relations and functions, a concept previously encountered in algebra 2. The speaker emphasizes its importance and begins with a graphical approach to understanding inverses. A function's graph can be inverted by swapping the x and y values, which also swaps the domain and range. The inverse of a function is symmetrical to the original function with respect to the line y=x. An example is given with the function f(x) = (x-1)^2 + 2, demonstrating how to graph the original function and its inverse. It's noted that while every function has an inverse, not every inverse is a function, as shown by the failure of the inverse to pass the vertical line test.
📈 Graphical Representation and Horizontal Line Test
The speaker continues with the graphical representation of inverse functions, using the example of the line f(x) = 2x - 1 and its inverse. The process involves switching the x and y coordinates to find the inverse's graph. It's explained that for a graph to have an inverse that is a function, it must pass the horizontal line test, meaning no horizontal line should intersect the graph at more than one point. The concept of one-to-one functions is introduced, where each x value corresponds to exactly one y value, and vice versa for the inverse.
🔍 Algebraic Inverse Functions and Domain Restrictions
The discussion shifts to finding inverse functions algebraically. The process involves checking if the function is one-to-one using the horizontal line test, then swapping x and y, and solving for y to find the inverse. An example is given with f(x) = x / (2x - 1), where the graph passes the horizontal line test, indicating the existence of an inverse function. The domain and range of the original function are considered when finding restrictions for the inverse. The example concludes with finding the inverse function and noting the domain restrictions, highlighting the switch between domain and range for the inverse function.
🔢 Verifying Inverse Functions and Composition
The final paragraph delves into the formal definition of inverse functions, where f(f(x)) and g(x) are inverses if their composition results in the identity function (x). The speaker provides a method to verify if two functions are inverses by composing them and checking if the result is x. Examples are given with f(x) = 3x^2 + 7 and g(x) = sqrt(x - 7) / 3, showing the step-by-step process of composition in both directions to confirm they are indeed inverses. Another example with f(x) = 2/3x + 2 and g(x) = 3/2(x - 3) is used to further illustrate the verification process, concluding that these functions are also inverses.
Mindmap
Keywords
💡Inverse Relations
💡Function
💡Domain and Range
💡Symmetric
💡Vertical Line Test
💡Horizontal Line Test
💡One-to-One
💡Algebraic Inverse
💡Composite Functions
💡Restrictions on the Domain
Highlights
Introduction to inverse relations and functions, a revisit from algebra 2.
Graphical representation of functions and their inverses by switching x and y values.
Explanation of how switching x and y implies domain and range are switched.
Symmetry of a function and its inverse to the line y=x.
Example graphing of f(x) = x^2 - 1 and its inverse.
Demonstration that the inverse of a parabola is not always a function due to failure of the vertical line test.
Graphing the line f(x) = 2x - 1 and its inverse, showing it as a function.
Introduction of inverse notation f^(-1)(x) and its distinction from 1/f(x).
Requirement for a graph to have an inverse function: passing the horizontal line test.
Concept of one-to-one functions and their relation to inverse functions.
Algebraic method to find inverse functions by checking if they are one-to-one and solving for y.
Example of determining if f(x) = x / (2x - 1) has an inverse function and finding its restrictions.
Unique case where a function and its inverse are the same due to domain and range switching.
Graphing and inverse function finding for f(x) = 2√(x - 1) with domain restrictions.
Explanation of the formal definition of inverse functions and their composition.
Verification of inverse functions through composition examples.
Summary of the process to determine and find inverse functions, including restrictions and compositions.
Transcripts
Browse More Related Video

Introduction to Inverse Functions

Inverse Functions - Domain & range- With Fractions, Square Roots, & Graphs

12 - What are Inverse Functions? (Part 1) - Find the Inverse of a Function & Graph
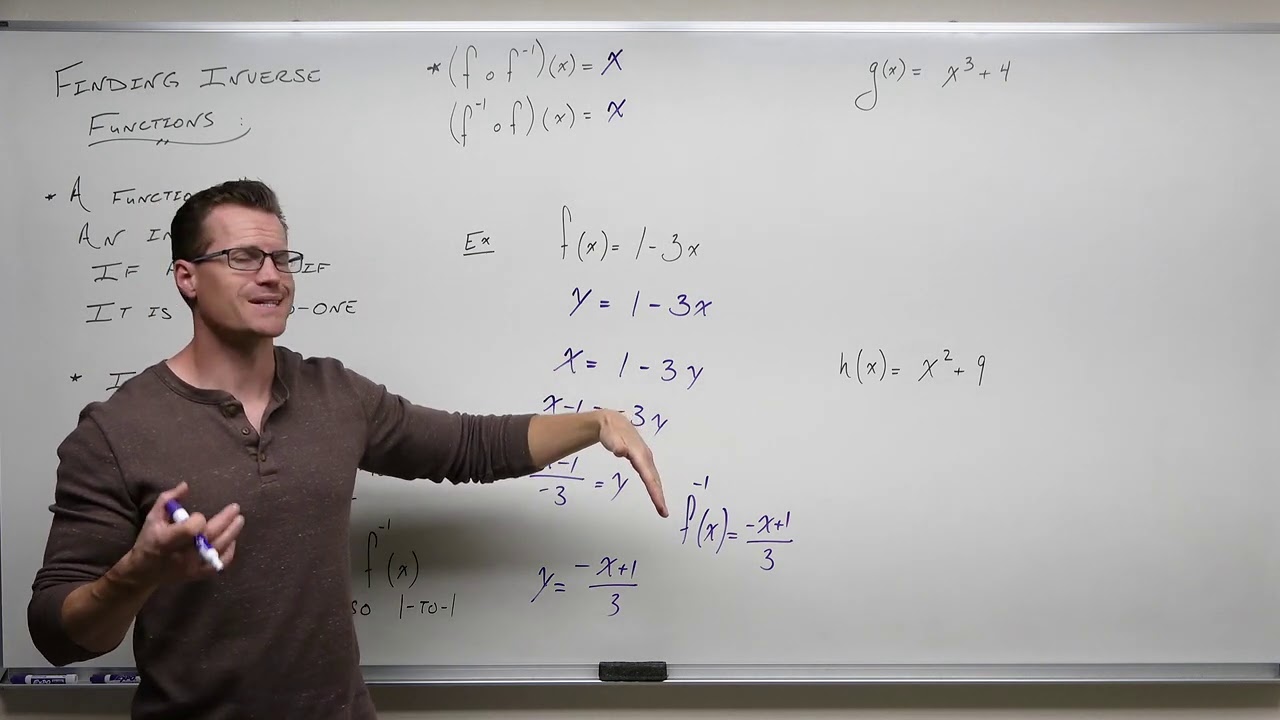
Finding Inverse Functions (Precalculus - College Algebra 51)

Ch. 2.8 One-to-One Functions and their Inverses
Calculus 2 Lecture 6.2: Derivatives of Inverse Functions
5.0 / 5 (0 votes)
Thanks for rating: