AP Physics Workbook 8.B Electric Force
TLDRThis transcript from an AP Physics workbook tutorial, Unit Eight, delves into electric charge and forces. It explains how like charges repel and introduces Coulomb's Law, detailing its formula and significance in calculating the magnitude of electric forces between charges. The tutorial also addresses a common misconception about the direction of electric forces and emphasizes that Coulomb's Law provides magnitude, with direction determined by the charge's sign. A problem is presented on placing a third charge to achieve a net force of zero between two charges, with a detailed explanation of the solution.
Takeaways
- 📌 The scenario involves understanding electric forces between two like charges and their vector representation.
- 🔋 Charges of the same type repel each other, as demonstrated by the forces between two identical charges.
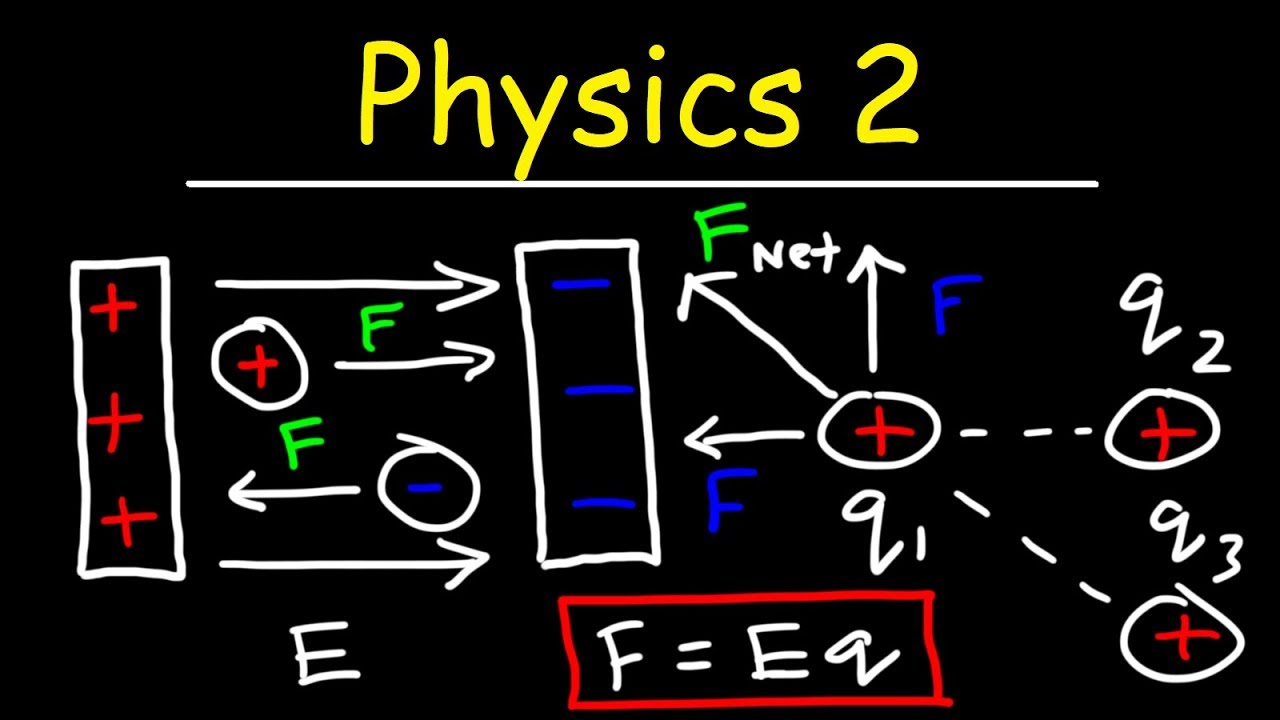
- 📈 The magnitude of the electric force can be calculated using Coulomb's Law, expressed as F = k * (q1 * q2) / r^2, where k is Coulomb's constant, q1 and q2 are the charges, and r is the distance between them.
- 🧲 The direction of the static electric force is always along the line joining two charges, and it depends on the sign of the charges whether the force is attractive or repulsive.
- 🔄 When one charge is multiplied by a factor (e.g., 5q), the force also increases proportionally, demonstrating a direct linear relationship between charge and force.
- 📐 To achieve a net electric force of zero between two charges, a third charge of opposite sign can be placed at a specific position along the line joining the two original charges.
- 🤔 The position of the third charge (negative 2q) depends on the magnitudes of the original charges and is placed closer to the weaker charge (positive q) to balance the forces.
- 🚫 The script corrects a misconception about the direction of electric force; the sign of the charge (positive or negative) determines the direction, not the mere presence of a positive or negative value.
- 📚 Coulomb's Law provides the magnitude of the force but does not dictate the direction; the direction is inferred from whether the force is attractive or repulsive based on the signs of the charges involved.
- 🌟 In calculations, it is common to use the absolute value of charges and determine the direction separately, based on the attractive or repulsive nature of the force.
- 📝 The key to understanding electric forces lies in grasping the relationship between charge, the magnitude of force, and the directionality as governed by Coulomb's Law.
Q & A
What is the main topic of Unit Eight in the AP Physics workbook?
-The main topic of Unit Eight is electric charge and electric forces.
How do two charges of the same type interact according to the scenario described?
-Two charges of the same type will repel each other.
What is Coulomb's Law and how is it applied in this context?
-Coulomb's Law states that the magnitude of the electric force between two point charges is equal to the product of the charges divided by the square of the distance between them, multiplied by the constant k. It is used to calculate the force between two charges and to determine the direction of the force along the line joining the charges.
What is the relationship between the magnitude of the charge and the electric force?
-The magnitude of the charge has a linear direct relationship with the electric force, meaning that if the charge is increased, the force will increase proportionally.
How does the scenario change when one of the charges is increased to 5q?
-When one of the charges is increased to 5q, the force between the charges also increases by a factor of 5, becoming 15 units.
What is the purpose of the third charge (negative q) in the problem?
-The purpose of the third charge (negative q) is to find a position where it can be placed such that the net electric force on it from the other two charges is zero.
Where should the third charge (negative q) be placed to achieve a net force of zero?
-The third charge should be placed on the perpendicular bisector of the line joining the two original charges, closer to the positive charge, to achieve a net force of zero.
What is the common misconception about the direction of electric force according to the argumentation section?
-The common misconception is that the positive direction is always to the right and that the force between charges depends on the signs of the charges (positive or negative), which is incorrect. Coulomb's Law gives the magnitude of the force, and the direction is determined by the charge system used.
How should one correctly interpret the magnitude and direction of the force from Coulomb's Law?
-One should interpret the magnitude of the force from the absolute value of the product of the charges and the inverse square of the distance between them. The direction of the force is along the line joining the two charges, with like charges repelling each other and opposite charges attracting each other.
What is the significance of understanding the direction of electric forces in physics?
-Understanding the direction of electric forces is crucial for predicting the behavior of charged particles, designing electrical circuits, and comprehending fundamental physical phenomena such as electrostatics and electromagnetism.
Why is it important to consider both magnitude and direction when calculating electric forces?
-Both magnitude and direction are essential when calculating electric forces because they determine the overall effect of the force on charged particles, which can lead to attraction or repulsion and influence the trajectory and energy of the particles.
Outlines
📚 Introduction to Electric Forces and Charges
This paragraph introduces the topic of the tutorial, which is Unit Eight on Electric, Charge, and Electric Forces. It sets the scene for the exploration of the electric force between two like charges, explaining that they will repel each other. The scenario involves two charges of the same strength, and the task is to draw vectors representing the forces between them. The paragraph also touches on the concept of the electric field and mentions Coulomb's Law as the governing principle for calculating the magnitude of the forces between charges.
🔢 Analysis of Coulomb's Law and Electric Forces
This paragraph delves deeper into the mathematical aspect of Coulomb's Law, which is used to determine the magnitude of the electric force between two charges. It explains that the force is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. The tutorial corrects a misconception about the direction of the electric force, emphasizing that the direction is along the line joining the two charges and depends on their signs. It also addresses the relationship between the magnitude of the charge and the force, stating that there is a linear direct relationship between them.
🤔 Problem Solving and电荷平衡
The paragraph presents a problem-solving scenario where a third charge (negative q) is to be placed between two like charges to achieve a net electric force of zero. It explains the solution, which involves placing the negative charge on a line equidistant from the two positive charges to balance the forces. The paragraph also critiques a statement that misunderstands the direction and nature of the electric force between charges, clarifying the correct interpretation of Coulomb's Law. It reiterates the importance of understanding the direction of the electric force and how to calculate it using Coulomb's Law.
📝 Summary of Coulomb's Law and its Applications
In conclusion, this paragraph summarizes the key points about Coulomb's Law and its application in understanding electric forces. It reiterates that Coulomb's Law provides the magnitude of the force and that the direction is determined by the charge system. The summary emphasizes the importance of considering the sign of the charges when calculating the force and determining the direction. It also provides guidance on how to approach problems involving electric forces and charges, reinforcing the principles learned throughout the tutorial.
Mindmap
Keywords
💡Electric charge
💡Electric force
💡Coulomb's law
💡Vector
💡Repulsion
💡Electric field
💡Net electric force
💡Attraction
💡Charge magnitude
💡Direction
💡Positive and negative charges
Highlights
The scenario involves understanding electric forces and charges, specifically when two like charges interact.
In the given situation, two charges of the same type repel each other, as indicated by the force vectors F12 and F21.
The electric field is represented by the force vectors pointing away from charges of the same sign.
Coulomb's Law is introduced as the fundamental principle governing the interaction between charges, expressed as k*q*Q/r^2.
The direction of the static electric force is always along the line joining two charges, which is crucial for visualizing and calculating forces.
The magnitude of the force between two charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them.
When one charge is multiplied by a factor (e.g., 5q), the force it exerts also increases by that same factor, demonstrating a linear relationship.
The electric field is a vector quantity, and its direction is determined by the nature of the charge (positive or negative).
A third charge (negative 2q) can be placed between two like charges to neutralize the net electric force, but its position is critical and depends on the magnitudes of the original charges.
The net force on the third charge would be zero if placed directly on the line joining the two original charges, at a position where the forces from the two charges balance each other.
The explanation of the electric force direction is clarified by the alignment of forces along the line joining charges and the concept of repulsion or attraction based on charge polarity.
The argumentation section critiques a statement that misinterprets the direction of electric force and the interaction between charges of different signs.
It is clarified that the positive direction does not have to be to the right, and the coordinate system can be defined in various ways.
Coulomb's Law provides the magnitude of the force, and the direction must be determined separately based on the charges' signs.
The correct interpretation of Coulomb's Law is that it gives the magnitude of the electric force, and the direction is along the line joining the charges, with forces being attractive or repulsive depending on the charge signs.
The summary of Coulomb's Law in the transcript emphasizes the importance of understanding both the magnitude and direction of the electric force for problem-solving.
The practical application of this knowledge is demonstrated through the problem-solving process, showing how to calculate and visualize electric forces in a given scenario.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: