What is the Electric Field? How do Electric Forces Work?
TLDRThe video script discusses the concept of electric fields, their origin from charged particles, and the forces they exert on other charges. It explains the symmetry between electric and gravitational forces, and introduces Coulomb's law, which describes the force between charges. The script also delves into the electric field of a point charge and how it radiates outward, influencing other charges. The importance of electric fields in physics and their applications in various scenarios, such as electromagnetic waves, are highlighted. The content is delivered through a detailed explanation complemented by illustrative examples and analogies, emphasizing the practical significance of understanding electric fields.
Takeaways
- 📌 The concept of electric fields is introduced as an invisible vector field that surrounds charged particles, similar to the gravitational force field around massive objects.
- 🔋 Charges naturally produce electric fields, and these fields can be represented with arrows indicating direction and intensity.
- 💥 Like charges repel each other, while opposite charges attract, and this interaction is governed by Coulomb's Law, which is analogous to the gravitational force law.
- 🤔 The question of how charges 'know' about each other's presence is explored, highlighting the fundamental nature of forces in physics that cannot be fully explained, only observed and described.
- 🌐 The electric field of a point charge is radially directed and decreases in intensity with distance, following an inverse square law similar to gravitational fields.
- 🔧 The direction of the electric field is determined by the nature of the charge: positive charges create fields that point away from them, while negative charges create fields that point towards them.
- 📈 The force experienced by a charged particle in an electric field is directly related to the charge's magnitude and the strength and direction of the electric field at the particle's location.
- 🔍 The script emphasizes the importance of visualizing electric fields and understanding how charges move within these fields, as this knowledge is crucial for problem-solving in physics.
- 🧠 The concept of superposition is mentioned, where the total electric field at a point is the vector sum of the electric fields due to individual charges.
- 📚 The script concludes with a reminder that understanding electric fields is foundational for further studies in physics, including electromagnetic waves and their role in everyday life.
Q & A
What is the main topic discussed in the script?
-The main topic discussed in the script is the concept of the electric field, specifically focusing on the electric field of a point charge and how it relates to the Coulomb force.
How does the Coulomb force law relate to the electric field?
-The Coulomb force law describes the force between two charges, and it is similar to the gravitational force law. The electric field is an alternative way of explaining the interaction between charges, where the electric field is generated by the charges and interacts with other charges to produce a force, which is consistent with the Coulomb force law.
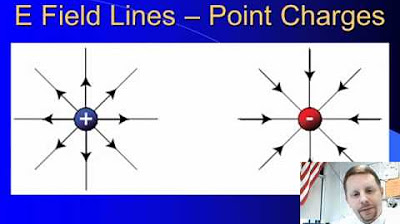
What is the direction of the electric field lines around a positive charge?
-The electric field lines around a positive charge radiate outward from the charge.
What is the direction of the electric field lines around a negative charge?
-The electric field lines around a negative charge point towards the charge.
How do positive and negative charges interact in an electric field?
-Opposite charges (positive and negative) attract each other in an electric field, while like charges (positive-positive or negative-negative) repel each other.
What is the formula for the electric field due to a point charge?
-The electric field (E) due to a point charge (Q) is given by the formula E = k * Q / r^2, where k is the electrostatic constant (also known as Coulomb's constant), Q is the charge, and r is the distance from the charge.
How does the electric field strength change with distance from the charge?
-The electric field strength decreases with the square of the distance from the charge, following the inverse square law.
What is the role of the electric field in understanding the force between charges?
-The electric field provides a framework to understand and predict how charges will interact with each other. It helps to visualize and calculate the forces between charges without directly calculating the interaction of every individual pair of charges.
How does the superposition principle apply to electric fields?
-The superposition principle states that the total electric field at a point is the vector sum of the electric fields produced by each charge at that point. This allows us to calculate the resultant electric field due to multiple charges by summing the individual contributions from each charge.
What is the significance of the electric field in physics and engineering?
-The electric field is fundamental to understanding electromagnetic interactions and is crucial in many areas of physics and engineering. It is used to describe the behavior of charges, design electrical circuits, and study phenomena like electromagnetic waves.
Outlines
📘 Introduction to Electric Fields
The paragraph introduces the concept of electric fields, setting the stage for a deeper understanding of this fundamental aspect of physics. It begins by discussing the Coulomb force between charges, highlighting the similarities between electric and gravitational forces. The speaker emphasizes the importance of observing and describing physical phenomena before attempting to understand the underlying reasons for their behavior. The paragraph sets a foundation for exploring how charges interact through the electric field, a concept that will be developed and applied throughout the lecture.
🔋 The Electric Field: A Vector Field
This paragraph delves into the nature of the electric field as a vector field, emphasizing its invisibility and the way it is represented with arrows. The electric field is likened to a gravitational field, with charges causing a curvature in space-time similar to how a massive object influences gravity. The speaker explains that every charged particle creates an electric field and that other charged particles will move along these field lines, demonstrating the self-consistency of physics. The paragraph also touches on the idea of electric field lines and their direction, providing a visual and intuitive understanding of electric fields.
🤔 The Mystery of Interaction through Electric Fields
The speaker poses a philosophical question about how charges 'know' to interact with each other through electric fields. While acknowledging that we don't have a fundamental understanding of this interaction, the speaker suggests that the concept of the electric field is a useful mathematical construct. This construct helps predict how charged particles will behave, even though we can't observe the electric field directly. The paragraph also compares the electric field to the curvature of space-time in gravity, indicating a potential deeper connection between these forces.
🌐 Visualizing Electric Fields
This paragraph describes how to visually represent electric fields, particularly around point charges. The speaker explains that electric fields radiate symmetrically from positive charges and terminate at negative charges, creating a pattern that can be drawn with arrows to indicate direction. The paragraph emphasizes the importance of understanding these visual representations, as they help in predicting the motion of charged particles within the field. The speaker also clarifies that while the electric field is a mathematical construct, it is incredibly useful for solving real-world physics problems.
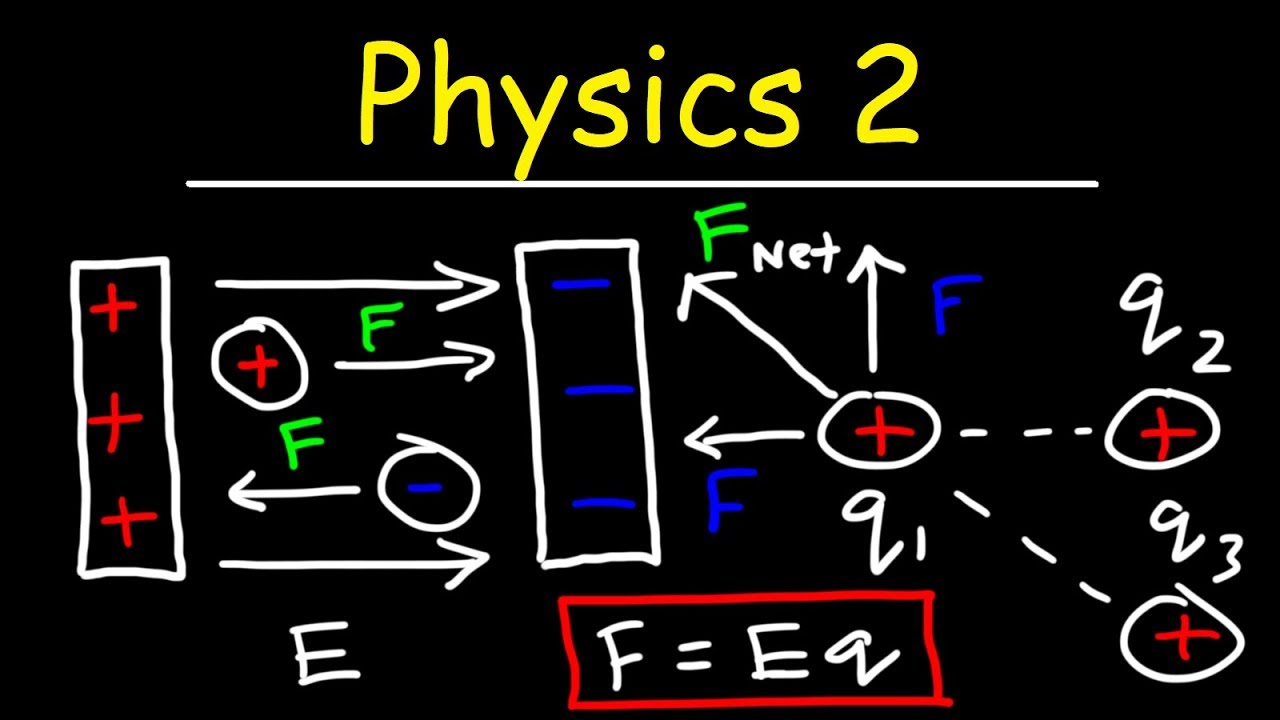
🎯 The Behavior of Charges in Electric Fields
The speaker elaborates on how charges interact with electric fields. Positive charges are said to follow the direction of the electric field lines, while negative charges move in the opposite direction. This behavior is consistent with Coulomb's law, which describes the forces between charges. The paragraph reinforces the concept that the electric field is responsible for the motion of charges and that this motion is predictable and consistent with established physical laws. The speaker also introduces the idea that the direction of the electric field dictates the direction of the force acting on a charge placed within it.
📚 Equations of Electric Fields
The paragraph transitions into the mathematical representation of electric fields. The speaker presents the equation for the force on a charge placed in an electric field, highlighting that the force is in the same direction as the electric field. The paragraph then rearranges this equation to solve for the electric field itself, providing the equation for the electric field due to a point charge. The speaker emphasizes the importance of understanding these equations, as they allow for the calculation of electric fields and the forces on charges within those fields. The equations are shown to be consistent with Coulomb's law, reinforcing the connection between electric fields and the forces between charges.
🔍 Analyzing Electric Fields of Multiple Charges
The speaker discusses the concept of superposition in relation to electric fields. When multiple charges are present, each generates an electric field, and the resultant electric field at any point is the vector sum of the individual fields. The paragraph explains that while the electric fields from individual charges radiate outward, the actual electric field at a point is the combined effect of all charges. The speaker emphasizes the importance of considering the vector nature of electric fields when calculating the resultant field, as this will determine the overall direction and magnitude of the electric field at any given point.
📝 Solving Problems with Electric Fields
The speaker provides a step-by-step approach to solving problems involving electric fields. The paragraph outlines the process of calculating the electric field at a point due to multiple charges, using the principle of superposition. The speaker also discusses the importance of drawing and analyzing diagrams when dealing with electric fields, as this aids in visualizing the interactions between charges and their fields. The paragraph concludes with a reminder that the electric field equations must be applied consistently and with an understanding of their physical implications to arrive at correct solutions.
Mindmap
Keywords
💡Electric Field
💡Coulomb's Law
💡Point Charge
💡Vector Field
💡Charge
💡Superposition
💡Permittivity of Free Space
💡Test Charge
💡Electric Field Lines
💡Gravitational Force
Highlights
Introduction to the electric field concept and its relation to charged particles
Explanation of the Coulomb force and its similarity to gravitational force
Discussion on the observation and description of physical phenomena in physics
Description of how charges interact through the electric field rather than directly
Analogy of electric field lines to the curvature of space-time in gravity
Explanation of the difference between electric and gravitational forces
Discussion on the unification of forces and the search for a repulsive gravitational force
Introduction to Coulomb's law and its application to calculate the force between charges
Description of how electric fields are represented and the direction of field lines
Explanation of the behavior of positive and negative charges in an electric field
Illustration of how multiple charges and their electric fields interact
Derivation of the electric field equation for a point charge
Discussion on the vector nature of the electric field and force
Explanation of how test charges are used to study electric fields
Introduction to the concept of superposition in electric fields
Practical application of calculating the electric field and force on a charge
Discussion on the consistency of physical laws and the self-consistent nature of electric fields
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: