Max and Min and Second Derivative
TLDRIn this informative lecture, the professor introduces the concept of second derivatives, emphasizing their importance in identifying maximum and minimum values in mathematical functions. By using the first derivative to locate potential extremities and the second derivative to determine whether they are maxima or minima, the professor demonstrates the process with various examples, including sine and cosine functions. The discussion also touches on inflection points, where the curvature of a function changes. A practical application is presented through a word problem about optimizing travel time, showcasing the real-world relevance of calculus.
Takeaways
- 📈 The concept of second derivatives is crucial in calculus, especially for determining maximum and minimum values in functions.
- 🔍 The first derivative being zero indicates a potential maximum or minimum, while the second derivative helps in classifying it as either a maximum (negative second derivative) or minimum (positive second derivative).
- 🛣️ An example of applying calculus to real-life scenarios is optimizing travel time by choosing the best entry point to a faster road from a slower one.
- 📊 The lecture introduces the idea of an 'inflection point' where the curvature of a graph changes from concave to convex, signified by the second derivative crossing zero.
- 📚 The connection between distance, speed, and acceleration is highlighted, with the second derivative in the context of motion being equivalent to acceleration.
- 📈 The script provides a detailed walkthrough of how to use calculus to minimize a function, specifically the travel time to a destination by finding the optimal angle of approach.
- 🤔 The importance of correctly identifying the unknown variable in a problem is emphasized, as it is key to setting up the function and applying calculus.
- 📊 The use of Pythagorean theorem is demonstrated to calculate distances in the context of the real-world problem of minimizing travel time.
- 🔢 The process of taking derivatives, applying the chain rule, and solving for the critical points to find maximum and minimum values is thoroughly explained.
- 📈 The script illustrates the power of calculus in solving optimization problems and provides a methodical approach to tackle such tasks.
- 🌐 The video is part of MIT OpenCourseWare, offering free and open access to educational content, supported by the Lord Foundation.
Q & A
What is the primary application of derivatives in calculus?
-The primary application of derivatives in calculus is to locate maximum and minimum values of a function, which can be used to solve optimization problems.
How does the first derivative help in identifying a local maximum or minimum?
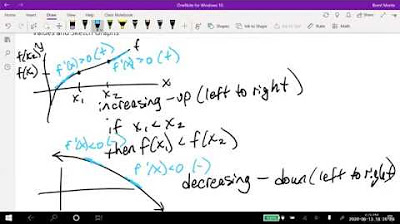
-The first derivative helps in identifying a local maximum or minimum by finding points where the derivative equals zero, indicating a level off or change in the slope of the function.
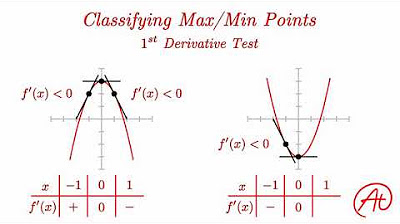
What is the role of the second derivative in determining whether a critical point is a maximum, minimum, or neither?
-The second derivative provides information about the concavity or bending of the graph. A positive second derivative indicates the graph is bending upwards, suggesting a local minimum, while a negative second derivative indicates the graph is bending downwards, suggesting a local maximum.
What is an inflection point and how can it be identified?
-An inflection point is a point on the graph of a function where the concavity changes, meaning the graph switches from bending upwards to downwards or vice versa. It can be identified by finding points where the second derivative is zero and the sign of the second derivative changes.
How does the concept of derivatives relate to physical quantities such as distance, speed, and acceleration?
-In the context of physics, the first derivative of distance with respect to time represents speed, while the second derivative represents acceleration, which is the rate of change of speed.
What is the significance of setting the derivative to zero in calculus problems?
-Setting the derivative to zero is a common technique used to find critical points of a function. These points are where the function's slope is zero and can represent local maxima, local minima, or inflection points.
How does the sign of the second derivative indicate the nature of a critical point?
-A positive second derivative at a critical point indicates a local minimum, where the graph is bending upwards. A negative second derivative indicates a local maximum, where the graph is bending downwards.
What is the process for finding the maximum or minimum value of a function?
-To find the maximum or minimum value of a function, one must first find the critical points by setting the first derivative equal to zero and solving for the variable. Then, analyze the second derivative at these points to determine if they correspond to a maximum, minimum, or neither.
What is an example of a real-world problem that can be modeled and solved using calculus?
-One example is optimizing travel time by determining the most efficient route or angle to take when transitioning from slower city streets to a faster highway, as discussed in the script with the Mass Pike scenario.
How can the Pythagorean theorem be applied in the context of the provided script?
-In the context of the script, the Pythagorean theorem can be applied to calculate the distance on city streets when transitioning from slower to faster roads, as it helps to determine the shortest path in a right-angled triangle formed by the city street distance, the highway distance, and the hypotenuse representing the direct distance to the destination.
Outlines
📚 Introduction to Second Derivatives
The paragraph introduces the concept of second derivatives, emphasizing their importance in identifying maximum and minimum values in mathematical problems. The first derivative's role in locating these points is explained, with the second derivative providing information about the concavity or bending of the graph. The connection between calculus and physics is briefly touched upon, using the example of distance, speed, and acceleration. A simple parabola is used to illustrate the concepts, highlighting how the first derivative is zero at maximum or minimum points, and the second derivative indicates the nature of these points.
📈 Analysis of Sine Function
This paragraph delves into the analysis of the sine function, focusing on its graphical representation and the behavior of its first and second derivatives. The slope of the sine function is discussed, with the derivative of sine being cosine. The second derivative of the sine function is explored, revealing it as negative, which indicates the graph's concavity or bending downwards. The concepts of convex and concave functions are introduced, and the significance of the second derivative in determining the bending of the graph is reiterated.
🔢 Derivative Applications and Inflection Points
The paragraph discusses the application of derivatives in identifying key points on a graph, such as maxima, minima, and inflection points. It explains how the first derivative being zero indicates a potential maximum or minimum, while the second derivative's sign determines the nature of these points. The concept of inflection points is introduced, defined as points where the second derivative is zero, signifying a change in the graph's concavity. Examples are provided to illustrate these concepts, and the importance of understanding the behavior of functions and their derivatives is emphasized.
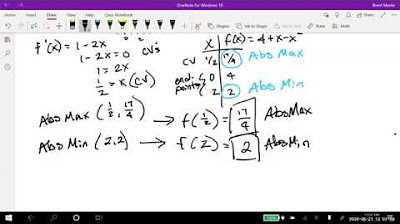
📊 Maxima, Minima, and Inflection Points Identification
This section focuses on the practical application of identifying maxima, minima, and inflection points of a function using its first and second derivatives. The process of setting the first derivative to zero to find potential extrema and then using the second derivative to classify them as maxima, minima, or inflection points is detailed. The discussion includes solving algebraic equations to find the x-values of these points and using the second derivative to confirm their nature. The concept of local versus global extrema is also touched upon.
🚗 Real-world Application: Optimal Route to MIT
The paragraph presents a real-world problem involving the use of calculus to find the most efficient route from the speaker's home to MIT, considering different speeds on city streets and the Mass Pike (highway). The problem is modeled as an optimization problem, where the goal is to minimize travel time. The speaker explains the process of defining the variables, setting up the equation for travel time, and using calculus to find the optimal solution. The importance of understanding the problem and applying calculus concepts to find the minimum is emphasized, and the solution is found using derivative calculations.
🎓 Recap and Conclusion
The final paragraph recaps the main points of the lecture, which focused on the use of derivatives to find maximum and minimum values and identify inflection points. The importance of the second derivative in determining whether a point is a maximum, minimum, or inflection point is highlighted. The lecture's examples, including the sine function and the practical problem of finding the quickest route to MIT, are summarized. The speaker encourages further exploration of these concepts and acknowledges the support of MIT OpenCourseWare and the Lord Foundation.
Mindmap
Keywords
💡Derivatives
💡Maximum and Minimum
💡Second Derivative Test
💡Inflection Point
💡Slope
💡Acceleration
💡Convex and Concave
💡Optimization
💡Critical Points
💡Chain Rule
💡Pythagorean Theorem
Highlights
Second derivatives are introduced as an important concept for understanding maximum and minimum problems.
The first derivative being zero indicates a potential maximum or minimum, while the second derivative determines the nature of the point.
The concept of acceleration is used as a real-world example of the second derivative, relating to the rate of change of speed.
The function y = x^2 is used to illustrate how the first derivative represents the slope and the second derivative represents the bending of the graph.
The sine function is used as an example to demonstrate how the first derivative's sign can change, and how the second derivative can be used to identify inflection points.
An inflection point is defined as a point where the second derivative is zero, indicating a change in the concavity of the function.
The concept of local maximum and minimum is introduced, differentiating them from absolute maximum and minimum.
The process of finding maximum and minimum points on a curve is demonstrated using x^3 - x^2 as an example.
The importance of setting the first derivative to zero to find critical points for maximum and minimum problems is emphasized.
A practical application of calculus is presented through a problem involving optimizing travel time between two points with different speed limits.
The Pythagorean theorem is used to calculate the distance on city streets in the practical problem of optimizing travel time.
The process of taking the derivative of an equation involving a square root and setting it to zero to find an optimal solution is demonstrated.
The concept of the second derivative test is mentioned as a way to confirm whether a critical point is a maximum, minimum, or inflection point.
The importance of considering the end behavior of a function when finding minimum and maximum points is discussed.
The video concludes with a recap of the main points covered, including the use of first and second derivatives in identifying maximum, minimum, and inflection points.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: