Extrema of Functions of Two Variables!

Ian Grigsby

22 Apr 202043:19

EducationalLearning

32 Likes 10 Comments

TLDRThe video script delves into the concept of relative extrema for functions of two variables, a topic crucial for optimizing costs and profits in business. Unlike single-variable functions, finding extrema in this context requires a nuanced approach. The presenter introduces the idea of relative maxima and minima, explaining how they are the largest or smallest values in a function's neighborhood. The focus then shifts to the D-test, or the second partial derivative test, which is akin to the second derivative test for single-variable functions. This method involves finding first and second partial derivatives, solving a system of equations to locate potential extrema, and evaluating a discriminant function, D, to distinguish between maxima, minima, and saddle points. The script illustrates the D-test's application through several examples, emphasizing the importance of perseverance and methodical problem-solving in calculus. The presenter assures viewers that the D-test process will be provided on final exams, encouraging them to practice and internalize the method.

Takeaways

📚 The concept of relative extrema for functions of two variables is important for optimizing multi-variable scenarios like minimizing costs and maximizing profits.
🔍 A relative maximum or minimum occurs where a function's value is the largest or smallest, respectively, compared to all points around it.
📈 To find extrema, first set the first partial derivatives (F_x and F_y) of the function equal to zero, which gives potential extrema points.
⛰️ The issue with only using the first partial derivatives is that it does not distinguish between maxima, minima, and saddle points.
🧐 The second partial derivative test, also known as the D-test, helps differentiate between these types of points by evaluating a specific formula involving second partials.
📝 The D-test formula is D = F_xx * F_yy - (F_xy)^2, where F_xx, F_yy, and F_xy are the second partial derivatives of the function.
🤔 If D > 0 and F_xx > 0, the point is a relative minimum. If D > 0 and F_xx < 0, the point is a relative maximum.
😕 If D < 0, the point is a saddle point, indicating a neither a maximum nor a minimum.
🔢 If D = 0, the test is inconclusive, and another method is needed to determine the nature of the extrema.
📈 The D-test is similar to the second derivative test for functions of one variable, but it's extended for functions with multiple variables.
📚 The process of finding extrema involves finding first and second partial derivatives, solving a system of equations, evaluating the D-test, and interpreting the results.
💪 Despite the complexity of the process, it's essential to persevere and follow the steps to solve multi-variable optimization problems.

Q & A

What are the relative extrema of a function of two variables?
-A function f of X, Y has a relative maximum at a point (X_nought, Y_nought) if it is the largest value out of any points close to it. Similarly, it has a relative minimum at (X_nought, Y_nought) if it's the smallest point compared to all the points around it.
How does the concept of relative extrema relate to the business world?
-In the business world, the concept of relative extrema can be applied to find the最大化利润 (maximize profit) and 最小化成本 (minimize cost). It helps in making strategic decisions to optimize business outcomes.
What are the steps to find the extrema of a function of two variables?
-The steps include: 1) Find the first partial derivatives F_X and F_Y, as well as the second partial derivatives F_XX, F_XY, and F_YY. 2) Solve the system of equations F_X = 0 and F_Y = 0 to find potential extrema points. 3) Evaluate the discriminant D at these points. 4) Interpret the results based on the value of D and the signs of the second partial derivatives.
What is the issue with just setting the first partial derivatives to zero when trying to find extrema of a function of two variables?
-The issue is that setting the first partial derivatives to zero can also yield saddle points, which are not extrema but points where the function neither maximizes nor minimizes. This requires a further test to distinguish between maxima, minima, and saddle points.
What is the D test and how is it used to find relative extrema?
-The D test, also known as the second partial test, is a method to find relative extrema by evaluating a determinant formed from the second partial derivatives at a point. It helps to distinguish between maxima, minima, and saddle points by interpreting the sign of the determinant and the second partial derivatives.
What happens if the determinant D in the D test is positive and F_XX is positive?
-If D is positive and F_XX is also positive, the point is a relative minimum.
What happens if the determinant D in the D test is positive and F_XX is negative?
-If D is positive and F_XX is negative, the point is a relative maximum.
What is the significance of the determinant D being negative in the D test?
-If the determinant D is negative, the point is a saddle point, and there is no need to check the second partial derivatives.
What does it mean if the determinant D in the D test is zero?
-If D is zero, the test provides no information, and another method must be used to determine the nature of the point.
How does the D test relate to the second derivative test for functions of one variable?
-The D test is similar to the second derivative test for functions of one variable, but it involves second partial derivatives instead of just second derivatives. It uses the same concept of concavity to determine whether a point is a maximum, minimum, or saddle point.
Can you provide an example of a function of two variables and demonstrate the process of finding its relative extrema?
-Consider the function f(X, Y) = -3X^2 - 4Y^2 - 6X - 2Y + 9. First, find the first partial derivatives F_X and F_Y, and set them to zero. Solve the system of equations to find potential extrema points. Evaluate the determinant D at these points and interpret the results based on the sign of D and F_XX to determine whether the points are relative maxima, minima, or saddle points.

Outlines

00:00

📚 Introduction to Relative Extrema of Functions with Two Variables

The video begins by introducing the concept of relative extrema for functions of two variables, drawing parallels with the study of derivatives in functions of a single variable. It explains the difference between relative maxima and minima and how they occur at points where the function's value is the largest or smallest, respectively, compared to neighboring points. The video also introduces the concept of absolute extrema and distinguishes it from relative extrema. It then suggests using the first derivative test as a starting point for finding extrema by setting the partial derivatives equal to zero, which leads to critical points.

05:01

🔍 Critical Points and the Issue of Saddle Points

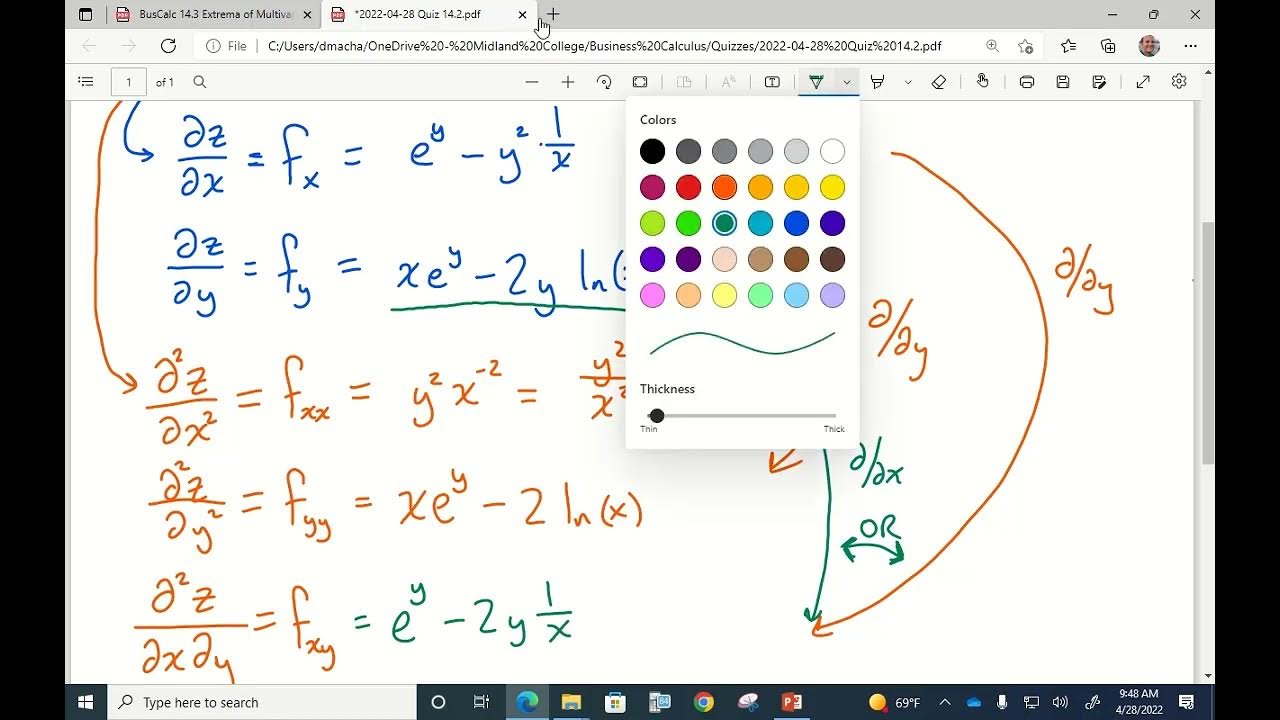
The video moves on to discuss the limitations of simply setting the first partial derivatives to zero, highlighting the issue of saddle points. These are points where both partial derivatives are zero but do not represent a maximum or minimum. The video then introduces the second partial derivative test, also known as the D-test, as a method to differentiate between maxima, minima, and saddle points. It outlines a four-step process involving finding the first and second partial derivatives, solving a system of equations for potential extrema, evaluating a discriminant D at the critical points, and interpreting the results to determine the nature of the extrema.

10:04

🔢 Application of the D-test with an Example

The video provides a step-by-step application of the D-test using an example function. It demonstrates how to find the first and second partial derivatives, solve the system of equations to find critical points, evaluate the discriminant D at these points, and interpret the results to find the relative extrema. The example clarifies how to identify whether a point is a maximum, minimum, or saddle point using the D-test.

15:07

🔗 Solving Systems of Equations and Evaluating D

This part of the video continues the application of the D-test with another example, emphasizing the process of solving systems of equations to find potential extrema. It also shows how to evaluate the function D at these points, which is crucial for determining the nature of the extrema. The video simplifies the second partial derivatives and evaluates them at the critical points to find the value of D, which is then used to interpret the results in the next step.

20:08

📉 Interpreting Results and Identifying Relative Extrema

The video explains how to interpret the results from the D-test to identify relative maxima, minima, or saddle points. It discusses the implications of D being positive or negative and how the sign of the second partial derivatives F_xx and F_yy influence the final interpretation. The video concludes with an example that walks through the entire process, from finding partial derivatives to interpreting the D-test results.

25:09

🧮 Chain Rule and Product Rule in Partial Derivatives

The video delves into the application of the chain rule and product rule when finding second partial derivatives, especially in functions involving powers and products. It emphasizes the importance of a meticulous approach to ensure accurate results. The presenter simplifies the expressions for second partial derivatives and prepares them for substitution into the D-test formula.

30:10

🔍 Simplifying Second Partial Derivatives

This section focuses on simplifying the expressions for second partial derivatives, which can be quite complex. The video demonstrates algebraic manipulation and simplification techniques to make the derivatives easier to handle. It also shows how to factor out common terms and powers to simplify the expressions before substituting them into the D-test.

35:13

🧷 Solving Fractional Equations and Finding Solutions

The video addresses the process of solving fractional equations that arise from setting the first partial derivatives to zero. It simplifies these equations to find the solutions, which represent the critical points where the nature of the extrema will be determined. The solutions are then used to evaluate the D-test and interpret the results.

40:16

📐 Evaluating D at Critical Points

The presenter evaluates the D function at the critical points found from the previous step. This involves substituting the critical point values into the second partial derivatives. The video shows the calculations for F_xx, F_yy, and F_xy at the critical points, emphasizing the importance of careful computation.

📈 Interpreting D Function and Finalizing Extrema

The final part of the video interprets the value of the D function at the critical points. It explains how the sign of D, in conjunction with the signs of the second partial derivatives, determines whether the point is a relative maximum, minimum, or saddle point. The video concludes by summarizing the process and encouraging viewers to practice the method on homework problems.

Mindmap

Keywords

💡Extrema

Extrema refers to the highest (maximum) or lowest (minimum) values of a function. In the context of the video, it is about finding where these points occur for functions of two variables, which is crucial in various applications such as minimizing costs or maximizing profits. The video discusses how to identify relative maxima and minima, which are the highest or lowest points in a function's neighborhood.

💡Derivatives

Derivatives are a mathematical concept that describes the rate at which a function changes. In the video, first and second derivatives are used to find critical points and to determine the nature of extrema. The first derivative test is a method for locating points where extrema might occur, while the second derivative test helps in classifying these points as maxima, minima, or saddle points.

💡Saddle Points

Saddle points are points on a surface where the first partial derivatives are zero but do not correspond to a local maximum or minimum. They are a type of critical point that can be misleading if only the first derivative test is used. The video explains that saddle points are important to distinguish from true maxima and minima, especially when using the second partial derivative test.

💡Second Partials Test

The second partials test, also known as the D-test, is a method used to determine whether a critical point is a relative maximum, minimum, or a saddle point. It involves evaluating a specific determinant formed from the second partial derivatives of the function. The video provides a step-by-step guide on how to apply this test to functions of two variables.

💡Continuous Second Partial Derivatives

Continuous second partial derivatives are a requirement for using the second partials test. It means that the second order partial derivatives of the function exist and are continuous in the region of interest. The video emphasizes that this condition must be met before applying the second partials test to find relative extrema.

💡Relative Maximum/Minimum

A relative maximum or minimum is a point on the graph of a function where the function's value is higher or lower, respectively, than the values of the function at all nearby points. The video explains how to find these points using calculus, which is essential for optimization problems in fields like business and economics.

💡Absolute Maximum/Minimum

An absolute maximum or minimum is a point on the graph of a function where the function's value is the highest or lowest, respectively, over the entire domain of the function. The video distinguishes between relative and absolute extrema, noting that the focus is on relative extrema, which are local rather than global.

💡First Order Partial Derivatives

First order partial derivatives of a function of multiple variables represent the rate of change of the function with respect to each variable, holding the other variables constant. In the video, setting these derivatives equal to zero is the first step in finding critical points, which are potential locations for relative extrema.

💡Second Order Partial Derivatives

Second order partial derivatives are the derivatives of the first order partial derivatives and provide information about the curvature of the function. In the video, these derivatives are used in the second partials test to determine the nature of critical points found by setting the first order partial derivatives to zero.

💡Discriminant of Second Partials (D)

The discriminant of second partials, often referred to as 'D', is a determinant used in the second partials test to classify critical points. It is calculated using the second partial derivatives of the function. The sign of D, along with the signs of certain second partial derivatives, helps determine whether a critical point is a relative maximum, minimum, or saddle point.

💡Chain Rule

The chain rule is a fundamental theorem in calculus used for finding the derivative of composite functions. In the video, it is mentioned in the context of finding partial derivatives of functions involving powers or other complex expressions. The chain rule is essential for correctly calculating the second partial derivatives needed for the second partials test.

Highlights

Introduction to the concept of relative extrema for functions of two variables, which is essential for applications like minimizing cost and maximizing profit.

Definition of a relative maximum and minimum for a function f(x, y) in terms of neighboring points.

Graphical representation of relative maxima and minima using a 3D graph, illustrating peaks and valleys.

Differentiation between relative extrema and absolute extrema in terms of global maximum and minimum points.

Methodology to find extrema by setting the first partial derivatives equal to zero, leading to critical points.

Challenge of identifying saddle points when both first partial derivatives are zero, which do not represent maxima or minima.

Introduction of the second partials test, also known as the D-test, to distinguish between maxima, minima, and saddle points.

Process to find relative extrema involving finding first and second partial derivatives, solving a system of equations, and evaluating a discriminant function D.

Interpretation of results from the D-test to determine the nature of the critical points as maxima, minima, or saddle points.

Example of applying the D-test to the function f(x, y) = -3x^2 - 4y^2 - 6x - 2y + 9 to find relative extrema.

Demonstration of solving a system of equations derived from setting first partial derivatives to zero to find potential extrema.

Evaluation of the D-test for a more complex function involving products and chain rules in partial derivatives.

Simplification techniques for second partial derivatives to make the application of the D-test more manageable.

Another example using the D-test for the function f(x, y) = -5x^2 + 4xy - y^2 + 16x + 10y, showcasing the process step by step.

Final example with a function involving a power of a sum, emphasizing the use of the chain rule and product rule in finding partial derivatives.

Emphasis on perseverance and sticking to the process when dealing with complex derivatives, as demonstrated in the final example.

Summary and recap of the process for finding relative extrema of functions of two variables, highlighting the importance and practical applications.

Transcripts

Browse More Related Video

Warm up to the second partial derivative test

BusCalc 14.3 Extrema of Multivariable Functions

Second Derivative Test Multivariable (Calculus 3)

Use the Second Derivative Test to Find Any Extrema and Saddle Points: f(x,y) = -4x^2 + 8y^2 - 3

Calculus AB Homework 4.4: Relative Extrema

Second partial derivative test intuition

Related Tags

Mathematics Derivatives Optimization Business Maxima Minima Critical Points Second Derivative Test D Test Function Analysis