GCSE Physics - Acceleration #52

Cognito
1 Dec 201905:15
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the concept of acceleration, defined as the rate of change in velocity. It introduces two key equations related to acceleration, emphasizing the difference between instantaneous and average acceleration. The video uses a car's acceleration example to illustrate the calculation and highlights the vector nature of acceleration. It also addresses the second equation involving distance, applicable when time is unknown, using a ball drop scenario to demonstrate its application. The content is engaging, informative, and encourages viewers to explore the principles of motion and acceleration further.

Takeaways
  • πŸ“ˆ Acceleration is the rate of change in velocity, indicating how quickly an object speeds up or slows down.
  • πŸ“ The formula for acceleration is Ξ”v = u - v, where v is the final velocity, u is the initial velocity, and Ξ”v represents the change in velocity.
  • πŸš— An example of calculating acceleration is finding the change in velocity (35 m/s - 15 m/s) over a time period (5 seconds), resulting in 4 m/sΒ².
  • 🎯 Acceleration is a vector quantity, meaning it has both direction and magnitude, and can be negative to represent deceleration.
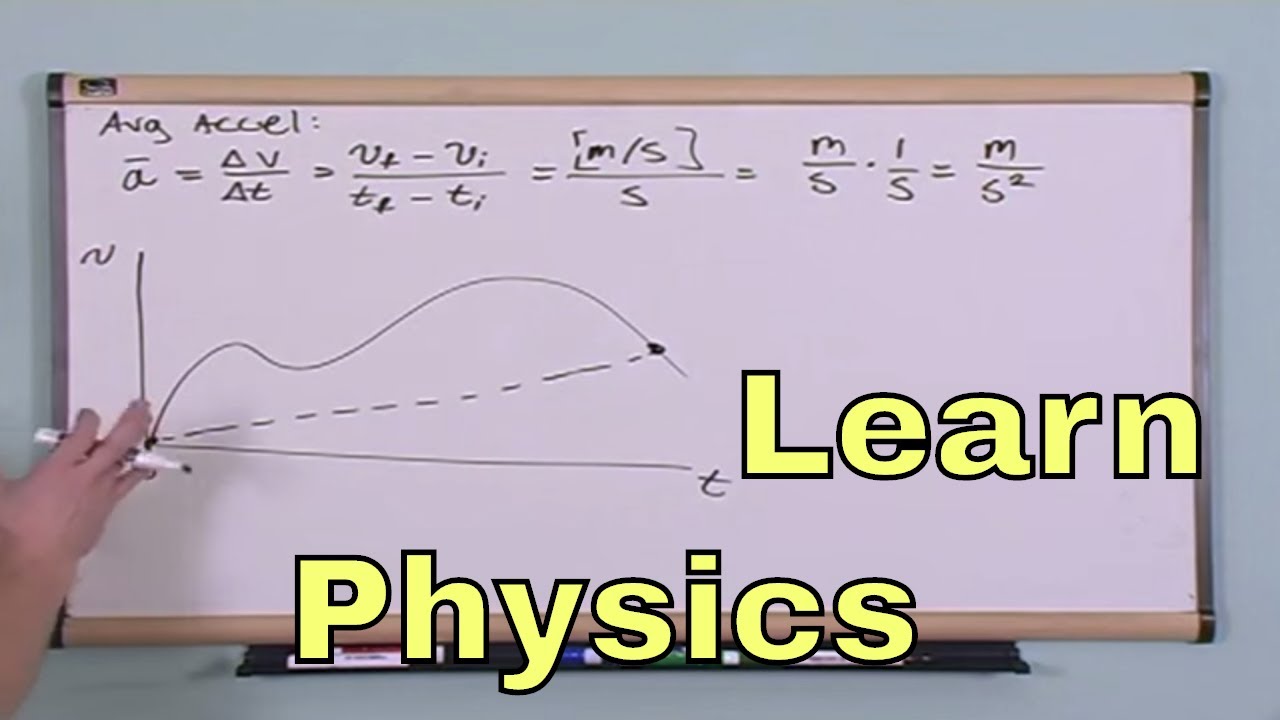
  • 🌐 Average acceleration is calculated over a period of time and may not represent constant acceleration throughout the interval.
  • πŸ›€οΈ There are two main acceleration equations; one involving time and the other involving distance, to be used based on the given information.
  • πŸ† When an object starts from stationary, its initial velocity (u) is zero.
  • πŸ”„ To find distance (s), rearrange the distance formula and plug in known values (vΒ² - uΒ²) / 2a.
  • 🏐 An example calculation for distance shows that a ball dropped from rest with a final velocity of 7 m/s would have been 2.5 meters above the ground.
  • πŸ“Š Understanding acceleration and its related equations is crucial for solving problems involving changes in velocity and distance.
Q & A

  • What is acceleration?

    -Acceleration is the rate of change in velocity, which means how quickly something speeds up or slows down.

  • How is acceleration measured?

    -Acceleration is measured in meters per second squared (m/s^2).

  • What do the two important equations for acceleration represent?

    -The two important equations represent the relationship between acceleration, change in velocity, time, and distance.

  • What does the delta sign (βˆ†) signify in the context of these equations?

    -The delta sign (βˆ†) signifies change, for example, βˆ†v means change in velocity.

  • How can you express the change in velocity?

    -You can express the change in velocity as βˆ†v, v - u, where v is the final velocity and u is the initial velocity.

  • How do you calculate the acceleration of a car that accelerates from 15 to 35 meters per second over 5 seconds?

    -You calculate the car's acceleration by finding the change in velocity (35 m/s - 15 m/s = 20 m/s) and dividing it by the time (5 seconds), resulting in an acceleration of 4 m/s^2.

  • What does it mean for acceleration to be a vector quantity?

    -Being a vector quantity means that acceleration has both direction and magnitude, and it can be negative, indicating deceleration or slowing down.

  • What is average acceleration, and why might it differ from constant acceleration?

    -Average acceleration is the overall change in velocity divided by the total time taken. It differs from constant acceleration because the rate of change of velocity may not be uniform throughout the time interval, such as accelerating more in the initial seconds and less in the following seconds.

  • How do you use the second acceleration equation when given the distance and the conditions of the scenario?

    -You use the second acceleration equation by rearranging it to solve for distance (s), which involves dividing (v^2 - u^2) by 2a, and then plugging in the known values of final velocity, initial velocity, and acceleration due to gravity.

  • In the example of the ball dropped from an unknown height, how do you determine the height?

    -You determine the height by assuming the ball starts from rest (initial velocity, u = 0 m/s), knowing the final velocity (v = 7 m/s), and using the acceleration due to gravity (9.8 m/s^2) in the rearranged second acceleration equation.

  • What is the significance of knowing whether an object starts from stationary in these calculations?

    -Knowing whether an object starts from stationary is significant because it establishes the initial velocity (u = 0 m/s), which simplifies the calculations and helps in applying the correct formulas.

  • How does air resistance affect the calculations of acceleration?

    -Air resistance affects the calculations because it introduces a drag force that opposes the motion, causing the actual acceleration to be different from the theoretical acceleration due to gravity alone, which is only considered when ignoring air resistance.

Outlines
00:00
πŸš€ Understanding Acceleration and its Calculation

This paragraph introduces the concept of acceleration, defined as the rate of change in velocity, or how quickly an object speeds up or slows down. It emphasizes the importance of two key equations for comprehending acceleration. The first equation relates acceleration (in meters per second squared) to the change in velocity (delta v, which can also be expressed as v - u, with v being the final velocity and u the initial velocity) over time. The example of a car accelerating from 15 to 35 meters per second in 5 seconds is used to illustrate the calculation of acceleration. The paragraph also explains that acceleration is a vector quantity with both magnitude and direction, and can be negative, indicating deceleration. It further discusses the concept of average acceleration and contrasts it with uniform or constant acceleration. Lastly, it introduces a second acceleration equation involving distance, which is useful when the unit of distance is provided.

05:02
🌟 Engaging with the Content and Future Videos

The second paragraph serves as a call to action for viewers, encouraging them to like and subscribe for more content. It implies that there will be future videos on related topics, and seeks viewer engagement to continue the learning experience.

Mindmap
Keywords
πŸ’‘Acceleration
Acceleration is the rate at which an object changes its velocity, meaning how quickly it speeds up or slows down. In the context of the video, it is a central concept used to describe the motion of objects. It is measured in meters per second squared (m/s^2) and is a vector quantity, indicating it has both magnitude and direction. An example from the script is the calculation of a car's acceleration as it goes from 15 to 35 meters per second over a period of 5 seconds, resulting in an acceleration of 4 m/s^2.
πŸ’‘Velocity
Velocity is a vector quantity that describes the speed and direction of an object's motion. In the video, it is fundamental to understanding acceleration since acceleration is the change in velocity over time. The script uses the difference between final velocity (v) and initial velocity (u) to illustrate how velocity changes, which is essential for calculating acceleration.
πŸ’‘Delta Sign (Ξ”)
The delta sign (Ξ”) is used in mathematics and physics to denote change. In the video, it is used to represent the change in velocity (Ξ”v), which is crucial for determining acceleration. The concept is introduced to help viewers understand how to calculate the difference between the final and initial velocities of an object.
πŸ’‘Time
Time is a fundamental factor in the calculation of acceleration, as it is the interval over which the change in velocity occurs. The video emphasizes the importance of time in understanding how acceleration is computed, specifically as the period over which an object speeds up or slows down.
πŸ’‘Final Velocity (v)
Final velocity (v) refers to the speed of an object at the end of a specified time interval or after a certain event. In the video, the final velocity is a critical value needed to calculate the change in velocity and, subsequently, the acceleration of an object. It is used in the context of understanding motion and how it changes over time.
πŸ’‘Initial Velocity (u)
Initial velocity (u) is the speed of an object at the beginning of a specified time interval or event. The video highlights that initial velocity is essential for determining the change in velocity (Ξ”v) and, therefore, the acceleration of an object. It sets the starting point for velocity calculations.
πŸ’‘Average Acceleration
Average acceleration is the overall change in velocity of an object over a specific time period. The video explains that the calculated acceleration might be an average value, especially if the acceleration is not constant. This concept is important for understanding the general motion of an object when the acceleration may vary over time.
πŸ’‘Uniform Acceleration
Uniform acceleration, also known as constant acceleration, occurs when an object's acceleration remains the same over time. The video introduces this concept to contrast with variable acceleration, where the rate of change of velocity is not constant. Understanding uniform acceleration is crucial for analyzing situations where an object's motion is consistently sped up or slowed down at a steady rate.
πŸ’‘Distance
Distance is the total length of the path traveled by an object. In the context of the video, distance is included in the second acceleration equation, which relates acceleration, initial velocity, final velocity, and distance. This concept is vital for solving problems where the displacement or path length of an object is relevant.
πŸ’‘Gravity
Gravity is the force that attracts two bodies towards each other, and in the context of the video, it is the force that causes objects to accelerate downwards when dropped. The acceleration due to gravity is approximately 9.8 m/s^2 near the Earth's surface, which is a standard value used in calculations involving free-fall motion.
πŸ’‘Stationary
In physics, an object is considered stationary when it has zero velocity, meaning it is not moving. The video emphasizes that the initial velocity (u) of an object dropped from rest or thrown upwards is zero. This is a critical assumption that simplifies the calculation of motion and acceleration in various scenarios.
Highlights

Acceleration is defined as the rate of change in velocity, which can be described as how quickly an object speeds up or slows down.

The primary equation for acceleration is given as acceleration equals the change in velocity divided by time, with acceleration measured in meters per second squared.

The delta sign (βˆ†) represents change, and in the context of velocity, βˆ†v means the change in velocity, which can also be expressed as final velocity (v) minus initial velocity (u).

An example is provided where a car accelerates from 15 to 35 meters per second in 5 seconds, with the initial velocity being 15 m/s and the final velocity being 35 m/s.

The car's acceleration is calculated as 4 meters per second squared by finding the change in velocity (20 m/s) and dividing it by the time interval (5 seconds).

Acceleration is a vector quantity, similar to velocity, which means it has both direction and magnitude, and can be negative, indicating a decrease in speed or deceleration.

The example given for the car's acceleration represents the average acceleration over the 5-second period, acknowledging that in reality, acceleration may not be constant.

Uniform or constant acceleration is used to describe a scenario where an object accelerates at the same rate over a period of time.

The second acceleration equation includes distance, which is used when the unit of distance is provided instead of time.

When an object starts from stationary, its initial velocity (u) is zero, simplifying the equations for such scenarios.

A practical application of the second equation is demonstrated by calculating the height from which a ball is dropped, given its final velocity and ignoring air resistance.

The ball's initial velocity is assumed to be zero since it was dropped, and it accelerates downward at 9.8 meters per second squared due to gravity.

To find the distance the ball was dropped, the second equation is rearranged and values are plugged in, resulting in the calculation of the height as 2.5 meters.

The video provides a comprehensive overview of the concept of acceleration, its equations, and practical applications, making it a valuable resource for understanding this fundamental principle of physics.

The video's content is engaging and informative, offering clear explanations and examples that effectively clarify the concept of acceleration and its relevance in real-world scenarios.

The video concludes with a call to action for viewers to like and subscribe if they found the content useful, promoting further engagement and learning.

Transcripts

Browse More Related Video

8.01x - Lect 2 - 1D Kinematics - Speed, Velocity, Acceleration

College Physics 1: Lecture 8 - Acceleration

Average velocity for constant acceleration | One-dimensional motion | Physics | Khan Academy

01 - Velocity And Acceleration In 1-D (Physics Tutor)

Creating And Using Kinematic Equations Chart - Kinematics - Physics

Calculus - Position Average Velocity Acceleration - Distance & Displacement - Derivatives & Limits

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsAcceleration CalculationVelocity ChangeMeters per SecondUniform MotionGravity ForceMotion AnalysisEducational ContentScience EducationMechanics Principles