1. The Geometry of Linear Equations
TLDRIn the first lecture of MIT's course 18.06 on linear algebra, Professor Gilbert Strang introduces the fundamental problem of solving a system of linear equations. He explains the concepts of row and column pictures, and how they relate to the matrix form of linear equations. Using examples with two and three variables, he illustrates the geometric interpretation of linear algebra and the importance of linear combinations in finding solutions. The lecture sets the stage for deeper exploration of matrix multiplication, invertible matrices, and the conditions under which every right-hand side can be achieved.
Takeaways
- 📚 The lecture is the first in MIT's course 18.06 on linear algebra, taught by Gilbert Strang, with the textbook 'Introduction to Linear Algebra' as the main resource.
- 💻 The course web page (web.mit.edu/18.06) provides exercises, past Matlab codes, and the syllabus for the course.
- 🎯 The fundamental problem of linear algebra is solving a system of linear equations, which can be approached with a specific number of equations and unknowns.
- 📈 The 'Row picture' represents each equation as a line in a two-dimensional plane, where the intersection of lines indicates a solution.
- 🌟 The 'Column picture' is a key concept where the columns of the coefficient matrix are combined linearly to match the right-hand side vector.
- 🔍 The process of finding the right linear combination of columns to achieve the desired right-hand side vector is fundamental to understanding linear algebra operations.
- 📊 In a two-by-two system, the solution is found at the intersection of the lines represented by the equations, if they intersect at a single point.
- 🔢 The matrix form of a linear equation system is Ax = b, where A is the coefficient matrix, x is the vector of unknowns, and b is the right-hand side vector.
- 🤔 The question of whether every right-hand side b can be achieved through a linear combination of the columns of A is crucial for understanding the solvability of the system.
- 🚫 A system may not have a solution if the columns of A are linearly dependent, meaning they lie in the same plane, and thus cannot produce all possible right-hand sides in the space.
- 📝 The next lecture will cover elimination methods, a systematic approach to finding solutions to linear systems and determining when a solution exists or not.
Q & A
What is the fundamental problem of linear algebra discussed in the lecture?
-The fundamental problem of linear algebra discussed in the lecture is to solve a system of linear equations.
What is the text for the course 18.06 at MIT?
-The text for the course 18.06 at MIT is 'Introduction to Linear Algebra'.
What is the role of the course web page for 18.06?
-The course web page for 18.06 provides a variety of resources including exercises from the past, MatLab codes, and the syllabus for the course.
How is the coefficient matrix represented in the context of linear equations?
-The coefficient matrix is represented as a rectangular array of numbers, with the numbers coming from the coefficients of the variables in the equations.
What does the 'Row picture' in linear algebra represent?
-The 'Row picture' in linear algebra represents the graphical representation of the solutions to each equation in a system of linear equations, where each row corresponds to a line in the xy-plane.
What is the significance of the 'column picture' in understanding linear equations?
-The 'column picture' is significant because it represents the concept of linear combinations of the columns of the coefficient matrix, which is fundamental to solving the system of linear equations.
How does the lecture demonstrate the solution to a system of two linear equations with two unknowns?
-The lecture demonstrates the solution by plotting the lines represented by each equation on the xy-plane and finding the point where they intersect, which is the solution to the system.
What is the matrix form of a system of linear equations?
-The matrix form of a system of linear equations is Ax = b, where A is the coefficient matrix, x is the vector of unknowns, and b is the vector of constants from the right-hand side of the equations.
What does the lecture imply about the relationship between the columns of a matrix and the solutions to the system of equations?
-The lecture implies that the columns of a matrix, when combined through linear combinations, can represent the solutions to the system of equations. If the columns are linearly independent and span the space, then every right-hand side b can be reached.
How does the lecture introduce the concept of matrix multiplication by vectors?
-The lecture introduces the concept of matrix multiplication by vectors through the process of finding a solution to a system of linear equations, emphasizing the idea of combining the columns of the matrix in the right amounts to produce the vector on the right-hand side.
What is the significance of the point where three planes meet in a three-dimensional system of linear equations?
-The point where three planes meet in a three-dimensional system of linear equations is the solution to the system, provided that the planes are not parallel and do not lie along the same line.
What happens when the columns of a matrix lie in the same plane?
-When the columns of a matrix lie in the same plane, the linear combinations of these columns will also lie in that plane, which means that not all right-hand sides b can be reached, and the system will not have a solution for every b.
Outlines
📘 Introduction to Linear Algebra and Course Overview
The paragraph introduces the first lecture of MIT's course 18.06, Linear Algebra, taught by Gilbert Strang. It highlights the textbook 'Introduction to Linear Algebra' as the course material and mentions the course web page for additional resources like exercises, MatLab codes, and the syllabus. The lecture's primary focus is on solving a system of linear equations and begins with an example of two equations with two unknowns, using the Row and Column pictures to visualize the problem. The introduction also touches on the matrix form of representing these equations, where the matrix A represents the coefficients, and the vector b represents the right-hand side values.
📊 Visualizing Linear Equations: Row and Column Pictures
This paragraph delves deeper into the visualization of linear equations using the Row and Column pictures. It explains how lines representing individual equations intersect at points and how these points can be plotted on an xy-plane. The Row picture involves plotting points that satisfy each equation and finding their intersection, which represents the solution. The Column picture, on the other hand, focuses on combining the columns of the matrix (representing the coefficients) in the right proportions to match the right-hand side vector. The paragraph emphasizes the importance of understanding these visualizations for grasping the fundamental operations in linear algebra.
🔢 Linear Combinations and the Essence of Linear Algebra
The paragraph discusses the concept of linear combinations, which is central to understanding linear algebra. It explains how a linear combination of the columns of a matrix can produce a desired vector on the right-hand side. The example given illustrates how to find the correct combination by multiplying and adding the column vectors to achieve the target vector. The paragraph also introduces the idea that the set of all possible linear combinations of the matrix's columns can fill the entire space, which is a crucial concept in determining whether a system of equations has a solution for every possible right-hand side vector.
📈 Extending Concepts to Three-Dimensional Systems
This paragraph extends the previously discussed concepts to three-dimensional systems, using a three-by-three matrix and a three-dimensional right-hand side vector. It explains how each row of the matrix represents a plane in three-dimensional space, and the solution to the system is the point where these planes intersect. The paragraph also touches on the challenges of visualizing higher-dimensional spaces and emphasizes the importance of the column picture in understanding how to combine the columns to achieve the right-hand side vector.
🤔 Exploring the Possibilities of Solving Systems for All Right-Hand Sides
The paragraph explores the question of whether a given system of linear equations can be solved for every possible right-hand side vector. It introduces the idea of a non-singular or invertible matrix, which allows for solutions for every right-hand side. The scenario where columns of the matrix lie in the same plane, leading to a singular matrix, is also discussed, explaining that this would limit the right-hand side vectors for which solutions exist. The paragraph concludes with a brief consideration of higher-dimensional systems and the concept of linear combinations filling the entire space or being limited to a lower-dimensional subspace.
🔄 Matrix Multiplication and Its Interpretation
This paragraph focuses on the process of matrix multiplication by a vector, explaining it in the context of linear combinations of the matrix's columns. Two methods of matrix-vector multiplication are discussed: column-wise and row-wise. The column-wise approach views the multiplication as creating a linear combination of the columns, while the row-wise method involves taking the dot product of each row with the vector. The paragraph emphasizes the column-wise interpretation, encouraging students to think of matrix multiplication as a combination of columns, which will be useful in understanding more complex concepts later in the course.
🎓 Final Thoughts and Looking Forward to Elimination Techniques
In the concluding paragraph, the lecturer summarizes the concepts covered in the lecture and sets the stage for future topics. The importance of understanding the matrix form of linear equations and the visualization of these equations through row and column pictures is reiterated. The lecture ends with a teaser for the next session, which will cover elimination techniques—a systematic method for solving systems of linear equations and determining the existence of solutions. The lecturer thanks the audience and encourages them to look forward to learning more about linear algebra in the upcoming lectures.
Mindmap
Keywords
💡Linear Algebra
💡Systems of Linear Equations
💡Matrix
💡Vector
💡Row Picture
💡Column Picture
💡Linear Combination
💡Solving Equations
💡Gilbert Strang
💡MIT Course 18.06
Highlights
Introduction to MIT's course 18.06, linear algebra, by Gilbert Strang.
The textbook for the course is 'Introduction to Linear Algebra'.
Course materials, including exercises and MATLAB codes, can be found on the course web page at web.mit.edu/18.06.
The fundamental problem of linear algebra is solving a system of linear equations.
The first lecture focuses on a case with n equations and n unknowns, which is the 'normal, nice case'.
The 'Row picture' describes each equation individually, showing how lines meet in two-dimensional space.
The 'Column picture' involves looking at the rows and columns of a matrix, introducing the matrix form of the problem.
The algebraic approach involves using a matrix A and a vector of unknowns, with the goal of solving the equation Ax = b.
An example of a two-equation, two-unknown system is given, with the equations 2x - y = 0 and -x + 2y = 3.
The coefficient matrix for the example is a 2x2 matrix with elements [2, -1; -1, 2].
The solution to the system of equations is found to be the point (1, 2), which lies on both lines.
The concept of linear combinations is introduced as the fundamental operation in linear algebra.
The column picture is used to visualize the linear combination of matrix columns to achieve the right-hand side vector.
The lecture discusses the idea of solving for every possible right-hand side b, which depends on the columns of the matrix.
A matrix where the columns are not independent, such as when one column is a sum of others, leads to a singular case where not all right-hand sides can be achieved.
The transition from two dimensions to higher dimensions is discussed, with a focus on the potential of nine-dimensional space.
Matrix multiplication is explained as a linear combination of columns, using either a row-by-row or column-by-column approach.
The importance of matrix multiplication as A times x, where A is the matrix of coefficients and x is the vector of unknowns, is emphasized.
Transcripts
Browse More Related Video
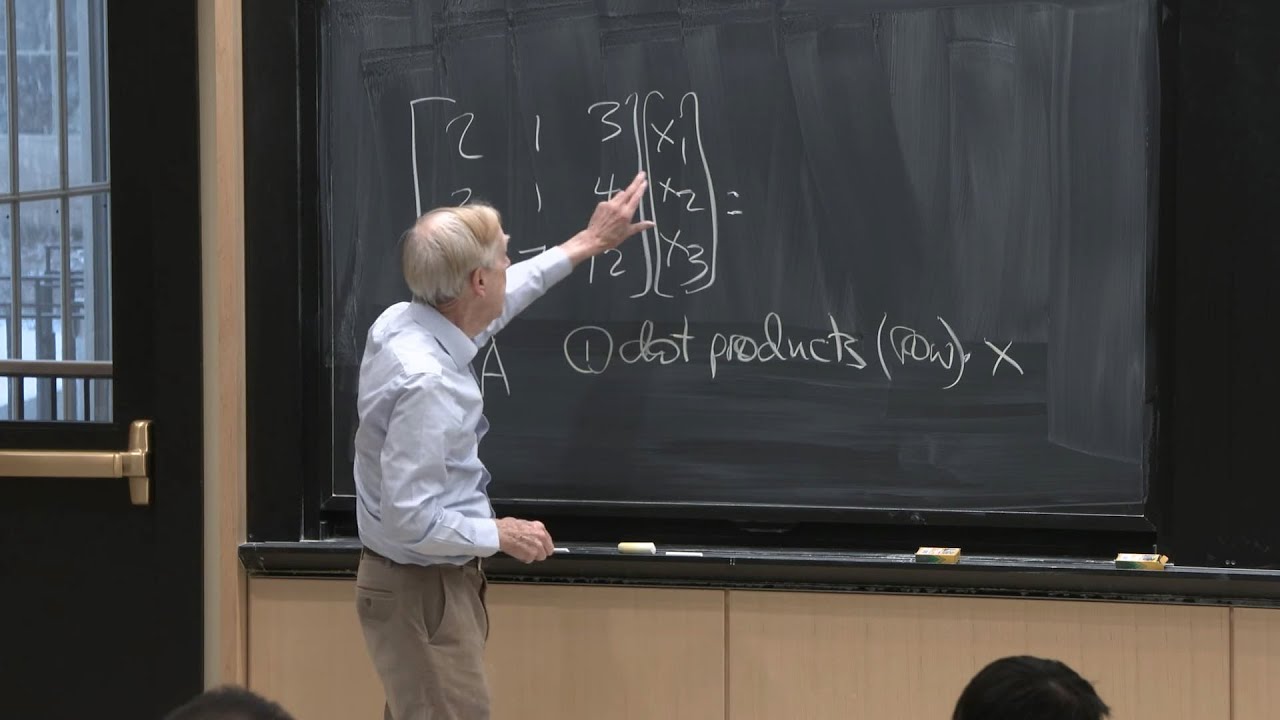
Lecture 1: The Column Space of A Contains All Vectors Ax

Matrices to solve a system of equations | Matrices | Precalculus | Khan Academy

The Big Picture of Linear Algebra

Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra

Algebra 55 - Gauss-Jordan Elimination

Types of Matrices with Examples
5.0 / 5 (0 votes)
Thanks for rating: