The Big Picture of Linear Algebra
TLDRIn this video script, Professor Gilbert Strang delves into the concept of subspaces within the realm of linear algebra, focusing on four key subspaces: the row space, null space, column space, and the null space of the transposed matrix (A^T). He explains that the row space is a plane formed by the linear combinations of two given vectors, while the null space is a line perpendicular to the row space, representing all vectors that result in the zero vector when multiplied by the matrix A. The column space, in this example, encompasses the entire two-dimensional space since the matrix's columns span it. Lastly, the null space of A^T is shown to be trivial, containing only the zero vector for a 2x3 matrix. Strang emphasizes the relationship between the dimensions of these subspaces, highlighting the rank of the matrix as a pivotal quantity, equal to the dimensions of the row and column spaces. This insight leads to the conclusion that the sum of the dimensions of the null space and the column space equals the number of columns (N), and similarly for the row space and the null space of A^T, which equals the number of rows (M). The script provides a geometric and algebraic understanding of subspaces, offering a clear picture of their interrelations and their roles in linear algebra.
Takeaways
- 📐 **Linear Algebra Overview**: The video discusses the big picture of linear algebra, focusing on subspaces rather than a comprehensive course.
- 📚 **Course Reference**: A full course on linear algebra is available on OpenCourseWare 1806, while this session concentrates on differential equations in the context of linear algebra.
- 🔍 **Subspaces in Linear Algebra**: Four fundamental subspaces are introduced: column space, null space, row space, and the null space of the transpose of the matrix (A transpose).
- 📏 **Row Space Definition**: The row space is a plane formed by all linear combinations of the matrix's row vectors.
- ➡️ **Null Space Explanation**: The null space consists of all vectors that, when multiplied by the matrix A, result in the zero vector; it's a line in this example, perpendicular to the row space.
- 🔄 **Independence and Combinations**: The key idea is that linear combinations of vectors fill the space, and the independence of vectors defines the dimension of the space they span.
- 📈 **Column Space Characteristics**: The column space of a matrix is the set of all linear combinations of its column vectors, which, in this example, constitutes the entire two-dimensional space.
- 🔄 **Transposing the Matrix**: By transposing matrix A, the row space of the original matrix becomes the column space of the transposed matrix, A transpose.
- 🔢 **Null Space of A Transpose**: For the given 2x3 matrix example, the null space of A transpose is just the zero vector, indicating a very small or trivial null space.
- 🧮 **Subspace Dimensions**: The dimensions of the four subspaces are interrelated, with the row space and column space sharing the same dimension (the rank of the matrix), and the null spaces spanning the remaining dimensions of their respective ambient spaces.
- 🔑 **Rank of a Matrix**: The rank of matrix A, denoted as R, is a pivotal number representing the dimension of the row space (and column space) and is key to understanding the matrix's subspaces.
Q & A
What is the main focus of the video set that Professor Strang is discussing?
-The main focus of the video set is on differential equations within the context of linear algebra, rather than a full course on linear algebra.
What are the four subspaces mentioned by Professor Strang?
-The four subspaces mentioned are the column space, the null space, the row space, and the null space of the transpose of the matrix (A transpose).
How does the row space of a matrix relate to the vectors within it?
-The row space consists of all linear combinations of the rows of the matrix, which together fill a plane in three-dimensional space.
What is the significance of the null space in relation to the matrix?
-The null space is the set of all vectors that, when multiplied by the matrix, result in the zero vector. It is a one-dimensional subspace that is perpendicular to the row space.
How does the column space of a matrix relate to the dimensions of the space?
-The column space of a matrix fills out a space whose dimension is determined by the number of independent columns, which is the same as the number of independent rows, also known as the rank of the matrix.
What is the rank of a matrix and why is it important?
-The rank of a matrix is the number of independent rows (or columns) in the matrix. It is important because it equals the dimension of both the row space and the column space.
How does the null space of the transpose of a matrix (A transpose) differ from the null space of the original matrix?
-The null space of A transpose consists of all vectors w that satisfy the equation A transpose w equals the zero vector. In the example given, the null space of A transpose is just the zero subspace, containing only the zero vector.
What is the relationship between the dimensions of the four subspaces of a matrix?
-The dimensions of the four subspaces are related such that the sum of the dimensions of the row space and the null space equals the number of rows (N) of the matrix, and the sum of the dimensions of the column space and the null space of A transpose equals the number of columns (M) of the matrix.
How does the concept of linear combinations play a role in defining the row space?
-Linear combinations of the rows of a matrix are used to define the row space, as they represent all possible combinations that can be formed from the row vectors, effectively filling a plane in the space.
What does it mean for two subspaces to be perpendicular?
-Two subspaces are perpendicular if every vector in one subspace is orthogonal (has a dot product of zero) with every vector in the other subspace. In the context of the script, the null space is perpendicular to the row space.
How does the script illustrate the concept of the zero vector in relation to subspaces?
-The zero vector is included as part of every subspace because it can be represented as a combination of the vectors in the subspace (e.g., 0 times any vector plus 0 times any other vector results in the zero vector).
What is the implication of the column space being the entire two-dimensional space in the given example?
-The implication is that the two columns of the matrix are independent, and their linear combinations can generate any vector in the two-dimensional space, leaving no room for additional vectors that would be part of the null space of A transpose in this particular example.
Outlines
📐 Introduction to Subspaces in Linear Algebra
Gilbert Strang introduces the concept of subspaces within the broader context of linear algebra. He clarifies that the current series of videos is not a comprehensive course on the subject but focuses on differential equations in relation to linear algebra. The big picture involves four subspaces, with an emphasis on understanding the column space and null space from a previous video. Strang then introduces the row space, defined by the vectors of a matrix and their linear combinations, which fill a plane in three-dimensional space. The null space is also discussed, characterized by vectors that, when multiplied by the matrix, yield the zero vector. Strang illustrates the null space as a line of vectors in a direction perpendicular to the row space, thus forming a right angle between these two subspaces.
📈 Exploring the Row Space and Null Space
The discussion continues with the exploration of the row space and null space. Strang explains that the row space is a plane formed by the linear combinations of two vectors, represented by the rows of a matrix. He demonstrates that this plane is filled by all possible combinations of these vectors. The null space is then described as an infinite line of vectors that are solutions to the equation Av = 0, where v is a vector. Strang shows that the null space is perpendicular to the row space, creating a 90-degree angle between these two subspaces. The concept of the column space is introduced next, which is the space spanned by all combinations of the matrix's columns. In the given example, the column space encompasses the entire two-dimensional space, as the first two columns are independent and their combinations cover the entire plane.
🔍 Transposing Matrices to Understand Subspaces
Strang elaborates on the relationship between the row space and the column space by transposing the matrix. He points out that by transposing, the row space of the original matrix becomes the column space of the transposed matrix. He emphasizes the elegance of linear algebra by stating that if you have the column space and null space of a matrix A, and the column space of A's transpose, the fourth subspace is naturally the null space of A's transpose. In the given example, the null space of A's transpose is found to be trivial, containing only the zero vector, thus referred to as the '0 subspace.' Strang notes that in other examples, all four subspaces could be non-zero, but in this case, the column space occupies the entirety of R2, leaving no room for the null space of A's transpose.
📊 Dimensionality and the Rank of Subspaces
The final paragraph delves into the dimensions of the four subspaces and the concept of the rank of a matrix. Strang explains that the dimension of the row space is equal to the rank of the matrix, denoted as R, which is the number of independent rows. He highlights the important property that the column space and the row space share the same dimension, meaning the number of independent rows equals the number of independent columns. For the null space and the left null space, their dimensions are the remaining dimensions after accounting for the rank. Specifically, the null space has a dimension of N - R, and the left null space has a dimension of M - R, where N and M are the dimensions of the original matrix. Strang concludes by noting that he will discuss the concept of dimension in more detail in a separate video.
Mindmap
Keywords
💡Linear Algebra
💡Subspaces
💡Column Space
💡Row Space
💡Null Space
💡Linear Combinations
💡Dot Product
💡Transpose of a Matrix
💡Null Space of A Transpose
💡Rank of a Matrix
💡Dimension
Highlights
Linear algebra is presented in the context of subspaces, with a focus on the big picture rather than a full course.
The concept of the column space and null space is introduced, with the column space defined by the matrix's columns and the null space by solutions to Av=0.
The row space is explained as the set of all linear combinations of a matrix's rows, visualized as a plane in three-dimensional space.
The null space is described as an infinite line of vectors, which is a one-dimensional subspace, and is perpendicular to the row space.
The dot product is used to demonstrate the perpendicularity between the null space and the row space.
The column space of a matrix is shown to be the entire two-dimensional space when the matrix's columns are independent.
The fourth subspace, the null space of the transposed matrix (A^T), is introduced and shown to be the 0 subspace in the given example.
The concept of transposing a matrix is used to connect the row space of the original matrix to the column space of its transpose.
The rank of a matrix (R) is identified as a key number, representing the dimension of the row space and the column space.
The relationship between the dimensions of the four subspaces is explained, with the null space and left null space having dimensions N-R and M-R, respectively.
The video emphasizes the elegance of linear algebra through the relationships between the four fundamental subspaces.
The importance of understanding the rank of a matrix is highlighted as it relates to the number of independent rows and columns.
An example is used to illustrate how the column space of a 2x3 matrix fills all of R^2, leaving no room for the left null space.
The video concludes with a summary sketch of the four subspaces in their respective dimensional spaces, emphasizing their perpendicular relationships.
The concept of dimension is teased for further exploration in a separate video, indicating the depth of the topic.
The educational approach focuses on visualizing abstract algebraic concepts, making them more accessible for learners.
The use of practical examples, such as the 2x3 matrix, helps to clarify complex mathematical principles.
Transcripts
Browse More Related Video

Order, Dimension, Rank, Nullity, Null Space, Column Space of a matrix

Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra

Least squares approximation | Linear Algebra | Khan Academy
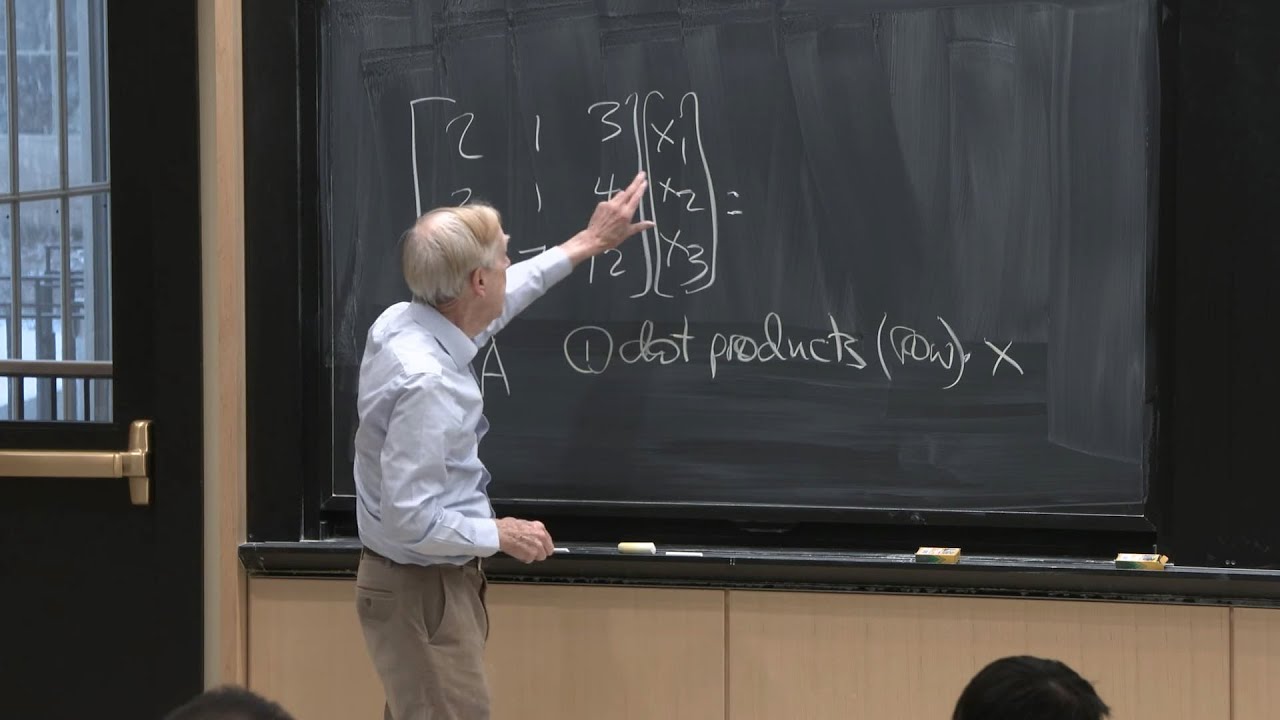
Lecture 1: The Column Space of A Contains All Vectors Ax

Subspaces and Span

Dear linear algebra students, This is what matrices (and matrix manipulation) really look like
5.0 / 5 (0 votes)
Thanks for rating: