PROJECTILE MOTION RELATED DERIVATIONS | TIME OF FLIGHT | HORIZONTAL RANGE | MAXIMUM HEIGHT | KANNADA

EDUcare Light For Life

15 Jul 202325:51

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses the physics of projectile motion, focusing on the concepts of velocity, angle of projection, and the equations governing the motion. It explains how the initial velocity along the y-axis and the gravitational force affect the projectile's maximum height and range. The script also delves into the time taken for the projectile to reach its peak and return to Earth's surface, emphasizing the symmetry of ascent and descent. Mathematical expressions are provided to calculate these parameters, offering a comprehensive understanding of the dynamics involved in projectile motion.

Takeaways

📐 The projectile's angle with the x-axis is denoted as Theta.
🏹 Initial velocity components are considered along the x and y axes.
📈 The velocity along the y-axis at maximum height is zero.
🚀 The time taken to reach maximum height (TM) can be calculated using the initial velocity and gravitational force.
🔄 The time of ascent to maximum height is equal to the time of descent.
📊 The total time of flight (T) is twice the time taken to reach maximum height.
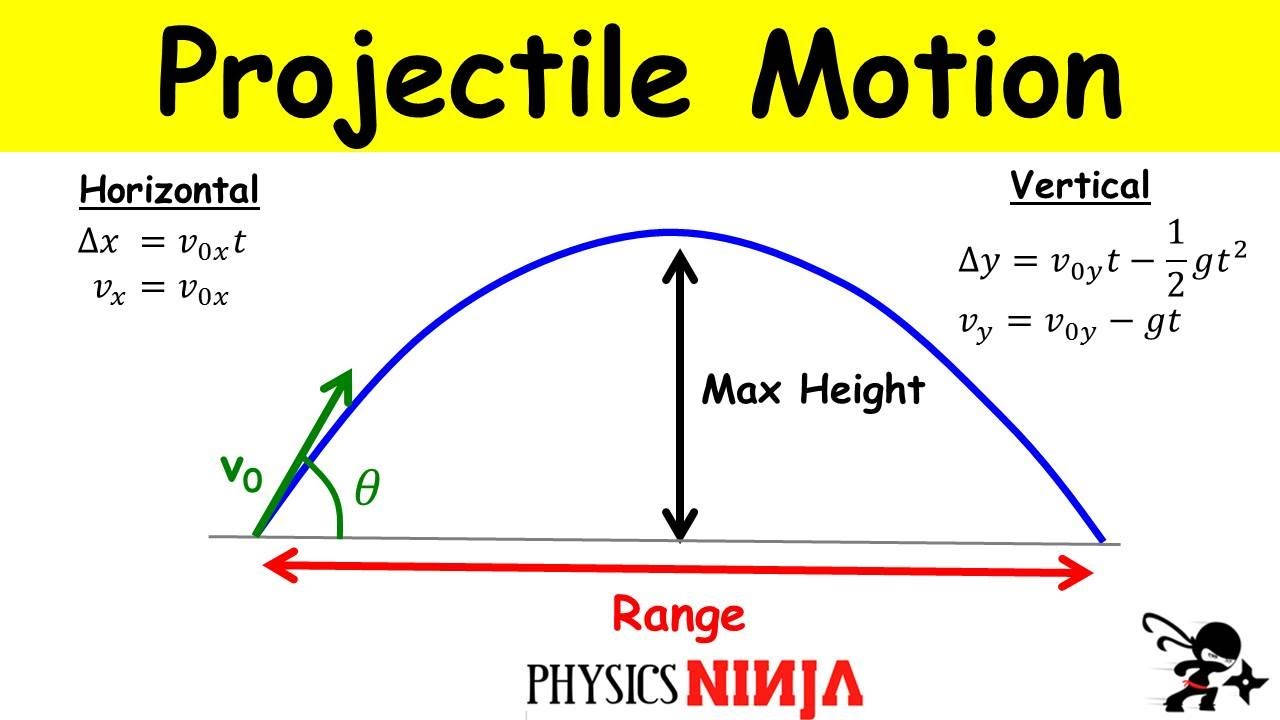
📈 The maximum height reached by the projectile can be calculated using the initial velocity and angle Theta.
🎯 The horizontal range along the x-axis is determined by the initial velocity and angle Theta.
🔢 The displacement along the x-axis is given by the formula s = Vnot * t + 0.5 * a * t^2.
🔝 The vertical displacement along the y-axis is given by the formula h = Vnot_y * t - 0.5 * g * t^2.
🌐 The projectile's trajectory is influenced by its initial velocity (Vnaught) and the angle (Theta) with respect to the positive x-axis.

Q & A

What is the significance of the angle Theta in projectile motion?
-The angle Theta determines the trajectory of the projectile and influences the range, height, and time of flight of the object. It is the angle the projectile makes with the positive x-axis along the positive y-axis at the moment of launch.
What is the initial velocity component along the y-axis in terms of the initial velocity and angle Theta?
-The initial velocity component along the y-axis, often denoted as V_not_y, is given by the product of the initial velocity (V_not) and the sine of angle Theta (sin(Theta)). This component is critical for determining the maximum height reached by the projectile.
At what point does the projectile's velocity along the y-axis become zero?
-The projectile's velocity along the y-axis becomes zero at its maximum height. At this point, the vertical component of the velocity is zero before it starts to accelerate downwards due to gravity.
What is the relationship between the time taken to reach maximum height (TM) and the initial velocity and angle Theta?
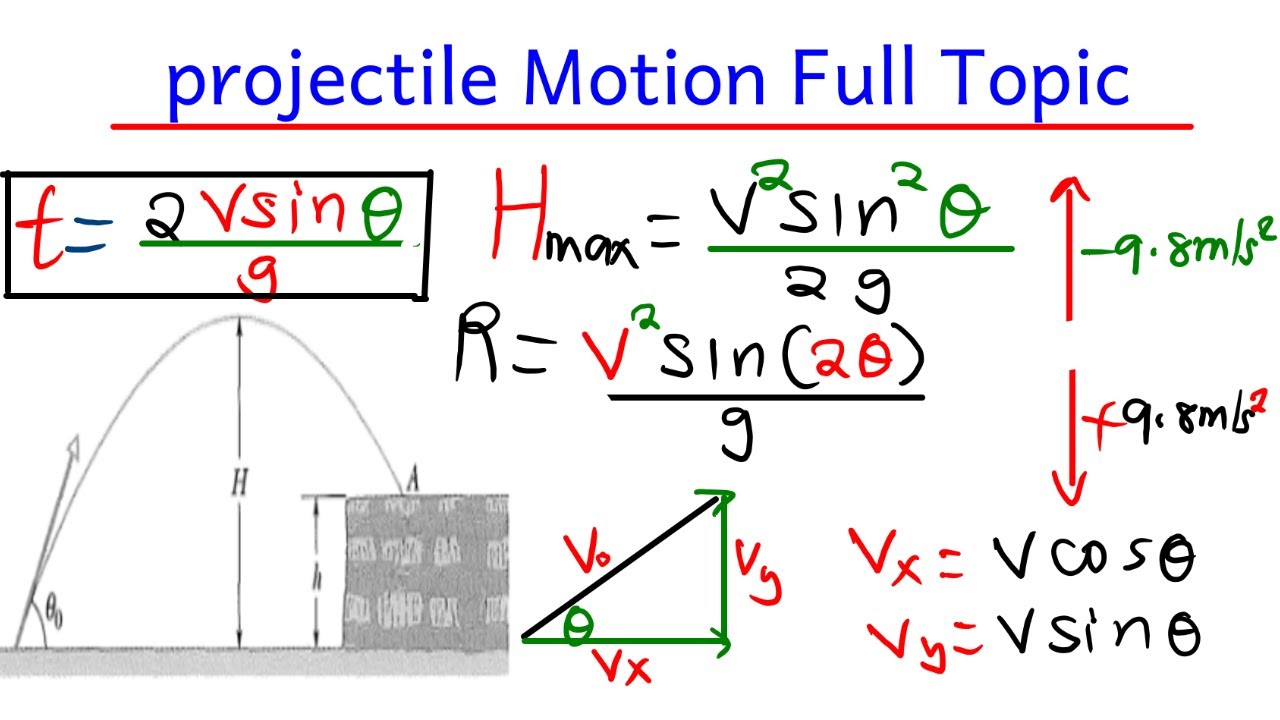
-The time taken to reach maximum height (TM) is given by the equation TM = V_not * sin(Theta) / g, where g is the acceleration due to gravity. This equation shows that the time to reach the maximum height is directly proportional to the initial velocity's y-component and the sine of the launch angle.
How is the maximum height reached by the projectile calculated?
-The maximum height (h) is calculated using the formula h = (V_not^2 * sin^2(Theta)) / (2 * g). This formula takes into account the initial velocity, the square of the sine of the launch angle, and the acceleration due to gravity.
What is the significance of the time of ascent and time of descent in projectile motion?
-The time of ascent and time of descent are significant because they are equal for an object in projectile motion, assuming no air resistance. This symmetry is due to the fact that the only force acting on the object after launch is gravity, which affects the upward and downward motion in the same way.
What is the total time of flight for a projectile?
-The total time of flight (T) for a projectile is the sum of the time taken to reach maximum height and the time taken to descend from the maximum height to the Earth's surface. It is given by the equation T = 2 * TM, which simplifies to T = 2 * V_not * sin(Theta) / g.
What is the horizontal range of a projectile, and how is it calculated?
-The horizontal range is the total distance a projectile travels along the x-axis before it hits the ground. It can be calculated using the formula R = 2 * V_not * sin(Theta) * cos(Theta) / g, where V_not is the initial velocity, Theta is the launch angle, and g is the acceleration due to gravity.
How does air resistance affect the projectile motion equations?
-Air resistance can significantly alter the projectile motion by introducing additional forces that were not accounted for in the ideal projectile motion equations. In real-world scenarios, air resistance can decrease the range, affect the trajectory, and change the time of flight of the projectile. However, in the provided script, air resistance is neglected, and the motion is considered ideal.
What is the role of gravitational force in projectile motion?
-Gravitational force is the only force acting on the projectile after it is launched, assuming air resistance is negligible. It causes the projectile to accelerate downwards at a rate of g (approximately 9.81 m/s^2 on Earth), affecting the vertical component of the motion and ultimately determining the maximum height, time of flight, and range of the projectile.
How does the initial velocity's magnitude (V_not) affect the projectile's trajectory?
-The magnitude of the initial velocity (V_not) directly influences the projectile's speed and distance traveled. A higher initial velocity results in a longer range, a greater maximum height, and a longer time of flight. The trajectory of the projectile is also affected, with a higher initial velocity leading to a flatter parabolic path.
What is the equation for displacement in projectile motion?
-The displacement in projectile motion is given by the kinematic equation s = ut + (1/2)at^2 for the y-axis, where u is the initial velocity component along the y-axis, a is the acceleration due to gravity (negative in the y-direction), and t is the time. For the x-axis, the displacement x = V_not * cos(Theta) * t, as there is no acceleration in the horizontal direction.

Outlines

00:00

📐 Projectile Motion: Angle and Velocity Components

This paragraph introduces the concept of projectile motion, focusing on the angle (Theta) that the projectile makes with the x-axis and its implications on velocity components. It explains that the projectile's velocity along the y-axis is a critical factor in determining its maximum height. The paragraph also touches on the velocity at maximum height, which is zero, and the initial velocity components along the y-axis, represented as V naught sine Theta.

05:34

🧮 Equations of Motion at Maximum Height

The second paragraph delves into the mathematical equations governing a projectile's motion at its maximum height. It establishes the equation for the object's velocity along the Y axis, highlighting that the final velocity (V final) at maximum height equals the initial velocity (V naught) along the y-axis. The paragraph also discusses the time (TM) it takes for the projectile to reach this maximum height and how it relates to the initial velocity and gravitational force. The key equation presented is 0 = V not sin Theta - gt, which shows the balance of forces at the maximum height.

11:04

🕒 Time of Ascent and Descent in Projectile Motion

This paragraph focuses on the time aspects of projectile motion, explaining that the time taken to reach the maximum height (ascent) is equal to the time taken to descend back to the Earth's surface (descent). It introduces the concept of time of flight (T), which is the total time from launch to landing, and provides the expression T = 2 * (V naught sine Theta) / G. The paragraph also briefly touches on the displacement along the Y axis and the initial velocity component along the Y axis.

16:05

📈 Calculating the Range of a Projectile

The fourth paragraph discusses the calculation of a projectile's horizontal range, which is the distance it travels along the x-axis. It presents the equation T^2 = 2 * (V naught^2 * sine^2 Theta) / G, derived from the previous discussions on time of flight and initial velocity. This equation is crucial for understanding the factors that affect the horizontal range of a projectile and how they can be manipulated to achieve desired outcomes.

21:07

🌐 Projectile Range and Gravitational Influence

The final paragraph builds upon the previous discussions to provide a comprehensive understanding of the projectile's horizontal range. It introduces the expression 2 * V naught * sine Theta / GM, which calculates the distance traveled along the x-axis. This equation takes into account the gravitational force (GM) and shows how it influences the projectile's range. The paragraph emphasizes the importance of understanding these calculations for practical applications of projectile motion.

Mindmap

Keywords

💡Projectile

A projectile is an object that is propelled through the air and follows a specific trajectory due to the forces acting upon it, such as gravity. In the context of the video, a projectile is launched with an initial velocity at an angle to the horizontal, and the discussion revolves around understanding its motion and the factors affecting it, such as the angle of launch and gravitational force.

💡Angle Theta

Angle Theta refers to the angle between the initial velocity of the projectile and the horizontal axis (x-axis). This angle is crucial in determining the trajectory of the projectile and how it will be influenced by gravity and air resistance. The larger the angle, the more the projectile will be affected by gravity, leading to a shorter range and a quicker descent.

💡Velocity

Velocity is a vector quantity that describes the speed of an object in a specific direction. In the context of the video, the velocity of the projectile is broken down into components along the x-axis and y-axis. The y-component of velocity is particularly important as it determines how high and how far the projectile will travel.

💡Acceleration

Acceleration is the rate of change of velocity of an object with respect to time. In the case of a projectile, the only acceleration acting on it (neglecting air resistance) is due to gravity, which is constant and directed downwards. This acceleration affects the projectile's vertical motion, causing it to slow down as it ascends and speed up as it descends.

💡Maximum Height

The maximum height is the highest point reached by the projectile during its trajectory. This occurs when the vertical component of the projectile's velocity becomes zero, as the object momentarily stops ascending before descending back to the ground. The maximum height is influenced by the initial velocity and the angle of launch.

💡Time of Ascent

Time of ascent refers to the time interval during which the projectile is moving upwards, from the moment of launch until it reaches its maximum height. This time is crucial in understanding the total flight time of the projectile and can be calculated using the initial velocity and the acceleration due to gravity.

💡Horizontal Range

Horizontal range is the distance a projectile travels along the horizontal axis (x-axis) before landing. It is determined by the initial velocity, the angle of launch, and the time the projectile is in the air. The greater the initial velocity and the higher the angle, the longer the horizontal range.

💡Kinematic Equations

Kinematic equations are mathematical formulas used to describe the motion of an object under constant acceleration, such as a projectile in free fall. These equations relate displacement, velocity, time, and acceleration, allowing us to predict the behavior of the projectile throughout its flight.

💡Initial Velocity (V naught)

Initial velocity, often denoted as V naught, is the speed at which the projectile is launched. It is a critical factor in determining the trajectory and range of the projectile. The initial velocity has both a magnitude and a direction, with components along the x-axis and y-axis that influence the projectile's motion in each dimension.

💡Gravitational Force (g)

Gravitational force, denoted as g, is the attractive force that Earth exerts on objects, which near the surface is approximately 9.81 meters per second squared (m/s^2). This force acts vertically downward and affects the projectile's motion by causing it to accelerate downwards, thus influencing its ascent and descent.

💡Time of Flight

Time of flight is the total duration from the moment a projectile is launched until it lands. It includes both the time of ascent to the maximum height and the time of descent back to the ground. Understanding the time of flight is essential for analyzing the overall motion and trajectory of the projectile.

Highlights

Projectile motion is discussed with a focus on the angle Theta it makes with the x-axis.

The velocity component along the y-axis at maximum height is analyzed.

The initial velocity along the y-axis is determined by the initial velocity and the angle Theta.

The equation for the final velocity at maximum height is given as V_final = V_0 * sin(Theta).

The time taken by the projectile to reach maximum height (TM) is derived from the given equations.

The relationship between the time of ascent and descent in projectile motion is discussed, showing they are equal.

The total time of flight (T) is expressed as 2 * TM, which is a combination of the times of ascent and descent.

The mathematical expression for the maximum height reached by the projectile is provided.

The horizontal range of the projectile is defined and calculated using the initial velocity and the angle Theta.

The displacement along the y-axis is related to the initial velocity and the time of flight.

The concept of gravitational force acting as the center of the Earth is introduced.

The equation for the displacement along the x-axis (horizontal range) is detailed, involving the initial velocity and the angle Theta.

The significance of the angle Theta in determining the trajectory and range of the projectile is emphasized.

The comprehensive kinematic equations for projectile motion are presented, including those for the x and y axes.

The practical applications of understanding projectile motion, such as in sports and military strategies, are alluded to.

The transcript provides a detailed analysis of the physics behind projectile motion, which is crucial for further studies and real-world applications.

The innovative methods of solving projectile motion problems using the given angles and velocities are discussed.

Transcripts

Browse More Related Video

Projectile Motion Maximum Height Formula Derivation

Projectile Motion: Finding the Maximum Height and the Range

Projectile Motion (of an Object Fired at an Angle) - A Level Physics

NEET Physics | Projectile Motion | Theory & Problem-Solving | In English | Misostudy

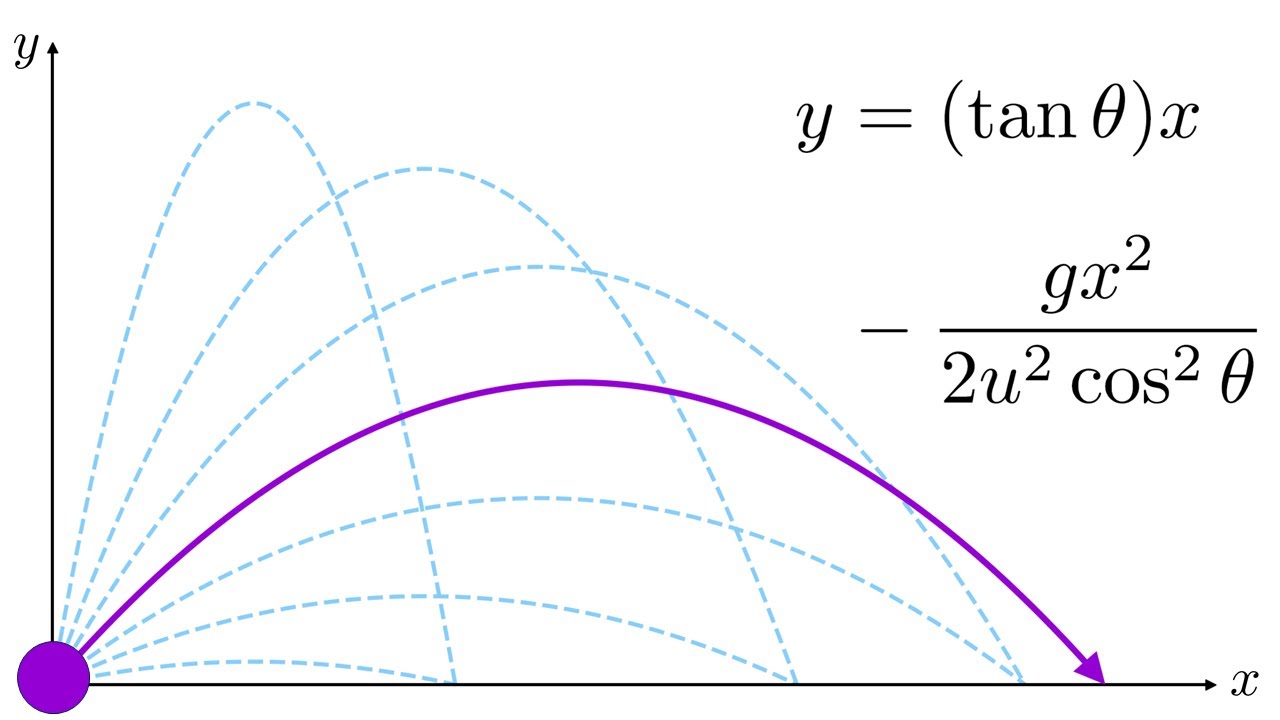
Trajectory of a projectile without drag

projectile motion Recorded class

Related Tags

Projectile Motion Physics Concepts Kinematic Equations Angle Theta Maximum Height Horizontal Range Velocity Analysis Gravitational Force Time of Ascent Time of Descent