NEET Physics | Projectile Motion | Theory & Problem-Solving | In English | Misostudy
TLDRIn this educational video, the concept of projectile motion is explored, focusing on the parabolic trajectory of a particle launched at an angle to the horizontal. The video delves into the components of initial velocity in both horizontal and vertical directions, the role of gravitational acceleration, and how these factors contribute to the particle's maximum height, range, and time of flight. Key formulas are derived for calculating these parameters, and the equation of the projectile's trajectory is established. The video also discusses special cases, such as the symmetric range for complementary angles of projection, providing a comprehensive understanding of two-dimensional motion.
Takeaways
- 🎯 The class discusses projectile motion, a special type of two-dimensional motion where an object follows a parabolic trajectory.
- 📐 In projectile motion, the initial velocity has two components: horizontal (u*cos(theta)) and vertical (u*sine(theta)).
- 🌐 The only acceleration acting on the particle is gravity (G), which acts vertically downward.
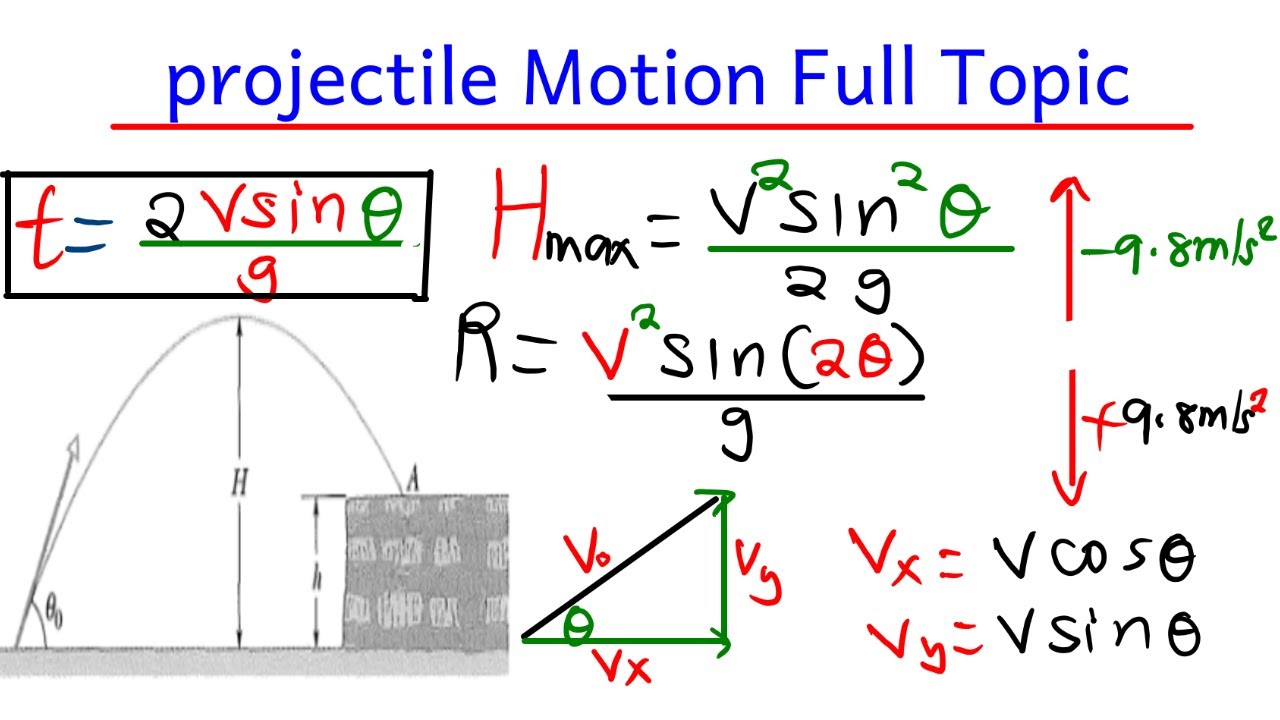
- 🚀 The maximum height (H) reached by the particle is given by the formula H = (u^2 * sin^2(theta)) / (2 * G).
- 🕰️ The time of flight (T) for the particle to return to its initial height is T = 2 * (u * sin(theta)) / G.
- 🏹 The range (X), or maximum horizontal displacement, is calculated using X = (u^2 * sin(2*theta)) / G.
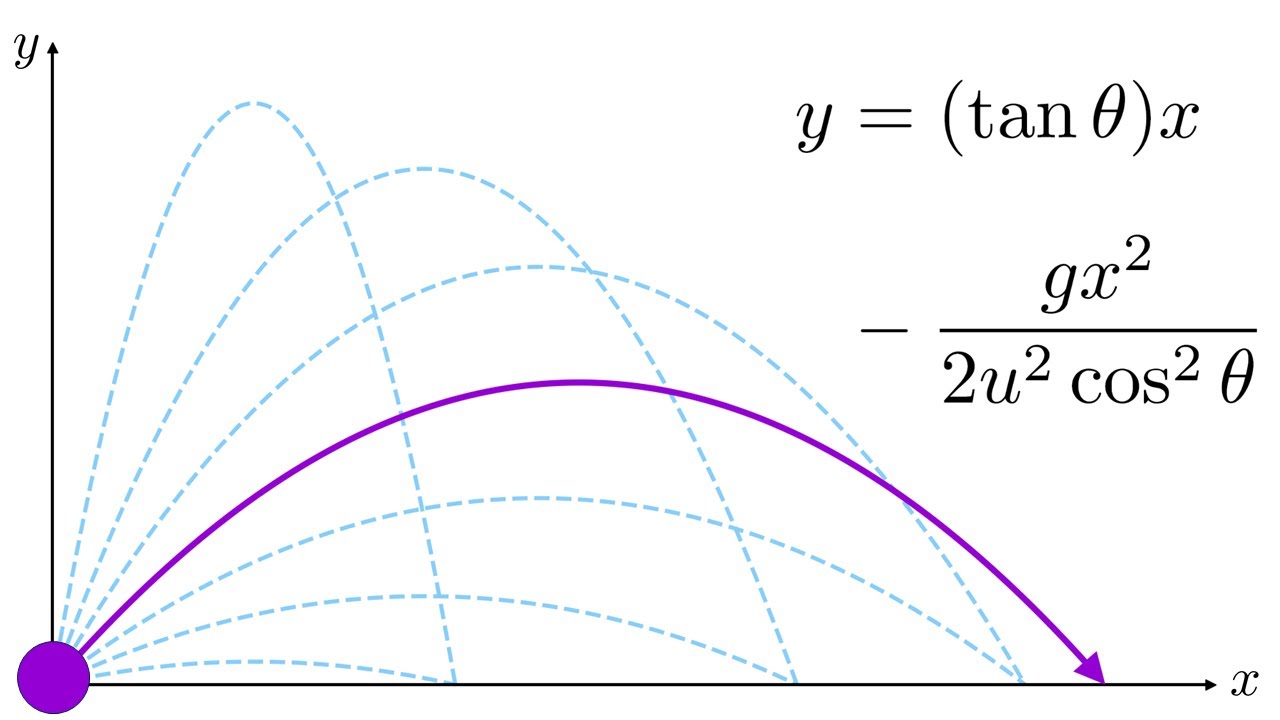
- 📈 The equation of the trajectory of the projectile is derived as y = (X * tan(theta)) - (1/2 * G * X^2) / (u^2 * cos^2(theta)).
- 🔄 The time to reach the maximum height is half the time of flight (T_max = T/2).
- 🔄 For two angles of projection that are complementary (summing to 90 degrees), the range will be the same if the initial velocity is also the same.
- 🔢 The change in momentum of the particle at its highest point can be calculated using the principle of conservation of momentum, taking into account the initial and final velocities.
Q & A
What is the definition of projectile motion?
-Projectile motion is a special type of two-dimensional motion where an object is launched into the air with an initial velocity at a certain angle to the horizontal, and it moves under the influence of gravity alone, following a parabolic trajectory.
How does the initial velocity of a projectile influence its motion?
-The initial velocity of a projectile has two components: one along the horizontal direction (u*cos(theta)) and one along the vertical direction (u*sine(theta)). These components determine the object's speed and direction at any point during its trajectory.
What is the significance of the angle of projection in projectile motion?
-The angle of projection (theta) affects the trajectory of the projectile, the range (horizontal distance traveled), the maximum height reached, and the time of flight. The angle determines the balance between the horizontal and vertical components of the initial velocity.
What is the only force acting on a projectile in motion?
-The only force acting on a projectile in motion is gravity, which pulls the object downward with an acceleration of 'g' (approximately 9.81 m/s^2 on Earth).
How can you calculate the time of flight of a projectile?
-The time of flight (T) of a projectile can be calculated using the formula T = 2*u*sin(theta)/g, where 'u' is the initial velocity, 'theta' is the angle of projection, and 'g' is the acceleration due to gravity.
What is the maximum height (H_max) reached by a projectile?
-The maximum height (H_max) reached by a projectile can be calculated using the formula H_max = (u^2*sin^2(theta))/(2*g), where 'u' is the initial velocity and 'g' is the acceleration due to gravity.
What is the range (X) of a projectile?
-The range (X) of a projectile, which is the maximum horizontal distance it travels before landing, can be calculated using the formula X = (u^2*sin(2*theta))/(g), where 'u' is the initial velocity and 'theta' is the angle of projection.
What is the equation of the trajectory of a projectile?
-The equation of the trajectory (y versus x) of a projectile is given by y = (x*tan(theta) - (g*x^2)/(2*u^2*cos^2(theta))). This equation describes the parabolic path followed by the projectile.
How does the time to reach the highest point compare to the total time of flight in projectile motion?
-The time to reach the highest point (t_H) is half of the total time of flight (T). It can be calculated using the formula t_H = u*sin(theta)/g, which is half of the formula for the total time of flight T = 2*u*sin(theta)/g.
What happens to the momentum of a projectile at its highest point?
-At the highest point of projectile motion, the vertical component of the velocity becomes zero, but the horizontal component remains constant (u*cos(theta)). Therefore, the change in momentum is only in the vertical direction, and it is equal to the initial vertical momentum (mu*sin(theta)) subtracted from the final vertical momentum (which is zero).
How does the range of a projectile change if the angle of projection is complementary?
-If the angle of projection and another angle (theta_1) are complementary (theta + theta_1 = 90 degrees), and the initial velocity is the same for both angles, the range of the projectile will be the same for both angles. This is because the range formula X = (u^2*sin(2*theta))/(g) becomes X = (u^2*sin(2*(90-theta)))/(g), which simplifies to the same expression for range.
Outlines
📚 Introduction to Projectile Motion
This paragraph introduces the concept of projectile motion, a special type of two-dimensional motion. It explains how an object, such as a chalk holder, moves through space following a parabolic path when projected at an angle. The initial velocity is broken down into its horizontal (U cos theta) and vertical (U sine theta) components. The paragraph also discusses the maximum height and range of the projectile, emphasizing that the only acceleration acting on the particle is gravity (G), which acts vertically downward.
🕒 Time of Flight and Range Calculations
This section delves into the specifics of calculating the time of flight and range of a projectile. It explains how to determine the time it takes for the projectile to hit the ground (capital T) using the formula T = 2U sine theta by G. The maximum horizontal displacement, or range (capital X), is derived using the formula X = U square sine 2 theta by G. Additionally, the paragraph discusses the method to find the time taken to reach the highest point, which is half the time of flight.
📈 Equations for Projectile Motion
This paragraph focuses on the mathematical equations governing projectile motion. It provides the equations for maximum height (H max = u square sine square theta by 2 G) and explains the conditions under which the range is maximized. The special case where the angle of projection is 45 degrees is highlighted, as it yields the maximum range. The paragraph also introduces the equation for the trajectory of the projectile, which relates the horizontal displacement (X) and vertical displacement (Y) as y = X tan theta - 1/2 G X square upon u square, cos square theta.
🔄 Complementary Angles and Range
This part of the script explores the relationship between complementary angles of projection and their effect on the range of a projectile. It explains that if two angles are complementary (summing up to 90 degrees) and the initial velocity is the same, the range of the projectile will be the same for both angles. This concept is illustrated with an example where projecting at angles theta and 90 - theta results in the same range, provided the initial velocity is identical.
🚀 Change in Momentum at the Highest Point
The final paragraph shifts focus to a practical question regarding the change in momentum of a projectile at its highest point. The momentum change is calculated by considering the initial and final velocities of the particle at the highest point. The initial velocity is given as U cos theta, and at the highest point, the vertical velocity becomes zero, leaving only the horizontal component of velocity. This question sets the stage for applying the concepts learned in the previous paragraphs to solve real-world physics problems related to projectile motion.
Mindmap
Keywords
💡Projectile Motion
💡Initial Velocity
💡Acceleration
💡Parabolic Trajectory
💡Horizontal and Vertical Displacement
💡Time of Flight
💡Range
💡Maximum Height
💡Components of Velocity
💡Equation of Trajectory
Highlights
Introduction to projectile motion, a special kind of two-dimensional motion.
Description of the parabolic trajectory of a projectile.
The initial velocity has two components: horizontal (u cos theta) and vertical (u sine theta).
The only acceleration acting on the projectile is gravity (G), acting vertically downward.
The maximum height (H) reached by the projectile can be calculated using the formula H = u^2 * sin(2theta) / (2G).
The range (maximum horizontal displacement) of the projectile is given by X = u^2 * sin(2theta) / G.
The time of flight (T) for the projectile to hit the ground again is T = 2 * u * sin(theta) / G.
At the highest point, the vertical component of velocity becomes zero.
Equation of the trajectory of the projectile derived as y = X * tan(theta) - (1/2) * G * X^2 / (u^2 * cos^2(theta)).
The time taken to reach the highest point is half the total time of flight.
For projectile motion, the motion is broken down along the x and y axes to simplify analysis.
No acceleration acts on the projectile in the horizontal direction.
The horizontal component of the initial velocity (u cos theta) determines the range of the projectile.
The vertical component of the initial velocity (u sine theta) influences the maximum height reached by the projectile.
The time of flight can be calculated using the initial velocity and the acceleration due to gravity.
Understanding projectile motion is crucial for applications in physics and engineering, such as in sports and projectile launching.
The relationship between the angle of projection and the range and maximum height of the projectile is highlighted.
If the angle of projection is changed to its complementary angle, the range of the projectile remains the same, assuming the same initial velocity.
The lecture provides a comprehensive overview of the fundamental concepts and equations related to projectile motion.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: