projectile motion Recorded class

Transcended Institute

30 May 202370:44

EducationalLearning

32 Likes 10 Comments

TLDRThe transcript discusses the concept of projectile motion, focusing on the two-dimensional movement of objects in the X and Y directions. It explains three cases of projectile motion: throwing from a building, from the ground at an angle, and a combination of both. The formulas for calculating height, time, and range are derived, with emphasis on the importance of the angle for maximum range. The impact of initial velocity, gravitational acceleration, and time on the object's trajectory is analyzed. The transcript also addresses common questions about finding maximum height, total time in the air, and velocity upon impact.

Takeaways

📐 Projectile motion involves an object moving in two dimensions, with linear motion in the X direction and free fall motion in the Y direction.
🌟 There are three cases of projectile motion: throwing from the top of a building, throwing from ground level at an angle, and throwing from ground level straight upwards.
📈 The formula for the height of a building in the first case is H = (1/2) * g * t^2, where g is the acceleration due to gravity and t is the time.
🕒 The time it takes for an object to reach the ground from the top of a building is given by t = √(2H/g), where H is the height of the building.
🏆 The range (horizontal distance) of an object thrown from the top of a building is calculated by R = (v_x * t), with v_x being the constant horizontal velocity.
🎯 For an object thrown at an angle from the ground, the maximum range is achieved when the angle is 45 degrees.
🚀 The formula for the maximum height reached by an object thrown at an angle is H_max = (v^2 * sin^2(θ)) / (2 * g), where v is the initial velocity and θ is the angle of projection.
🕝 The range of an object thrown at an angle can be found using R = (v * cos(θ) * t), with t being the total time in air.
🔄 In the third case of projectile motion (thrown from a height at an angle), the total time in air is the sum of the time to reach the maximum height and the time to fall back down.
📌 The final velocity of an object just before it hits the ground can be calculated by combining the constant horizontal velocity (v_x = v * cos(θ)) with the vertical velocity (v_y = v * sin(θ) - g * t).
🔢 Solving projectile motion problems requires understanding and applying kinematic equations, including the influence of gravity (g) on the object's motion.

Q & A

What is projectile motion?
-Projectile motion refers to the motion of an object in two dimensions when it is moving in the X-direction (horizontally) and Y-direction (vertically) simultaneously, typically under the influence of gravity.
What are the three cases of projectile motion mentioned in the script?
-The three cases of projectile motion discussed are: 1) An object thrown from the top of a building and falling to the ground. 2) An object thrown from the ground at an angle and reaching its maximum height. 3) A combination of the first two cases, where an object is thrown at an angle from the ground, reaches its maximum height, and then falls to the ground.
How is the height of a building calculated in the first case of projectile motion?
-In the first case, the height of the building (h) can be calculated using the formula: h = (1/2) * g * t^2, where g is the acceleration due to gravity (9.8 m/s^2) and t is the time the object takes to fall to the ground.
What is the formula to find the time it takes for an object to reach its maximum height in the second case of projectile motion?
-The time (t) it takes for an object to reach its maximum height in the second case can be found using the formula: t = (2 * h) / g, where h is the maximum height and g is the acceleration due to gravity.
How do you calculate the range in the second trajectory of projectile motion?
-The range (horizontal distance) in the second trajectory can be calculated using the formula: Range = v_x * t, where v_x is the constant horizontal velocity component and t is the total time the object is in the air.
What is the significance of the angle of 45 degrees in projectile motion?
-An angle of 45 degrees is significant because it allows for the maximum range when an object is thrown from the ground at an angle. This is due to the fact that the horizontal and vertical components of the initial velocity are equal at this angle, leading to the greatest possible distance traveled.
How is the maximum height calculated in the third trajectory of projectile motion?
-The maximum height (H_max) in the third trajectory can be calculated using the formula: H_max = (v^2 * sin^2(θ)) / (2 * g), where v is the initial velocity, θ is the launch angle, and g is the acceleration due to gravity.
What is the total time of flight for an object in the third trajectory of projectile motion?
-The total time of flight (T) for an object in the third trajectory can be found using the formula: T = (v * sin(θ)) / g + √(2 * H_max / g), where v is the initial velocity, θ is the launch angle, and H_max is the maximum height reached.
How do you find the velocity of a projectile just before it hits the ground?
-To find the velocity of a projectile just before impact, you calculate the horizontal velocity (V_x = v * cos(θ)) and the vertical velocity (V_y = v * sin(θ) - g * t) at the moment of impact. Then, use the Pythagorean theorem to find the resultant velocity: V = √(V_x^2 + V_y^2).
What is the relationship between the initial velocity and the velocity at maximum height in a projectile's trajectory?
-At the maximum height, the vertical component of the velocity is zero due to the object's temporary stop in its upward motion. The horizontal component of the velocity (V_x) remains constant throughout the trajectory. Therefore, the initial velocity (V) at the launch point is equal to the horizontal velocity (V_x) at maximum height.

Outlines

00:00

🚀 Introduction to Projectile Motion

This paragraph introduces the concept of projectile motion, explaining that it involves an object moving in two dimensions - horizontally (X direction) and vertically (Y direction). It clarifies that 'projectile' refers to the motion of an object in the X direction (linear motion) and 'free fall' to the motion in the Y direction. The paragraph also outlines three key cases of projectile motion and introduces the formulas used in free fall motion, emphasizing the difference in the acceleration due to gravity (G) and linear acceleration (M).

05:02

🏢 Case 1: Projectile Motion from a Building

This section delves into the first case of projectile motion where an object is thrown from the top of a building. It discusses the initial conditions, such as zero initial velocity and the height of the building (h). The paragraph explains how to calculate the height of the building (H) using the formula D = V_initial * t + 0.5 * G * t^2, where D is the distance, V_initial is the initial velocity (zero in this case), G is the acceleration due to gravity, and t is the time. It also touches on the concept of range (horizontal distance) and how it's affected by the value of G depending on the direction of motion (up or down).

10:02

🕰️ Formulas for Time, Height, and Range

This paragraph focuses on deriving formulas for time, height, and range in the context of projectile motion. It explains how to find the time it takes for an object to fall from a height (using the formula t^2 = 2H/G), the horizontal distance or range (given by the formula D = Vx * t, where Vx is the constant horizontal velocity), and the height of a building from which an object is thrown (using the formula H = 0.5 * GT^2, where G is gravity and T is the total time in the air). The paragraph emphasizes the importance of understanding these formulas for solving problems related to projectile motion.

15:05

📈 Case 2: Projectile Motion from the Ground

The second case explores projectile motion from the ground, introducing an object thrown at an angle (Theta). The paragraph explains the decomposition of the initial velocity into its horizontal (Vx = V * cos(Theta)) and vertical (Vy = V * sin(Theta)) components. It discusses the concept of maximum height (hmax) and how to calculate it using the formula hmax = V^2 * sin^2(Theta) / (2 * G). The paragraph also covers the time of flight, which is twice the time it takes to reach the maximum height, and how to find the range by considering the horizontal velocity and total time in the air.

20:06

🎯 Case 3: Combined Trajectory of Projectile Motion

The final case presented is the combined trajectory of projectile motion, which is a mix of the first two cases. This paragraph explains how to calculate the total time of flight, maximum height, and range for an object thrown at an angle from the ground. It introduces the formula for total time (T = V * sin(Theta) / G + sqrt(2 * H_max / G)), where H_max is the maximum height reached. The paragraph also discusses how to find the range by considering the horizontal velocity (Vx = V * cos(Theta)) and the total time of flight. The explanation includes the importance of understanding the components of velocity and how they contribute to the overall motion of the projectile.

25:06

📌 Solving Projectile Motion Problems

This paragraph wraps up the discussion on projectile motion by providing a step-by-step approach to solving related problems. It emphasizes the importance of identifying the type of trajectory (first, second, or combined) and applying the appropriate formulas for maximum height, range, and time of flight. The paragraph also encourages the audience to ask questions and engage with the material to ensure a comprehensive understanding of projectile motion and its applications.

Mindmap

Keywords

💡Projectile Motion

Projectile motion refers to the movement of an object that is propelled through the air and is influenced only by gravity. In the context of the video, it is the main subject being discussed, with the object moving in both horizontal (X direction) and vertical (Y direction) axes, creating a parabolic trajectory.

💡Linear Motion

Linear motion is a type of motion where an object moves along a straight path. In the video, linear motion is used to describe the horizontal component of projectile motion, where the object moves in the X direction with constant velocity,不受外力影响。

💡Free Fall Motion

Free fall motion is the motion of an object falling under the influence of gravity alone. In the video, free fall motion is discussed in relation to the vertical component of projectile motion, where the object moves in the Y direction and is affected by gravity,导致其加速度为9.8 m/s^2。

💡Acceleration Due to Gravity (G)

Acceleration due to gravity (G) is the acceleration experienced by an object due to the Earth's gravitational force. In the video, G is consistently used in the equations to calculate the vertical motion of the projectile, with a value of 9.8 meters per second squared (m/s^2).

💡Trajectory

A trajectory is the path followed by an object in motion. In the video, the trajectory is central to understanding projectile motion, as it describes the parabolic path of the object thrown in both horizontal and vertical directions.

💡Initial Velocity (V0)

Initial velocity (V0) is the speed at which an object starts moving. In the video, the initial velocity is a crucial factor in determining the trajectory and range of the projectile motion, as it defines the object's starting speed in both horizontal and vertical directions.

💡Range

Range in the context of projectile motion refers to the horizontal distance an object travels before landing. In the video, the range is calculated using the initial velocity in the horizontal direction and the time of flight.

💡Time of Flight

Time of flight is the total time an object is in the air during projectile motion. In the video, the time of flight is essential for calculating the range and other aspects of the motion, as it is determined by the vertical component of the motion.

💡Maximum Height

Maximum height is the highest point reached by an object in projectile motion. In the video, finding the maximum height involves using the initial velocity and the acceleration due to gravity in specific equations.

💡Velocity Components

Velocity components refer to the individual horizontal (Vx) and vertical (Vy) speeds of an object in projectile motion. In the video, the components are used to analyze the motion along each axis separately and to calculate various aspects of the projectile's path.

💡Equations of Motion

Equations of motion are mathematical formulas used to describe and predict the behavior of an object in motion. In the video, these equations are essential for calculating the different aspects of projectile motion, such as range, time of flight, and maximum height.

Highlights

Projector motion is the study of an object moving in two dimensions, with linear motion in the X direction and free fall motion in the Y direction.

In projectile motion, there are three cases to understand: throwing from the top of a building, throwing from ground level, and the combined trajectory which is a mix of the first two.

The first formula for projectile motion relates to the initial velocity, time, and gravitational acceleration (g), with final velocity being the initial velocity plus the product of g and time.

The second formula describes the distance (D) as a function of initial velocity (V), time (t), and gravitational acceleration (g), with D = V*t + 0.5*g*t^2.

The third formula for projectile motion relates the final squared velocity to the initial velocity squared, with the influence of gravity causing a change in the final velocity.

When an object is thrown from the top of a building, the initial velocity is zero, and the height (h) of the building can be calculated using the formula h = 0.5*g*t^2.

The time it takes for an object to reach its maximum height can be found using the formula t = V*sin(theta)/g, where theta is the angle of projection.

The maximum height (Hmax) reached by an object can be calculated with the formula Hmax = V^2*sin^2(theta)/(2*g), which depends on the initial velocity and the angle of projection.

The range (horizontal distance) of an object in projectile motion can be determined using the formula Range = V*cos(theta)*t, where V is the initial velocity and theta is the angle of projection.

In the combined trajectory of projectile motion, the total time of flight is the sum of the time to reach the maximum height and the time to descend from that height to the ground.

The final velocity of an object just before it hits the ground can be found by combining the horizontal and vertical components of velocity, using the initial velocity and time of flight.

To find the velocity of an object at its maximum height, one can use the formula Vx = V*cos(theta), where Vx remains constant throughout the motion and V is the initial velocity.

Understanding the influence of the angle of projection (theta) on the range and maximum height is crucial in applications such as sports and engineering.

Projectile motion can be analyzed using vector components, breaking down the motion into its horizontal (X direction) and vertical (Y direction) components for a more detailed understanding.

The concept of projectile motion is not only important in physics but also has practical applications in various fields, including military, sports, and entertainment.

Transcripts

Browse More Related Video

NEET Physics | Projectile Motion | Theory & Problem-Solving | In English | Misostudy

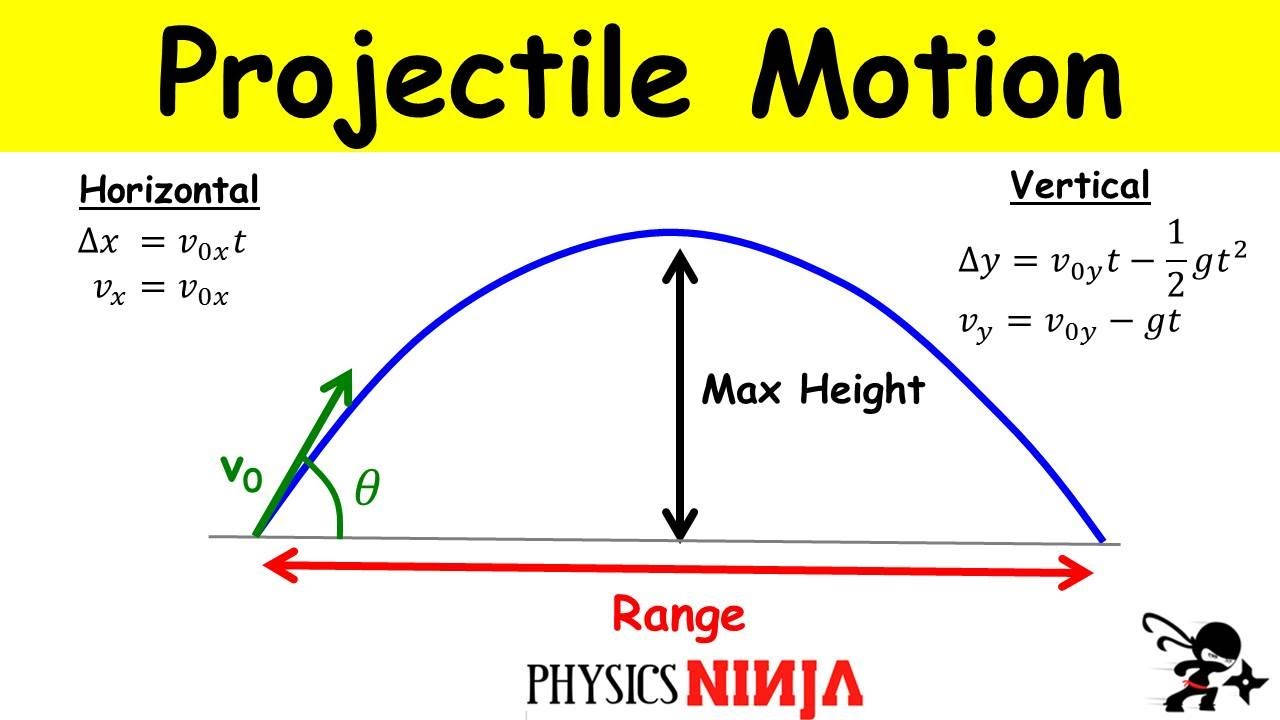
Projectile Motion: Finding the Maximum Height and the Range

Projectile Motion Maximum Height Formula Derivation

Regents Physics: Angled Projectile Problem Practice

PROJECTILE MOTION RELATED DERIVATIONS | TIME OF FLIGHT | HORIZONTAL RANGE | MAXIMUM HEIGHT | KANNADA

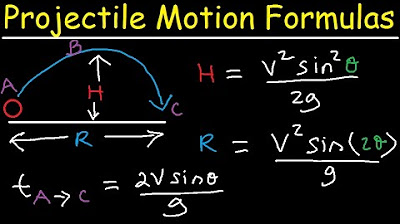
Introduction to Projectile Motion - Formulas and Equations

Related Tags

Physics Projectile Motion Linear Motion Free-Fall Equations Education Mathematics Kinematics Acceleration Mechanics