Impulse and Momentum - Formulas and Equations - College Physics

The Organic Chemistry Tutor
15 Nov 202315:24
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a comprehensive review of the concepts of impulse and momentum, essential for understanding classical mechanics. It introduces the fundamental formulas, including momentum as mass times velocity, impulse as force times time, and the impulse-momentum theorem. The script also explains how to calculate the force exerted by a fluid, the conservation of momentum in inelastic and elastic collisions, and the application of these principles to solve problems. The content is presented in a structured manner, making it accessible for students preparing for exams.

Takeaways
  • 📚 Momentum is calculated as the product of mass and velocity (p = mv).
  • 🚀 Impulse is the product of force and the time over which it acts (J = Ft).
  • 🔄 Impulse is equal to the change in momentum (Δp = FΔt = mΔv).
  • 🌊 Force can be described as the rate of change of momentum with respect to time (F = (mΔv)/Δt).
  • 💧 The force exerted by a fluid can be calculated using the formula F = (mass flow rate) * velocity (F = 𝑚̇ * v).
  • 🎯 In an inelastic collision, momentum is conserved but kinetic energy is not.
  • 🔄 The conservation of momentum states that the total momentum of a system before collision is equal to the total momentum after collision (p_initial = p_final).
  • 🏓 For perfectly elastic collisions, both momentum and kinetic energy are conserved.
  • 📌 When solving problems, use the appropriate equations based on the type of collision (inelastic or elastic) and the information provided.
  • 🔍 For complex problems, a system of equations may be required to solve for unknown variables.
Q & A

  • What is the definition of momentum?

    -Momentum is the product of an object's mass and velocity, and it is a vector quantity, meaning it has both magnitude and direction.

  • How do you calculate the momentum of an object?

    -To calculate the momentum of an object, you multiply its mass (kg) by its velocity (m/s). For example, a 10 kg object moving at 6 m/s has a momentum of 60 kg·m/s.

  • What is impulse and how is it calculated?

    -Impulse is the product of force and the time over which it acts. It is calculated by multiplying the force (in Newtons) applied to an object by the time interval (in seconds) during which the force is applied.

  • Explain the relationship between impulse and the change in momentum.

    -Impulse is equal to the change in momentum of an object. This means that when a force is applied to an object over a certain time period, the object's momentum changes by an amount equal to the impulse applied.

  • What is the Impulse-Momentum Theorem?

    -The Impulse-Momentum Theorem states that the impulse exerted on an object is equal to the change in its momentum. Mathematically, it is represented as FΔt = Δ(p = mv), where F is the force, Δt is the time interval, and Δ(p = mv) is the change in momentum.

  • How can you calculate the force exerted by a fluid?

    -The force exerted by a fluid can be calculated using the equation F = (ΔM/ΔT) * V, where ΔM is the mass flow rate of the fluid (kg/s), ΔT is the time interval (s), and V is the velocity of the fluid (m/s).

  • What is the conservation of momentum principle?

    -The conservation of momentum principle states that the total momentum of a system remains constant if no external forces act upon it. This means that the sum of the momentum of all objects in a system before an event is equal to the sum after the event.

  • What is the difference between an elastic and an inelastic collision?

    -In an elastic collision, both momentum and kinetic energy are conserved. In an inelastic collision, only momentum is conserved, and some kinetic energy is transformed into other forms of energy, such as heat or sound.

  • How can you find the final speed of two objects that stick together after an inelastic collision?

    -For two objects that stick together after an inelastic collision, you can use the conservation of momentum equation in the form M1 * V1 + M2 * V2 = (M1 + M2) * Vf, where Vf is the final velocity they share after the collision.

  • What is the equation for the conservation of energy in collisions?

    -The conservation of energy in collisions is given by the equation K1_initial + K2_initial = K1_final + K2_final, where Ki represents the kinetic energy of each object before the collision and Kf represents the kinetic energy after the collision.

  • How can you solve for the final speeds in a perfectly elastic collision?

    -In a perfectly elastic collision, you need to use both the conservation of momentum and the conservation of energy equations. You would set up a system of equations using the two formulas to solve for the final speeds of both objects.

  • What is a simplified equation for finding the final speeds in an elastic collision when some variables are unknown?

    -A simplified equation for an elastic collision when the final speeds are unknown is V1_initial + V1_final = V2_initial + V2_final. This equation helps you set up a system of equations with the conservation of momentum to solve for the unknown variables.

Outlines
00:00
📚 Introduction to Impulse and Momentum

This paragraph introduces the topic of impulse and momentum, emphasizing the importance of understanding key formulas for success in related exams. It begins with the fundamental concept of momentum, defined as the product of mass and velocity, and highlights the vector nature of this quantity. The paragraph also mentions the availability of example problems and practice tests for further study, encouraging viewers to check the description section for links. The focus here is on grasping the basic principles and equations, such as momentum (mass times velocity) and impulse (force times time), which are crucial for solving problems in this area of physics.

05:00
💡 Calculating Impulse and Force with Momentum

The second paragraph delves deeper into the calculation of impulse and force using the concept of momentum. It explains how impulse, the product of force and time, can be determined and how it relates to momentum. The paragraph uses the example of a water hose to illustrate how the force exerted by a fluid can be calculated using the mass flow rate and velocity. It also introduces the concept of the impulse-momentum theorem, which states that impulse is equal to the change in momentum (FΔt = Δp). Additionally, the paragraph touches on the relationship between force and the rate of change of momentum, highlighting that force can be described as the derivative of the momentum function with respect to time. This section is rich in equations and examples that help to clarify the principles discussed.

10:03
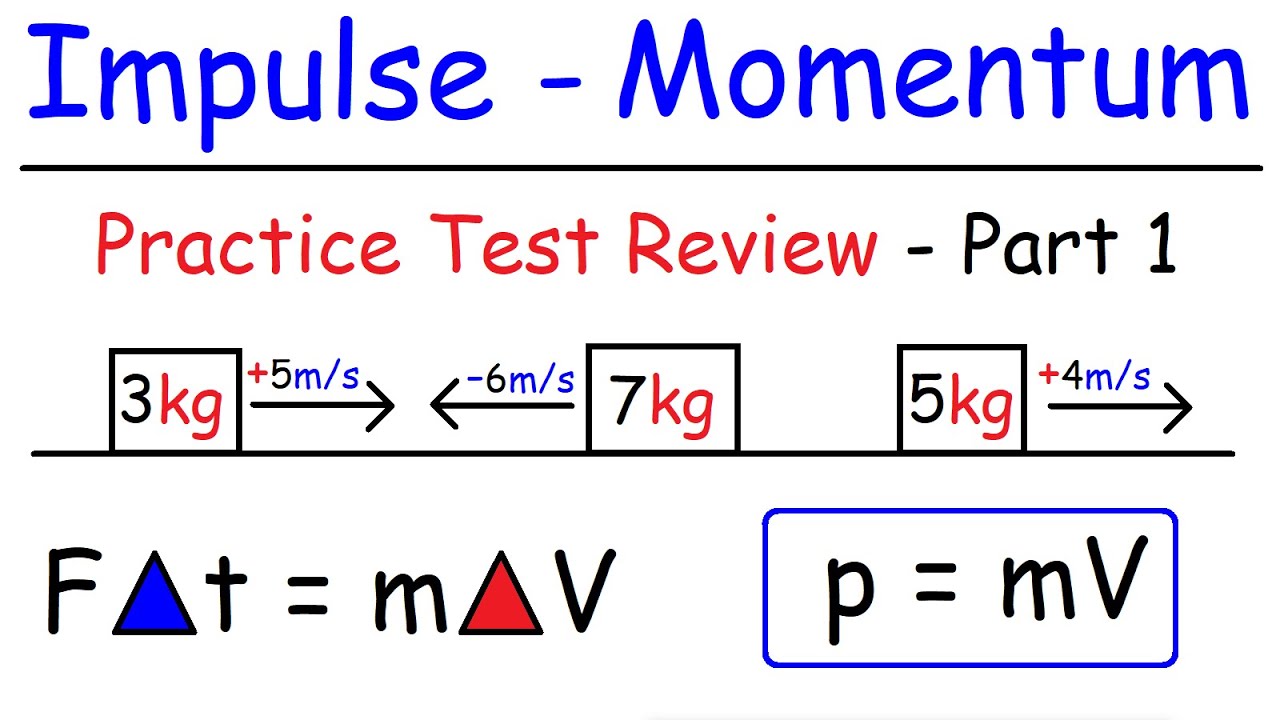
🚫 Inelastic and Elastic Collisions: Momentum Conservation

The third paragraph discusses the conservation of momentum in the context of inelastic and elastic collisions. It differentiates between the two types of collisions, noting that while momentum is conserved in both, kinetic energy is only conserved in elastic collisions. The paragraph provides a detailed explanation of how to apply the conservation of momentum formula in scenarios where objects stick together after colliding (inelastic collision) and when they bounce off each other (elastic collision). It emphasizes the importance of considering external forces and the conditions under which the conservation laws hold true. The explanation includes specific examples and equations to illustrate the calculation of final speeds after collisions, highlighting the need to solve systems of equations when certain variables are unknown.

15:06
🎓 Summary of Impulse, Momentum, and Collision Dynamics

In the final paragraph, the video script provides a summary of the main equations and concepts covered in the chapter on impulse, momentum, and collision dynamics. It reiterates the significance of understanding these principles for academic success. The paragraph briefly touches on the topics of inelastic and elastic collisions, reinforcing the principles of momentum conservation and the differences between these types of collisions. The summary serves as a recap for viewers, reinforcing the key takeaways from the video and providing a solid foundation for further study and application of the concepts discussed.

Mindmap
Keywords
💡momentum
Momentum is a fundamental concept in physics, defined as the product of an object's mass and its velocity. In the context of the video, momentum is a vector quantity, meaning it has both magnitude and direction. The script provides an example of a 10 kg block moving at 6 m/s, resulting in a momentum of 60 kg·m/s. Understanding momentum is crucial for solving problems related to motion, collisions, and impulse, as it represents the quantity of motion an object possesses.
💡vector
A vector is a mathematical representation of a physical quantity that has both magnitude and direction. In the video, the concept of vectors is introduced to explain how momentum, which is a vector, is different from a scalar like mass, which only has magnitude. The script uses the example of a block's momentum to illustrate that vectors have directionality, which is essential when dealing with problems of motion and forces in physics.
💡impulse
Impulse is the product of force and the time over which it acts, and it is a measure of the change in momentum of an object. In the video, impulse is described as the effect of applying a force to an object over a specific time period, such as a force of 100 Newtons applied for 8 seconds resulting in an impulse of 800 Newton·seconds. Impulse is a key concept in understanding how forces can change an object's state of motion.
💡force
Force is a physical quantity that can cause an object to change its state of motion or shape. In the video, force is used in the context of calculating impulse and is also related to mass and acceleration through Newton's Second Law. The script explains that force, when combined with time, can result in an impulse that changes the momentum of an object, such as pushing a block across a floor.
💡Newton's Second Law
Newton's Second Law of Motion states that the force acting on an object is equal to the mass of the object multiplied by its acceleration. In the video, this law is used to derive the relationship between impulse and momentum, as well as to explain how forces can lead to changes in velocity and, consequently, momentum. The script also adjusts this law to incorporate mass flow rates and fluid dynamics, demonstrating its versatility in solving different types of physics problems.
💡mass flow rate
The mass flow rate refers to the amount of mass of a fluid that passes through a given area per unit of time. In the video, the concept is used to calculate the force exerted by a fluid, such as water coming out of a hose, on an object. The script provides an example where water exits the hose at a speed of 20 m/s and a mass flow rate of 5 kg/s, resulting in a force of 100 Newtons being exerted on a block.
💡collision
A collision occurs when two or more objects come into contact with each other, often resulting in a transfer or redistribution of momentum and energy. The video discusses two types of collisions: inelastic and elastic. In an inelastic collision, momentum is conserved but kinetic energy is not, as seen when two blocks stick together after colliding. In an elastic collision, both momentum and kinetic energy are conserved, as would be the case if the blocks bounced off each other after the collision.
💡conservation of momentum
The principle of conservation of momentum states that the total momentum of a closed system remains constant if no external forces act upon it. In the video, this principle is used to solve problems involving collisions, where the total momentum before the collision is equal to the total momentum after the collision. The script emphasizes the importance of this principle in understanding changes in velocity and direction of objects during collisions.
💡kinetic energy
Kinetic energy is the energy that an object possesses due to its motion. In the context of the video, it is discussed in relation to collisions, where it is either conserved or not depending on whether the collision is elastic or inelastic. The script explains that in an elastic collision, both momentum and kinetic energy are conserved, whereas in an inelastic collision, only momentum is conserved.
💡elastic collision
An elastic collision is a type of collision in which both momentum and kinetic energy are conserved. In the video, the script describes a scenario where two balls bounce off each other after a collision, and it is emphasized that this type of collision is perfectly elastic, meaning that the total kinetic energy before the collision is equal to the total kinetic energy after the collision.
💡inelastic collision
An inelastic collision is a collision where momentum is conserved, but kinetic energy is not. In the video, this is illustrated by two blocks sticking together after a collision; they move with the same final speed, but some of the initial kinetic energy is transformed into other forms of energy, such as heat or sound, hence not conserved.
Highlights

Momentum is mass times velocity, represented as a vector quantity.

For a 10 kg block moving at 6 m/s, the momentum is 60 kg·m/s, demonstrating the calculation of momentum.

Impulse is calculated as the product of force and time, denoted by F∆t.

An impulse of 800 N·s could result from 100 N applied for 8 seconds or 1000 N applied for 0.8 seconds.

Impulse is equal to the change in momentum, derived from Newton's Second Law and the definition of acceleration.

The impulse-momentum theorem states that F∆t = ∆(p = mv), a key equation for solving problems involving impulse and momentum.

Force can be calculated using the mass flow rate and velocity for a fluid, as shown in the water hose example.

The equation F = (∆m/∆t) * v is used to determine the force exerted by a fluid on an object.

Force is the derivative of the momentum function with respect to time, providing an alternative way to calculate force.

In an inelastic collision, momentum is conserved, but kinetic energy is not, unlike in an elastic collision where both are conserved.

The conservation of momentum formula states that the total momentum before collision equals the total momentum after collision in a closed system with no external forces.

For objects sticking together after collision, the simplified equation M1*V1 + M2*V2 = (M1 + M2)*Vf is used to find the final speed.

In an elastic collision, the conservation of momentum and energy must be considered, using both momentum and energy equations to solve for final speeds.

When dealing with an elastic collision and missing final speeds, a system of equations using both momentum and energy conservation must be set up for solution.

The video provides example problems and a practice test for further understanding of impulse, momentum, and collision principles.

Transcripts

Browse More Related Video

AP Physics C: Momentum, Impulse, Collisions & Center of Mass Review (Mechanics)

Collisions: Crash Course Physics #10

AP Physics 1 review of Momentum and Impulse | Physics | Khan Academy

Impulse and Momentum Conservation - Inelastic & Elastic Collisions

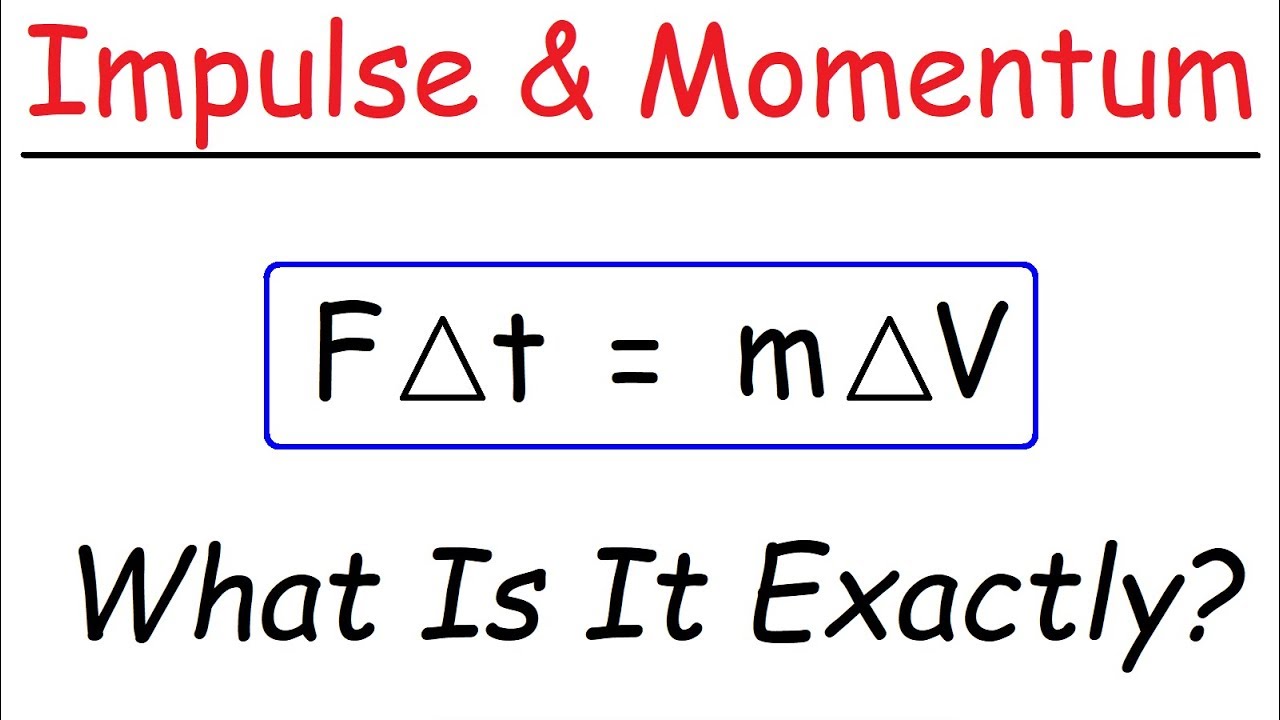
Introduction to Impulse & Momentum - Physics

2022 Live Review 5 | AP Physics 1 | Understanding Impulse and Momentum

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEducationImpulseMomentumExamPreparationForceCalculationCollisionAnalysisMassVelocityEnergyConservationFluidDynamicsInelasticCollisionElasticCollision