Introduction to Impulse & Momentum - Physics

The Organic Chemistry Tutor
28 Oct 201812:19
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video delves into the concepts of impulse and momentum, starting with momentum defined as mass times velocity, illustrating its vector nature with direction. It uses examples to explain how momentum is calculated and its units. The video then introduces impulse as force multiplied by time and relates it to momentum via the impulse-momentum theorem. It also explores the connection between force, momentum change, and Newton's second law, culminating in an example problem that demonstrates calculating impulse, change in momentum, and final velocity of an object.

Takeaways
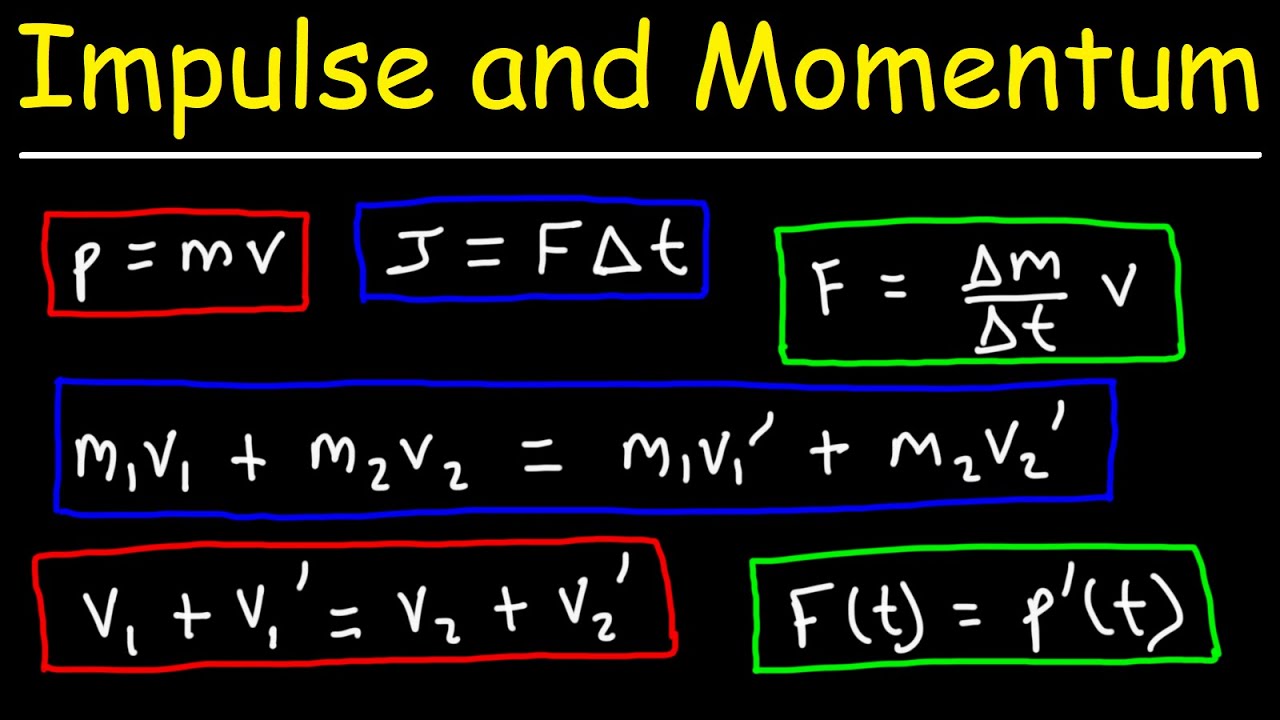
  • 🚂 Momentum is the product of mass and velocity, symbolized by p, and is essentially mass in motion.
  • 🏎️ Both heavy objects moving slowly and lighter objects moving fast can have significant momentum.
  • 🔄 Momentum is a vector quantity, meaning it has both magnitude and direction.
  • ⚖️ The units for momentum are kilograms times meters per second (kg·m/s).
  • 📏 Momentum is positive when an object moves to the right and negative when it moves to the left.
  • ⏲️ Impulse is the product of force and time, represented by I, and has the units newtons times seconds (N·s).
  • 🔁 According to the impulse-momentum theorem, impulse equals the change in momentum of an object.
  • 📉 Force can be defined as the rate of change of momentum, aligning with Newton's second law.
  • 📐 Example calculations illustrate how to determine impulse, change in momentum, final momentum, and final velocity using given values for mass, velocity, and force.
  • 📚 The video emphasizes the importance of understanding the direction of force and velocity vectors in determining the sign (positive or negative) of momentum and impulse.
Q & A

  • What is the definition of momentum in physics?

    -Momentum, represented by the lowercase symbol 'p', is the product of an object's mass and its velocity. It is essentially mass in motion, meaning any object that is moving has momentum.

  • Is momentum a scalar or a vector quantity?

    -Momentum is a vector quantity. This is because it results from multiplying a scalar (mass) by a vector (velocity), and the product retains the directionality of the vector component.

  • What are the units of momentum in physics?

    -The units of momentum are kilograms times meters per second (kg·m/s), which reflects the combination of mass in kilograms and velocity in meters per second.

  • How do you calculate the momentum of a 10 kg block sliding at 5 m/s east on a frictionless surface?

    -The momentum of the block is calculated by multiplying its mass (10 kg) by its velocity (5 m/s east). The result is a momentum of 50 kg·m/s to the east.

  • If an object is moving to the left, should the momentum be positive or negative?

    -If an object is moving to the left, the momentum should be negative, as it indicates motion in the negative x-direction.

  • What is impulse in physics?

    -Impulse in physics is the product of force and the time over which the force is applied, and it is represented by the letter 'i' in this context.

  • What are the units for impulse?

    -The units for impulse are newtons times seconds (N·s), derived from the unit of force (newtons) and time (seconds).

  • According to the impulse-momentum theorem, how is impulse related to an object's momentum?

    -The impulse-momentum theorem states that the impulse applied to an object is equal to the change in the object's momentum.

  • How can you define force in terms of momentum?

    -Force can be defined as the rate at which the momentum of an object changes, mathematically expressed as the change in momentum (Δp) over the change in time (Δt), or Δp/Δt.

  • In the context of Newton's second law, how is force related to mass, acceleration, and momentum?

    -According to Newton's second law, the net force acting on an object is equal to the mass of the object times its acceleration (F = ma). This is related to momentum as force is the rate of change of momentum over time.

  • Given a block with a mass of 50 kg and an applied force of 200 N for 5 seconds, how do you calculate the final velocity and momentum of the block if it was initially moving at 10 m/s east?

    -First, calculate the impulse (200 N * 5 s = 1000 N·s). Then, use the impulse-momentum theorem to find the change in momentum (Δp = 1000 kg·m/s). Divide this by the mass to find the change in velocity (Δv = 20 m/s). Add the initial velocity to get the final velocity (v_final = 10 m/s + 20 m/s = 30 m/s). Finally, calculate the final momentum (p_final = mass * final velocity = 50 kg * 30 m/s = 1500 kg·m/s).

Outlines
00:00
🚀 Understanding Momentum and Its Properties

This paragraph introduces the concept of momentum, defining it as the product of mass and velocity, symbolized by the lowercase 'p'. It emphasizes that any moving object possesses momentum, with mass and speed being the key factors. The paragraph also clarifies that momentum is a vector quantity, inheriting both magnitude and direction from velocity, and explains the standard units for measuring momentum as kilograms times meters per second. An example calculation is provided to illustrate how to determine the momentum of an object moving in a specific direction, highlighting the importance of considering the direction of motion when calculating momentum.

05:01
🔍 Exploring Impulse and the Impulse-Momentum Theorem

The second paragraph delves into the concept of impulse, defined as the product of force and time, with the unit being newtons times seconds. It introduces the Impulse-Momentum Theorem, which states that the impulse applied to an object is equal to the change in the object's momentum. The paragraph further explains that impulse and momentum, though measured in different units, are fundamentally equivalent. It also explores the relationship between force, impulse, and momentum, revealing that force can be understood as the rate of change of momentum over time. An example is provided to calculate the impulse acting on an object and to determine the change in momentum, with a focus on the directionality of the force and its effect on momentum.

10:03
📚 Applying Impulse and Momentum in a Practical Scenario

The final paragraph presents a practical example problem involving a block on a frictionless surface subjected to a force over a specific time period. It guides the viewer through calculating the impulse exerted on the block, the change in momentum, and the final momentum and velocity of the block. The explanation ties together concepts from the previous paragraphs, such as the relationship between force, acceleration, and the rate of change of momentum. The example serves to reinforce the understanding of how impulse and momentum interact in real-world situations, concluding the video with a comprehensive application of the discussed principles.

Mindmap
Keywords
💡Momentum
Momentum is a fundamental concept in physics, representing the product of an object's mass and its velocity. It is a vector quantity, meaning it has both magnitude and direction. In the video, momentum is introduced as 'mass in motion,' emphasizing its importance in describing the motion of objects like a train or a sports car. The formula for momentum is presented as 'mass times velocity,' and its units are kilograms times meters per second, as illustrated with the example of a 10-kilogram block sliding at 5 meters per second east.
💡Scalar Quantity
A scalar quantity is a physical quantity that is fully described by a magnitude alone, without any direction. In the context of the video, mass is identified as a scalar quantity because it does not have a directional component. The video explains how multiplying a scalar by a vector, such as mass times velocity, results in a vector, which in the case of momentum, acquires direction from the velocity component.
💡Vector Quantity
A vector quantity is a physical quantity that has both magnitude and direction. The video clarifies that velocity is a vector quantity, as it specifies not just how fast an object is moving but also the direction of its motion. This is contrasted with mass, which is a scalar, and the resulting momentum is a vector because it inherits the direction from velocity.
💡Impulse
Impulse in physics is defined as the product of force and the time over which the force is applied. It is a measure of the change in momentum of an object when a force acts on it for a certain period. The video introduces impulse with the formula 'force multiplied by time' and explains its units as newtons times seconds, which are equivalent to the units of momentum.
💡Impulse-Momentum Theorem
The Impulse-Momentum Theorem is a principle in physics that states the impulse applied to an object is equal to the change in the object's momentum. The video uses this theorem to explain the relationship between force, time, and the resulting change in an object's momentum, highlighting that a force acting on an object over a time interval results in a change in the object's velocity.
💡Force
Force is a vector quantity that describes the interaction causing a change in the motion of an object. The video defines force as the rate at which the momentum of an object changes, expressed as delta p over delta t. It is related to the concept of acceleration, as per Newton's second law, where the net force on an object is equal to the mass of the object times its acceleration.
💡Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. In the video, acceleration is used to relate the change in velocity to the force applied, as per Newton's second law. It is exemplified in the context of calculating the final velocity of an object when a known force is applied over a certain time period.
💡Newton's Second Law
Newton's second law of motion states that the net force acting on an object is equal to the product of the object's mass and its acceleration. The video connects this law to the concept of impulse, explaining that the force can be understood as the rate of change of momentum, which is directly related to mass and acceleration.
💡Units of Measurement
Units of measurement are used to express the magnitude of physical quantities. The video discusses the units for momentum (kilograms times meters per second) and impulse (newtons times seconds), emphasizing their equivalence and the importance of understanding these units in the context of physical calculations.
💡Direction
Direction is a property of vector quantities that specifies the orientation of the quantity in space. The video explains how the direction of an object's motion affects the sign of its momentum, with positive momentum indicating motion to the right and negative momentum indicating motion to the left.
💡Example Problem
An example problem is a practical illustration used to demonstrate how to apply theoretical concepts to a specific scenario. The video uses an example problem involving a block with a given mass and velocity to calculate momentum, and another involving a force applied over time to calculate impulse and the resulting change in momentum and velocity.
Highlights

Momentum is defined as mass times velocity, representing mass in motion.

Momentum is a vector quantity, having both magnitude and direction.

The unit of momentum is kilograms times meters per second.

A 10 kg block sliding at 5 m/s east has a momentum of 50 kg*m/s to the right.

A 20 kg object moving at 3 m/s west has a momentum of -60 kg*m/s, indicating leftward movement.

Impulse is the product of force and time, measured in newtons times seconds.

Impulse-momentum theorem states impulse equals change in an object's momentum.

Impulse and momentum have equivalent units, though typically represented differently.

Force can be defined as the rate of change of momentum (Δp/Δt).

Newton's second law relates force, mass, and acceleration (F = ma).

Example problem: Calculating impulse on a 50 kg block with a 200 N force over 5 seconds.

Impulse determines whether the force increases or decreases an object's momentum.

Calculating final momentum involves mass, initial velocity, and change in velocity.

The final velocity of an object can be found by adding the change in velocity to the initial velocity.

The video provides additional resources on impulse, momentum, and collision problems.

The video concludes with a summary of the relationship between impulse and momentum.

Transcripts

Browse More Related Video

What Are Momentum and Impulse? | Physics in Motion

IGCSE Physics [Syllabus 1.6] Momentum

College Physics 1: Lecture 26 - Impulse and Momentum

High School Physics - Momentum & Impulse

Angular momentum | Moments, torque, and angular momentum | Physics | Khan Academy

Impulse and Momentum - Formulas and Equations - College Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ImpulseMomentumPhysicsTheoremForceVelocityMassMotionEducationalTutorial