AP Physics C: Momentum, Impulse, Collisions & Center of Mass Review (Mechanics)

Flipping Physics
2 Apr 201711:40
EducationalLearning
32 Likes 10 Comments

TLDRThis video script from Flipping Physics offers a comprehensive review of key concepts in AP Physics C Mechanics, focusing on momentum, impulse, collisions, and center of mass. It clarifies that momentum (mass times velocity) and impulse (force times time) are vectors with units of kilogram meters per second, and are conserved in all collisions. The script differentiates between elastic and inelastic collisions, emphasizing that kinetic energy is conserved only in the former. It also explains the calculation of the center of mass for both particle systems and rigid objects, highlighting the importance of understanding mass distribution. Although some equations discussed, such as those for volumetric mass density, are not on the AP equation sheet, they are instrumental for grasping the principles behind center of mass calculations.

Takeaways
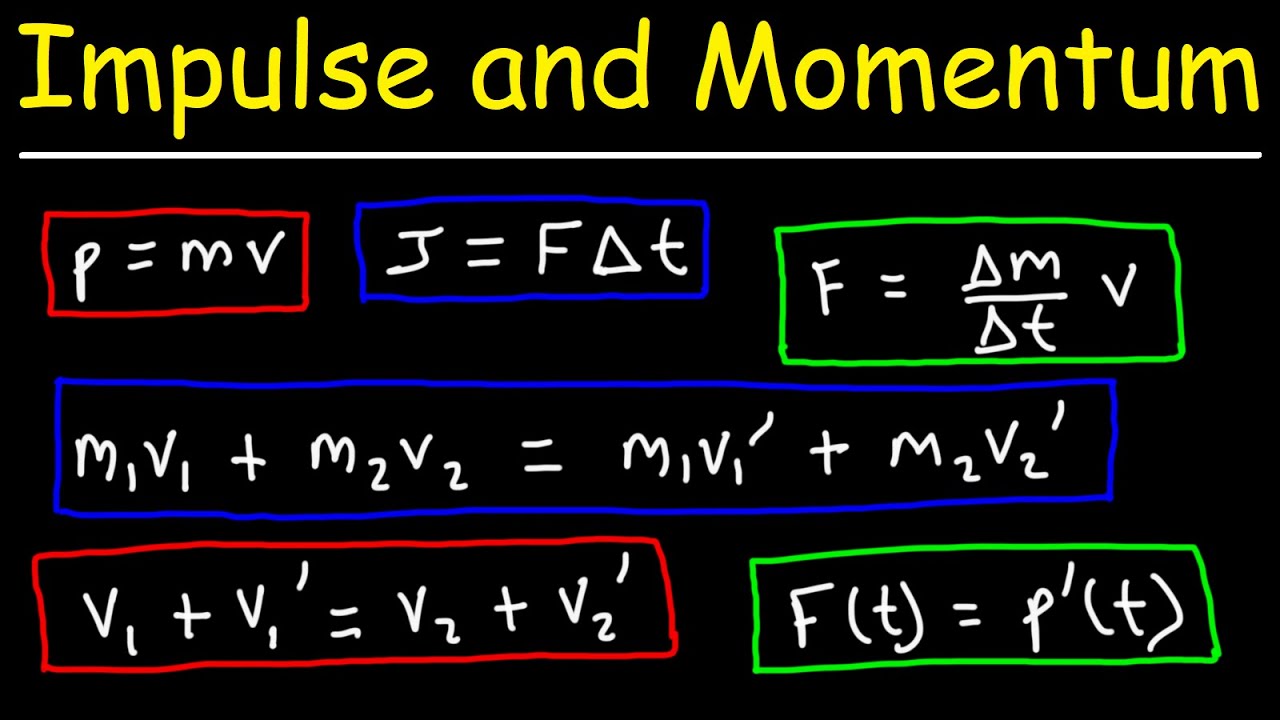
  • 📊 Momentum is defined as mass times velocity and is a vector with units of kilograms meters per second.
  • 📝 Newton's second law in terms of momentum states that the net force on an object is equal to the derivative of its momentum with respect to time.
  • 🔍 The product rule applied to Newton's second law assumes the mass of the object is constant for the net force to equal mass times acceleration.
  • ⚖️ Conservation of momentum applies when all forces are internal to a system, meaning the system's momentum remains constant over time.
  • 💥 Momentum is conserved in all collisions and explosions due to internal forces within the system.
  • 🔄 Impulse, or the change in momentum, is defined as the integral of net force with respect to time and has units of Newton's seconds.
  • ⚡ The impulse approximation assumes the force of impact during a collision overshadows other forces, allowing it to be approximated as the net force.
  • 💡 Elastic collisions conserve kinetic energy, while inelastic collisions do not. Perfectly inelastic collisions result in objects sticking together post-collision.
  • 📌 The center of mass of a system is calculated by the weighted average of the positions of all particles, with respect to their masses.
  • 🔧 The position, velocity, and acceleration of the center of mass can be determined, though only the position equation is on the AP equation sheet.
Q & A

  • What is the equation for momentum?

    -Momentum is calculated as the product of an object's mass and its velocity, represented as p = mv, where 'p' is momentum, 'm' is mass, and 'v' is velocity.

  • How do you differentiate between momentum (lower-case p) and power (upper-case P)?

    -Momentum (lower-case p) is a vector quantity that represents the product of an object's mass and velocity. Power (upper-case P), on the other hand, is the rate at which work is done or energy is transferred over time and is not directly related to momentum.

  • What are the units for momentum?

    -The units for momentum are kilograms meters per second (kg·m/s). There is no special name for these units; they are simply expressed as kilogram meters per second.

  • Can you explain Newton's second law in terms of momentum?

    -Newton's second law in terms of momentum states that the sum of the forces acting on an object or system of objects is equal to the rate of change of momentum with respect to time. Mathematically, this is expressed as F_net = d(mv)/dt.

  • What is the assumption made when using the equation F_net = ma (Newton's second law)?

    -The equation F_net = ma assumes that the mass of the object is constant over time, which implies that the derivative of mass with respect to time is zero.

  • Under what conditions can we apply the conservation of momentum?

    -The conservation of momentum can be applied when all the forces acting on a system are internal, meaning there are no external forces acting on the system, or the sum of external forces is zero.

  • How is impulse related to momentum, and what is its symbol?

    -Impulse is the change in momentum of an object and is represented by a capital letter 'J'. It is calculated as the integral of the net force acting on an object over the time interval during which the force is applied.

  • What are the units for impulse, and how do they compare to the units for momentum?

    -The units for impulse are Newton seconds (N·s), which are equivalent to the units for momentum, kilogram meters per second (kg·m/s), since impulse is force times time.

  • What is the impulse approximation, and when is it used?

    -The impulse approximation is used when the force of impact during a collision is so large that it overshadows all other forces, allowing us to approximate the net force as being equal to the force of impact during the collision. This is typically true for large impact forces that occur over a short time interval.

  • What is the difference between elastic and inelastic collisions in terms of momentum and kinetic energy conservation?

    -Both elastic and inelastic collisions conserve momentum. The difference lies in the conservation of kinetic energy. In elastic collisions, kinetic energy is conserved, while in inelastic collisions, some kinetic energy is not conserved and is often converted into other forms of energy, such as heat or sound.

  • Can you describe the concept of center of mass and its importance in physics?

    -The center of mass of a system of particles is the point at which the system's mass is considered to be concentrated. It is calculated as the sum of the products of each particle's mass and its position vector, divided by the total mass of the system. The center of mass is important because it is the point that moves with a constant velocity when no external forces are acting on the system.

  • How do you calculate the position of the center of mass for a rigid object with a specific shape?

    -For a rigid object with a specific shape, the position of the center of mass is calculated by taking the integral with respect to mass of the location of all infinitesimally small pieces of the object (dm) relative to a zero reference line, and then dividing by the total mass of the object.

  • What are the different types of mass densities, and how are they used in physics?

    -There are three types of mass densities: volumetric mass density (rho), which is mass per unit volume; surface mass density (sigma), which is mass per unit area; and linear mass density (lambda), which is mass per unit length. These densities are helpful when determining the center of mass of rigid objects with shape, especially in problems involving non-uniform density distributions.

Outlines
00:00
📚 AP Physics C Mechanics Review

This paragraph introduces a review session on key concepts of AP Physics C Mechanics, focusing on momentum, impulse, collisions, and center of mass. It clarifies the equation for momentum (mass times velocity), noting that momentum and velocity are vectors with units of kilogram meters per second. The conversation explains Newton's second law in terms of momentum, highlighting that it assumes constant mass and introduces the concept of conservation of momentum for systems with only internal forces. The impulse-momentum theorem is derived, defining impulse as the integral of net force over time, with units of Newton seconds, equivalent to kilogram meters per second. The impulse approximation is also introduced, simplifying the impact force during a collision as the dominant force.

05:03
🚀 Understanding Collisions and Center of Mass

The second paragraph delves into the types of collisions, distinguishing between elastic (where kinetic energy is conserved) and inelastic collisions (where it is not). Perfectly inelastic collisions, where objects stick together after impact, are also discussed. The paragraph then explains the concept of center of mass, providing formulas for calculating its position, velocity, and acceleration in a system of particles. It emphasizes that only the position equation is on the AP exam, and introduces the integral method for finding the center of mass in rigid objects with shape, although it notes that this specific integral is not provided on the AP equation sheet.

10:05
📘 Advanced Concepts in Physics C Mechanics

The final paragraph covers additional concepts not included on the AP Physics C Mechanics equation sheet, such as volumetric mass density (represented by rho), surface mass density (represented by sigma), and linear mass density (represented by lambda). While these densities are helpful for determining the center of mass in rigid objects, the paragraph humorously acknowledges that they are not provided on the exam's equation sheet. The review concludes with an invitation to explore rotational kinematics or visit the AP Physics C review webpage, thanking the audience for their engagement in the learning process.

Mindmap
Keywords
💡momentum
Momentum is a fundamental concept in physics that describes the quantity of motion of an object. It is defined as the product of an object's mass and its velocity, and is represented mathematically as 'momentum = mass × velocity'. In the context of the video, momentum is a vector quantity, meaning it has both magnitude and direction, and its units are kilograms meters per second (kg·m/s). The script emphasizes the distinction between momentum (lower-case 'p') and power (upper-case 'P'). Momentum is central to the theme of the video as it is used to derive other important concepts such as impulse and is key in understanding collisions and the conservation of momentum.
💡Newton's second law
Newton's second law of motion relates the force exerted on an object to its change in momentum. In terms of momentum, the law states that the sum of the forces acting on an object is equal to the rate of change of the object's momentum with respect to time, mathematically expressed as 'F = dp/dt'. The video script clarifies that force and momentum are vectors, and by using the product rule, the law can be expanded to 'net force = (d(mv)/dt)', which simplifies to 'net force = mass × acceleration' when the mass is constant. This law is integral to the video's theme as it connects force, mass, velocity, and acceleration, and sets the stage for discussing the conservation of momentum.
💡conservation of momentum
The principle of conservation of momentum states that if no external forces act on a system, the total momentum of the system remains constant. The script explains that this principle is applicable when all forces are internal to the system, meaning the sum of external forces is zero, leading to no change in the system's momentum over time. This concept is crucial in the video as it is used to analyze collisions and explosions, where the total momentum before and after the event remains the same, assuming an isolated system.
💡impulse
Impulse is defined as the integral of force with respect to time and is often introduced through the impulse-momentum theorem. The video script describes impulse as the product of force and the time interval over which the force is applied, mathematically represented as 'J = ∫F dt'. Impulse is a vector quantity, and its units are newton-seconds (N·s), which are equivalent to the units of momentum (kg·m/s). The script also differentiates impulse from work, which is the integral of force with respect to position, not time. Impulse is central to the video's narrative as it helps explain the effects of forces over time, particularly in collisions.
💡collisions
In the context of the video, collisions are events where two or more objects interact with each other through forces. The script distinguishes between elastic and inelastic collisions based on whether kinetic energy is conserved. Elastic collisions are those where both momentum and kinetic energy are conserved, while inelastic collisions are those where kinetic energy is not conserved, often converting into other forms of energy like heat and sound. Perfectly inelastic collisions, a subset of inelastic collisions, result in the objects sticking together after the collision. Understanding collisions is essential to the video's theme as it demonstrates the application of momentum conservation and impulse.
💡center of mass
The center of mass is the point at which the mass of an object or system of objects can be considered to be concentrated for the purpose of analyzing motion. The video script explains that the position of the center of mass for a system of particles is calculated by summing the products of each particle's mass and its position, divided by the total mass of the system. The script also discusses how to find the center of mass for a rigid object with shape by integrating over the mass distribution of the object. The concept of the center of mass is important in the video as it relates to the motion and stability of objects and systems under various forces.
💡elastic collision
An elastic collision is a type of collision where both momentum and kinetic energy are conserved. The video script mentions that in elastic collisions, the total kinetic energy before the collision is equal to the total kinetic energy after the collision. This type of collision is often idealized in physics problems and is exemplified by collisions between perfectly rigid, non-deformable objects, such as billiard balls on a frictionless table.
💡inelastic collision
An inelastic collision is characterized by the non-conservation of kinetic energy, although momentum is still conserved. The video script explains that some of the initial kinetic energy is transformed into other forms of energy, such as heat and sound, during the collision. In real-world scenarios, most collisions are inelastic to some degree because perfectly elastic collisions are rare.
💡perfectly inelastic collision
A perfectly inelastic collision, also referred to as a completely or totally inelastic collision in the script, is a special case of an inelastic collision where the two objects involved stick together after the collision. This results in the maximum loss of kinetic energy and the lowest possible final velocity for the combined mass. The script uses this term to illustrate an extreme case of energy non-conservation in collisions.
💡volumetric mass density
Volumetric mass density, symbolized by the Greek letter rho (ρ) in the script, is a measure of mass per unit volume. It is defined as the total mass of an object divided by its volume. Although not on the AP Physics C equation sheet, as mentioned in the script, this concept is helpful in determining the center of mass of rigid objects with shape, particularly when integrated over the volume of the object.
💡linear mass density
Linear mass density, represented by the Greek letter lambda (λ) in the script, is the mass per unit length of an object. It is calculated by dividing the object's mass by its length. Similar to volumetric mass density, linear mass density is not on the AP Physics C equation sheet but is useful for calculating the center of mass of objects, especially when considering the distribution of mass along the length of an object.
Highlights

Momentum is defined as mass times velocity and is represented by a lower-case 'p'.

Momentum and velocity are both vector quantities, with units of kilogram meters per second.

Newton's second law in terms of momentum states that the sum of forces on an object equals the rate of change of momentum.

The derivative of velocity with respect to time equals acceleration, leading to F = ma when mass is constant.

Conservation of momentum is applicable when all forces are internal to the system.

Momentum is conserved during all types of collisions and explosions due to internal forces.

Impulse, represented by J, is the integral of net force over time and has units of Newton seconds, equivalent to momentum units.

Impulse is the area under the curve of net force over time, differing from work which is force over position.

The impulse approximation assumes the impact force during a collision is the dominant force.

Elastic collisions conserve both momentum and kinetic energy, while inelastic collisions do not conserve kinetic energy.

Perfectly inelastic collisions result in the objects sticking together, with no conservation of kinetic energy.

The center of mass position is calculated by summing mass times location of each particle and dividing by total mass.

The velocity and acceleration of the center of mass are derived similarly to its position, but with respective variables.

For a rigid object, the center of mass position is found by integrating location with respect to mass.

Volumetric mass density (rho), surface mass density (sigma), and linear mass density (lambda) are helpful for center of mass calculations.

The provided equations for density are not on the AP Physics C Mechanics equation sheet.

Transcripts

Browse More Related Video

Collisions: Crash Course Physics #10

AP Physics 1: Linear Momentum and Impulse Review

AP Physics 1 review of Momentum and Impulse | Physics | Khan Academy

Conservation of Linear Momentum

AP Physics 1 Momentum Review

Impulse and Momentum - Formulas and Equations - College Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MomentumImpulseCollisionsCenter of MassAP PhysicsPhysics ReviewEducational ContentMomentum ConservationImpulse ApproximationElastic InelasticPhysics Education