Introduction to the surface integral | Multivariable Calculus | Khan Academy

Khan Academy

6 May 201022:14

EducationalLearning

32 Likes 10 Comments

TLDRThe video script delves into the concept of surface integrals and their applications in understanding the area of surfaces in 3D space. It begins by discussing the partial derivatives of vector-valued functions and transitions into explaining how these concepts are used to calculate surface area. The script provides a visual and intuitive explanation of how small changes in parameters (s and t) map to points on a surface and how the cross product of these vectors can be used to find the area of infinitesimal parallelograms that approximate the surface. The video aims to demystify surface integrals by connecting them to familiar concepts in linear algebra and calculus, setting the stage for further exploration of more complex applications in future videos.

Takeaways

📌 The video discusses the concept of surface integrals and their importance in understanding the area of a surface.
📐 The transformation from a rectangular area in the st-plane to a surface in 3D is demonstrated through a vector-valued function.
🔍 The partial derivatives of a vector-valued function play a crucial role in determining the vectors tangent to the surface at various points.
🎨 The visualization of moving in the s and t directions helps to understand how small changes in parameters affect the surface.
🔄 The concept of a differential change in surface area (d sigma) is introduced as an infinitesimal parallelogram.
📈 The surface area of a parameterized surface can be approximated by summing up the areas of these infinitesimally small parallelograms.
🤔 The magnitude of the cross product of the partial derivatives with respect to s and t gives the area of the parallelogram formed by these vectors.
🧮 The calculation of surface integrals can be performed using double integrals over the parameter space, which sums up the areas of all the infinitesimal parallelograms.
🛠️ Surface integrals have practical applications in physics, despite the challenges in visualization and calculation.
📊 The video script provides a foundation for further exploration of surface integrals and their applications in various mathematical and physical problems.

Q & A

What is the main purpose of discussing the partial derivatives of vector-valued functions in the script?
-The main purpose is to provide the necessary tools to understand the concept of a surface integral.
How is the st plane transformed into a surface r in 3D space?
-The st plane is mapped into a surface r in 3D space through a vector-valued function defined over a certain range of parameters s and t.
What does the area under question in the st plane represent?
-The area under question represents the portion of the surface that gets mapped when any s and t values from the defined range are used.
How does the script visualize the transformation from the st plane to the surface r?
-The script uses a series of points on the st plane and shows how they correspond to points on the surface r in 3D space through the vector-valued function.
What is the significance of the vectors obtained by moving a small differential in the s and t directions?
-The vectors obtained by moving a small differential in the s and t directions are tangent vectors to the surface at that point and are used to approximate the surface area.
How does the magnitude of the cross product of these tangent vectors relate to the surface area?
-The magnitude of the cross product of the tangent vectors gives the area of the parallelogram formed by these vectors, which is an approximation of the surface area at that point.
What is the significance of the surface integral in the context of the script?
-The surface integral is used to calculate the total surface area by summing up the infinitesimally small areas (parallelograms) that make up the surface.
How does the script relate the concept of surface integrals to the previously learned concept of integrals?
-The script draws a parallel between approximating a curve's area with rectangles in standard integrals and approximating a surface's area with parallelograms in surface integrals.
What is the role of the function f(x, y, z) in the context of a surface integral?
-The function f(x, y, z) assigns a value to each point on the surface, and when multiplied by the area of the corresponding parallelogram, it allows for the calculation of a weighted surface integral.
How does the script suggest we can evaluate the surface integral?
-The script suggests that we can evaluate the surface integral by setting up a double integral over the region of the st plane, involving the cross product of the partial derivatives of the vector-valued function with respect to s and t, and multiplying by ds and dt.
What is the practical application of calculating surface integrals as discussed in the script?
-While not explicitly stated in the script, surface integrals have practical applications in various fields such as physics for calculating work done over a surface or in fluid dynamics for analyzing flow properties.

Outlines

00:00

📐 Introduction to Surface Integrals

This paragraph introduces the concept of surface integrals by discussing the partial derivatives of vector-valued functions. It explains the transformation from a rectangular area in the st-plane to a surface in 3D space, using a parameterized vector-valued function. The main goal is to provide the necessary tools to understand what a surface integral is and how it relates to the visualization of a 3D surface derived from a 2D parameter space.

05:02

🔍 Exploring Vector Quantities on the Surface

In this paragraph, the focus is on understanding the quantities associated with the surface by visualizing the mapping of points s, t to a specific point on the surface. It delves into the vector representation of these points and how small changes in s and t parameters result in new points on the surface. The paragraph uses vector math to explain the difference between vectors representing these points and emphasizes the importance of understanding these basics before moving on to more complex calculations.

10:03

🌐 Calculating Surface Area with Parallelograms

This paragraph discusses the method of calculating the surface area by breaking it down into infinitesimally small parallelograms. It explains how the cross product of two vectors along the s and t parameters of the surface can be used to find the area of these parallelograms. The concept of the magnitude of the cross product being equivalent to the area of the parallelogram is introduced, and the idea of summing these areas to approximate the total surface area is presented.

15:04

📝 Surface Integrals and Their Intuition

The paragraph aims to build an intuitive understanding of surface integrals by relating them to the cross product of partial derivatives. It explains that the small changes in surface area, represented by d sigma, can be calculated as the magnitude of the cross product of the partial derivatives with respect to s and t. The paragraph emphasizes the importance of visualizing these concepts, even though surface integrals can be challenging to grasp compared to other integrals.

20:04

🔢 Integrating Functions over the Surface

This paragraph extends the concept of surface integrals to include the integration of a function f(x, y, z) over the surface. It proposes imagining each small parallelogram multiplied by the value of the function at that point, and then integrating this product over the entire surface. The paragraph highlights the practical applications of this in physics and assures that, despite the complexity, the process is manageable with persistence and understanding of the underlying concepts.

Mindmap

Keywords

💡Partial Derivative

A partial derivative is a mathematical operation that calculates the derivative of a function with multiple variables while treating all other variables as constants. In the context of the video, partial derivatives are used to find the rate of change of a surface in the s and t directions, which is crucial for understanding surface integrals and calculating the surface area.

💡Surface Integral

A surface integral is a mathematical concept used to compute quantities over a surface, rather than a volume or a line. In the video, the surface integral is introduced as a tool to understand and calculate the area of a surface defined by a vector-valued function. It is the generalization of a line integral to two dimensions and is used to evaluate the accumulated effect of a function over a surface.

💡Vector-Valued Function

A vector-valued function is a function that takes one or more scalar inputs and produces a vector as output. In the context of this video, the vector-valued function r(s, t) defines a position in three-dimensional space based on the parameters s and t, which is used to map a 2D rectangle in the st-plane to a surface in 3D space.

💡Cross Product

The cross product is a vector operation on two vectors in three-dimensional space, resulting in a third vector that is perpendicular to the plane formed by the original two vectors. In the video, the cross product is used to find a vector perpendicular to the tangent vectors of the surface, which helps in calculating the surface area.

💡Surface Area

Surface area refers to the total area covered by the surface of a three-dimensional object. In the video, the concept of surface area is explored through the transformation of a 2D rectangle in the st-plane into a 3D surface and the calculation of this surface's area using surface integrals.

💡Parameterized Surface

A parameterized surface is a mathematical representation of a surface using parametric equations, where each point on the surface is specified by a set of parameters. In the video, the surface is parameterized by the function r(s, t), which maps points (s, t) in the st-plane to points on the surface in 3D space.

💡Tangent Vectors

Tangent vectors are vectors that lie in the plane of a surface at a given point and are used to describe the local geometry of the surface. In the video, the partial derivatives of the vector-valued function with respect to s and t represent the tangent vectors at each point on the surface.

💡Parallelogram

A parallelogram is a four-sided figure in which both pairs of opposite sides are parallel. In the context of the video, the surface is approximated by breaking it down into infinitesimally small parallelograms, each of which contributes to the total surface area.

💡Integration

Integration is a mathematical process that finds the accumulated value of a function over an interval or region, such as the area under a curve or, in this case, the surface area of a parameterized surface. The video discusses using a double integral to sum up the infinitesimally small areas (d sigmas) to find the total surface area.

💡Differential

In mathematics, a differential represents a small change in a function's value. In the context of the video, differentials ds and dt represent infinitesimally small changes in the parameters s and t of the vector-valued function, which are used to approximate the tangent vectors to the surface.

Highlights

Exploration of the concept of taking a partial derivative of a vector-valued function.

Introduction to the idea of a surface integral and its importance in understanding complex mathematical surfaces.

Visualization of the st plane transformation into a 3D surface, providing a geometric understanding of the mathematical concepts.

Explanation of how a rectangular area in the st plane maps to a surface, emphasizing the role of the vector-valued function r.

Discussion on the process of mapping individual points to their corresponding positions on the surface using the vector-valued function r.

Illustration of the transformation from a 2D rectangular area to a complex 3D surface, emphasizing the generality of the process.

Introduction to the concept of a differential in the s direction and its impact on the mapped point on the surface.

Explanation of the vector difference resulting from a small change in the s parameter, and its significance in understanding surface properties.

Analogous discussion on the t direction, highlighting the vector changes and their implications.

Intuitive explanation of the cross product of vectors and its relation to the area of a parallelogram, providing a foundation for understanding surface integrals.

Revelation that the magnitude of the cross product of two vectors along the s and t directions represents the area of a parallelogram on the surface.

Introduction to the notation d sigma, representing a small change in surface area, and its role in approximating the total surface area.

Explanation of the infinite sum of d sigmas as a method to calculate the total surface area, providing a practical approach to a complex concept.

Discussion on the representation of d sigma as the cross product of the partial derivatives of r with respect to s and t, deepening the understanding of surface integrals.

Introduction to the concept of multiplying each small parallelogram by a function f(x, y, z), extending the application of surface integrals.

Explanation of how to calculate the surface integral of a function f(x, y, z) over the entire surface, providing a method for practical applications.

Emphasis on the complexity and potential difficulty of visualizing and calculating surface integrals, while reassuring that they are manageable with persistence.

Transcripts

Browse More Related Video

Example of calculating a surface integral part 2 | Multivariable Calculus | Khan Academy

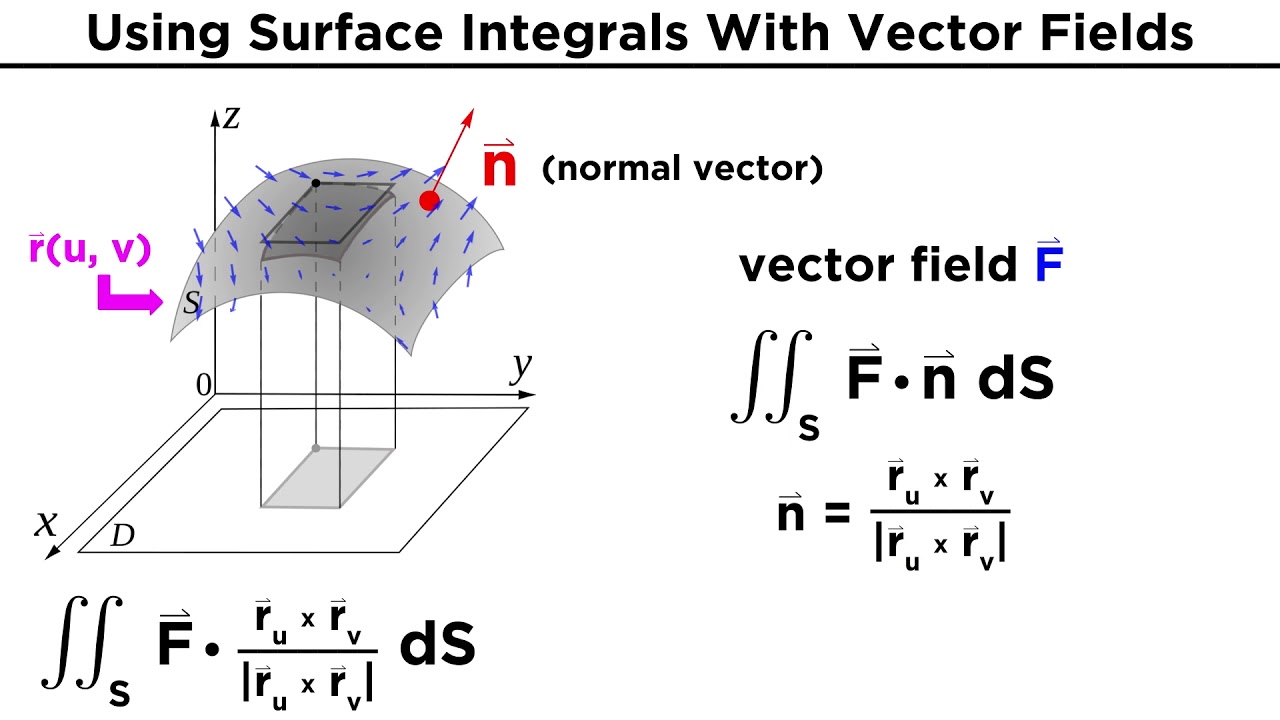
Evaluating Surface Integrals

Example of calculating a surface integral part 1 | Multivariable Calculus | Khan Academy

Constructing a unit normal vector to a surface | Multivariable Calculus | Khan Academy

Double integral 1 | Double and triple integrals | Multivariable Calculus | Khan Academy

Partial derivatives of vector-valued functions | Multivariable Calculus | Khan Academy

Related Tags

Mathematics Surface Integrals Vector Functions 3D Visualization Partial Derivatives Cross Product Area Calculation Linear Algebra Educational Content Advanced Math