Calculus 1: Concavity Examples
TLDRThis video script delves into the concept of concavity and its interpretation through the second derivative in calculus. When the second derivative is positive, a function is described as concave up, resembling an upward-facing bowl, while a negative second derivative indicates concave down, like a downward-facing bowl. Points of inflection, where concavity changes, occur where the second derivative equals zero. The script guides through finding critical numbers and classifying them as minimums or maximums using the second derivative test. It illustrates this with examples, including a parabola that is always concave up with no points of inflection, and another function that transitions from concave down to up, showcasing how to determine the nature of critical points analytically. The presenter also offers additional resources on their website for further exploration.
Takeaways
- 📚 Concavity is a concept in calculus that describes the curvature of a function's graph, with 'concave up' resembling an upward-facing bowl and 'concave down' resembling a downward-facing bowl.
- 📈 The second derivative of a function is used to determine concavity. A positive second derivative indicates the function is concave up, while a negative second derivative indicates the function is concave down.
- 🔍 Points of inflection are where the concavity of a function changes. They occur where the second derivative is zero and the concavity switches from concave up to down or vice versa.
- 📉 The first derivative of a function indicates whether the function is increasing or decreasing, but the second derivative indicates whether it is concave up or down, not the direction of increase or decrease.
- 📌 To find points of inflection, one must look for where the second derivative equals zero and there is a change in concavity from one side of the point to the other.
- 📝 The process involves first finding the first derivative of a function, setting it to zero to find critical points, and then finding the second derivative to analyze concavity.
- 📉 For a function to have points of inflection, its second derivative must be zero at some points, indicating a change in concavity.
- 📊 The second derivative test can also be used to classify critical points as minimums or maximums. If a critical point is concave up, it's a minimum, and if it's concave down, it's a maximum.
- 🔢 The second derivative test is inconclusive if the second derivative is zero at a critical point, as it does not provide information to classify the point as a minimum or maximum.
- 👨🏫 The speaker provides examples of how to compute the first and second derivatives of given functions and how to use the second derivative to determine concavity and classify critical points.
- 💻 The speaker encourages viewers to visit their website for more examples and step-by-step solutions to over 400 calculus problems.
Q & A
What is the physical interpretation of concavity in the context of a function's graph?
-The physical interpretation of concavity refers to the shape of the graph of a function. If the second derivative is positive, the function is concave up, resembling an upward-facing bowl. Conversely, if the second derivative is negative, the function is concave down, resembling a downward-facing bowl.
How does the first derivative relate to the concavity of a function?
-The first derivative indicates whether a function is increasing or decreasing by showing the sign of the slope (positive for increasing, negative for decreasing). However, it does not directly tell us about the concavity of the function, which is determined by the second derivative.
What are points of inflection on a function's graph?
-Points of inflection are the points on a graph where the concavity changes. For example, if a curve transitions from concave up to concave down or vice versa, those transition points are points of inflection.
How can you determine if a point is a point of inflection by using the second derivative?
-A point of inflection can be determined by finding where the second derivative equals zero and there is a change in concavity between the left and right of that point.
What does it mean if the second derivative of a function is always greater than zero?
-If the second derivative of a function is always greater than zero, it means that the function is concave up everywhere. This implies that the graph of the function never forms a bowl facing downward.
How can you use the second derivative to classify a critical point as a minimum or maximum?
-By using the second derivative test, if a critical point (where the first derivative is zero or undefined) is concave up, it is classified as a minimum. If it is concave down, it is classified as a maximum.
What is the second derivative of the function f(x) = x^2 - 2?
-The second derivative of the function f(x) = x^2 - 2 is simply 2, as the first derivative is 2x and its derivative is 2.
Why is the second derivative test inconclusive if the second derivative is equal to zero at a critical point?
-If the second derivative is equal to zero at a critical point, the test is inconclusive because the concavity does not change at that point, and thus it does not provide information to classify the point as a minimum or maximum.
How does the second derivative test differ from the first derivative test in determining the nature of critical points?
-The second derivative test uses the concavity of the function at critical points to determine if they are minima or maxima. In contrast, the first derivative test uses sign changes in the derivative to the left and right of the critical points.
What is the transition point in the context of the second derivative of a function?
-The transition point is where the second derivative equals zero, indicating a change in the concavity of the function. This is the point where the function transitions from being concave up to concave down or vice versa.
Outlines
📚 Understanding Concavity and Second Derivative
This paragraph delves into the concept of concavity and its interpretation through the second derivative. Concavity is described as the curvature of a function, where a positive second derivative indicates the function is 'concave up', resembling an upward-facing bowl. Conversely, a negative second derivative suggests 'concave down', akin to a downward-facing bowl. Points of inflection, where the concavity changes, are also discussed, occurring where the second derivative equals zero. The paragraph illustrates how to determine whether a function is increasing or decreasing using the first derivative, and how to identify concave up and down sections of a function using the second derivative. An example is provided with a function whose second derivative is always positive, indicating it is concave up everywhere, like an upward-facing parabola.
📉 Applying the Second Derivative Test for Critical Points
The second paragraph focuses on applying the second derivative test to find critical points in a function, which are potential minima or maxima. The process begins by finding critical numbers where the first derivative is zero. The second derivative is then used to determine the concavity at these points. If the second derivative is positive at a critical number, the function is concave up, indicating a minimum. If it is negative, the function is concave down, indicating a maximum. The test is inconclusive if the second derivative is zero. The paragraph provides step-by-step examples, including solving for critical numbers and using the second derivative to classify them as minima or maxima. It concludes with an invitation to visit the speaker's website for more calculus examples and explanations.
Mindmap
Keywords
💡Concavity
💡Second Derivative
💡Inflection Point
💡First Derivative
💡Critical Numbers
💡Minimum and Maximum
💡Sign Change
💡Parabola
💡Upward Facing
💡Second Derivative Test
Highlights
Concavity is the physical interpretation of the second derivative, indicating the shape of the curve like a bowl facing up or down.
A positive second derivative indicates the function is concave up, resembling an upward-facing bowl.
A negative second derivative suggests the function is concave down, like a bowl facing downward.
The first derivative informs about the increasing or decreasing nature of a function, while the second derivative indicates concavity.
Points of inflection are where the concavity changes, marked by a change from concave up to down or vice versa.
The second derivative equals zero at points of inflection, indicating a change in concavity.
Using the first derivative test involves looking for sign changes to determine concavity changes.
For a given function, the first derivative is computed to find critical points where the function could have minima or maxima.
The second derivative of a function can be used to determine if there are points of inflection.
If the second derivative is always positive, the function is concave up everywhere, as seen with an upward-facing parabola.
The second derivative test classifies critical numbers as minima or maxima based on concavity.
A critical number with a positive second derivative indicates a minimum, as it is concave up.
A critical number with a negative second derivative suggests a maximum, as it is concave down.
If the second derivative is zero, the test is inconclusive, and the concavity does not help classify the point.
The second derivative test provides an alternative method to the first derivative test for finding minima and maxima.
The function's concavity can be determined by analyzing the sign of the second derivative across different intervals.
The transcript provides a step-by-step guide on using the second derivative to analyze concavity and find points of inflection.
The instructor offers free access to over 400 calculus questions on their website for further examples and practice.
Transcripts
Browse More Related Video

MATH1325 Lecture 10 2 - Concavity & Points of Inflection

Concavity, Inflection Points, and Second Derivative
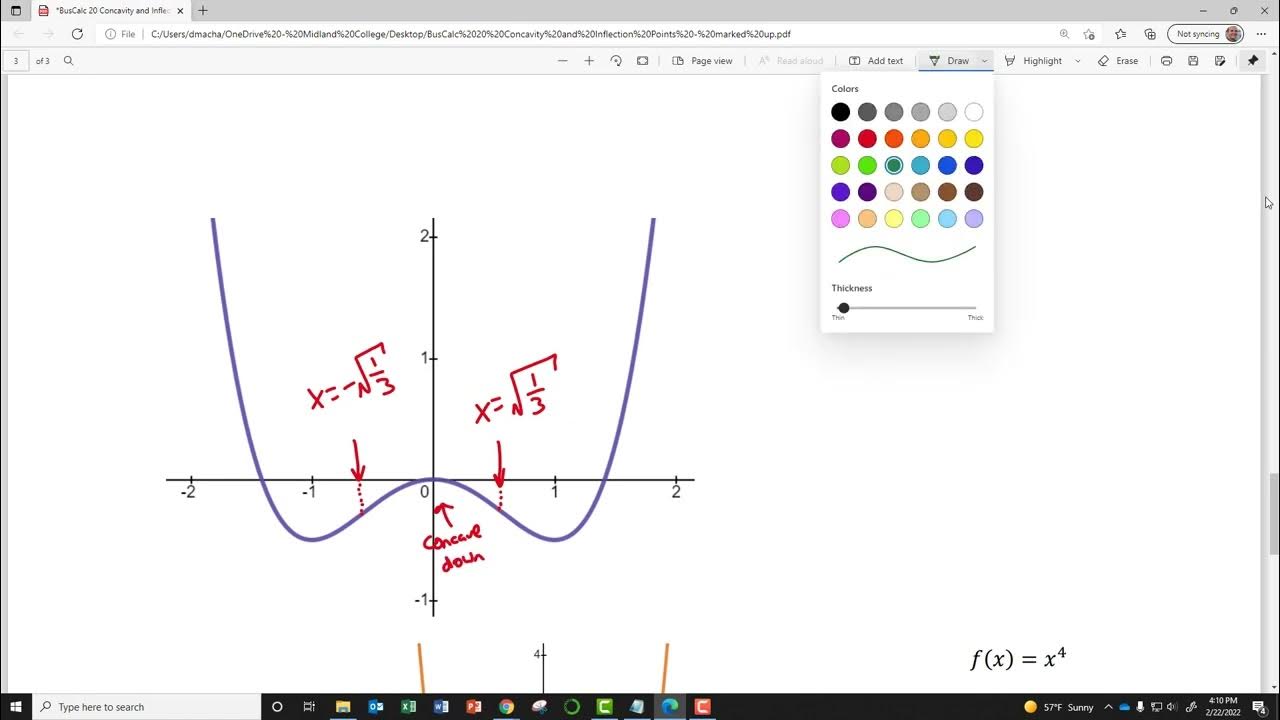
BusCalc 20 Concavity and Inflection Points

Concavity and the 2nd Derivative Test

Concavity introduction | Using derivatives to analyze functions | AP Calculus AB | Khan Academy

Finding Concavity and Inflection Points
5.0 / 5 (0 votes)
Thanks for rating: