Calculus AB/BC – 5.6 Determining Concavity of Functions over Their Domains
TLDRIn this engaging calculus lesson, Mr. Bean explains the concept of concavity and how to determine the concavity of a function over an interval. He clarifies the meaning of concave up and down using visual analogies, such as the shape of contact lenses, and then connects concavity to the behavior of the first and second derivatives of a function. Mr. Bean demonstrates that a function is concave up when its first derivative is increasing and concave down when it's decreasing, which directly relates to the sign of the second derivative. He further illustrates how to identify points of inflection, which are where the concavity changes, and emphasizes the importance of checking for sign changes in the second derivative. The lesson includes practical examples using both graphical and tabular methods, and concludes with a discussion on how the second derivative can be used to estimate the position of a tangent line relative to the function graph. This comprehensive overview is essential for understanding the shape of graphs and is a key concept for further studies in calculus.
Takeaways
- 📚 **Understanding Concavity**: Concavity refers to the curvature of a function, with 'concave up' resembling a U-shape and 'concave down' resembling an inverted U-shape.
- 🧵 **Tangent Line Analogy**: Mr. Bean uses the analogy of a rubber band to explain concavity, showing how it can stretch (concave up) or compress (concave down).
- 📈 **First Derivative and Concavity**: The sign of the first derivative (f') indicates the slope of the tangent line at a point on the function; it changes as you move along the function.
- 📉 **Second Derivative and Concavity**: If f' (the first derivative) is increasing, then f'' (the second derivative) is positive, indicating the function is concave up. Conversely, if f' is decreasing, f'' is negative, indicating concave down.
- 🔢 **Second Derivative Test**: The second derivative test states that if f'' is positive, the function is concave up, and if f'' is negative, the function is concave down.
- 🏞️ **Graph Analysis**: By analyzing the graph of a function, one can determine intervals of concavity and points of inflection where the concavity changes.
- 🔍 **Second Derivative Sign**: To determine concavity, one must check the sign of the second derivative throughout different intervals of the function's domain.
- ✍️ **Calculating Derivatives**: The process of finding the first and second derivatives of a function is essential for analyzing its concavity and identifying points of inflection.
- 🤔 **Mistakes to Avoid**: Students often mistakenly assume that a second derivative equal to zero indicates a point of inflection; however, it is the change in sign of the second derivative that confirms this.
- 📊 **Graph Interpretation**: When given a graph of the first or second derivative, one can deduce the intervals of concavity and the x-values of points of inflection by observing where the derivative crosses or touches the x-axis.
- ✅ **Tangent Line Estimation**: Knowing the concavity allows for better estimation of the function's values using tangent lines; a positive second derivative (concave up) means the tangent line will be an underestimate, while a negative second derivative (concave down) means it will be an overestimate.
Q & A
What is the definition of concavity?
-Concavity refers to the curvature of a function. A function is said to be concave up if it curves upward like the shape of a contact lens, and concave down if it curves downward.
How does the sign of the first derivative (f prime) relate to the concavity of a function?
-The sign of the first derivative (f prime) indicates the slope of the tangent line at a point on the function. If f prime is increasing, the function is concave up, and if f prime is decreasing, the function is concave down.
What does the second derivative (f double prime) signify in terms of concavity?
-The second derivative (f double prime) indicates whether the function is concave up or concave down. If the second derivative is positive, the function is concave up, and if it is negative, the function is concave down.
How can you determine the points of inflection on a graph?
-Points of inflection are determined by where the concavity of the function changes. These points occur where the second derivative changes signs, either from positive to negative or from negative to positive.
What is a common mistake students make when identifying points of inflection?
-A common mistake is assuming that wherever the second derivative equals zero, there is a point of inflection. However, a point of inflection occurs only when the second derivative changes signs, not just when it is zero.
How can you use the second derivative to determine if a tangent line to a graph is an overestimate or an underestimate at a given point?
-If the second derivative at a given point is positive, the function is concave up and the tangent line will be an underestimate of the function at points away from the tangent point. Conversely, if the second derivative is negative, the function is concave down and the tangent line will be an overestimate.
What is the significance of the second derivative in understanding the shape of a graph?
-The second derivative is crucial for understanding the shape of a graph as it provides information about the concavity of the function, which helps in determining whether the graph curves upward or downward and identifies points of inflection.
How does the sign of the second derivative affect the graph of a sinusoidal function like sine x?
-For a sinusoidal function like sine x, the sign of the second derivative determines the concavity of the graph. Positive second derivatives correspond to concave up regions, while negative second derivatives correspond to concave down regions.
What is the role of the first derivative in the context of concavity?
-The first derivative provides the slope of the tangent line at a specific point on the function. It is used to find the second derivative, which in turn is used to determine the concavity of the function.
What is the process to find the intervals of concavity for a given function?
-To find the intervals of concavity, one must first find the first and second derivatives of the function. Then, by analyzing the sign of the second derivative, one can determine whether the function is concave up or down in different intervals. Points where the second derivative is zero or undefined are potential points of inflection.
Why is it important to check the sign change of the second derivative when identifying points of inflection?
-Checking the sign change of the second derivative is important because a point of inflection is defined as a point where the concavity of the function changes. Therefore, a change in the sign of the second derivative from positive to negative or vice versa is necessary to identify a point of inflection.
How can you determine if a function is concave up or down without a graph, just using the function's equation?
-You can determine if a function is concave up or down by finding the second derivative of the function and analyzing its sign. If the second derivative is positive over an interval, the function is concave up on that interval. If the second derivative is negative, the function is concave down.
Outlines
📚 Introduction to Concavity and Its Meaning
The video begins with an introduction to the concept of concavity in calculus. Mr. Bean explains that concavity refers to the curvature of a function, which can be either concave up or concave down. He uses the analogy of a contact lens to illustrate the concept visually. The video then delves into the mathematical definition, stating that a function is concave up if its first derivative (slope of the tangent line) increases as we move along the function, and concave down if this slope decreases. The second derivative is introduced as a tool to determine concavity: a positive second derivative indicates concave up, while a negative one indicates concave down.
🔍 Analyzing Concavity with the Second Derivative
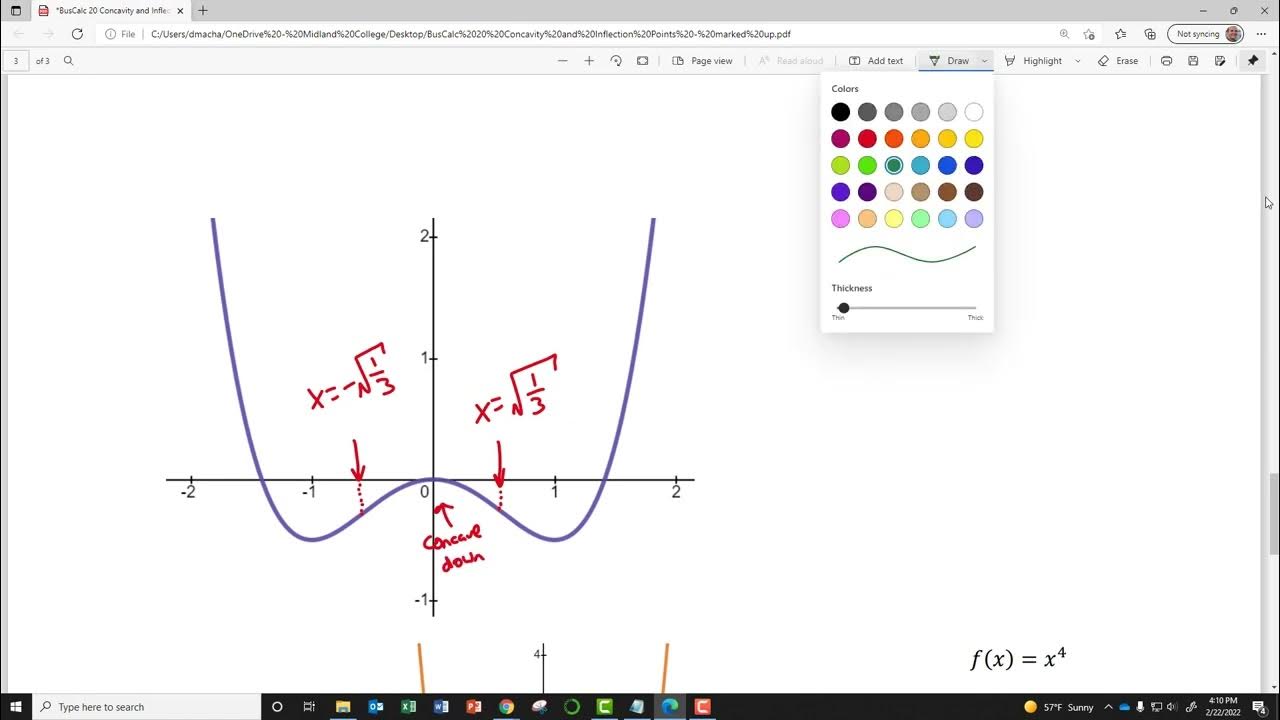
This paragraph focuses on using the second derivative to analyze the concavity of a function. The process involves setting the second derivative equal to zero to find critical points, and then using a sign chart to determine the intervals where the function is concave up or down. The video provides an example using a specific function, calculating its first and second derivatives, and then using test points to fill out the sign chart. The conclusion is that the sign of the second derivative determines the concavity, and points where the second derivative is zero or does not exist are potential points of inflection.
🤔 Common Pitfalls in Identifying Points of Inflection
The third paragraph addresses common mistakes students make when identifying points of inflection. It clarifies that a second derivative equal to zero is only a candidate for a point of inflection and the sign change must be verified. Additionally, the absence of a second derivative does not rule out the possibility of a point of inflection, as a function can still change concavity at a point where the derivative is undefined, provided the function itself is defined at that point. The video also includes a brief discussion on how to interpret graphs of the first and second derivatives to determine concavity and points of inflection.
📈 Applying Concavity to Tangent Line Estimations
In the final paragraph, the video revisits the application of concavity to estimate the function values using tangent lines. It explains that for a concave up function, the tangent line will underestimate the function value, while for a concave down function, it will overestimate. The process involves finding the first and second derivatives of a given function, evaluating the second derivative at a specific point to determine the concavity, and then deducing whether the tangent line at that point lies above or below the function. The video concludes by emphasizing the importance of understanding concavity and its applications in calculus.
Mindmap
Keywords
💡Concavity
💡First Derivative (f prime)
💡Second Derivative (f double prime)
💡Tangent Line
💡Point of Inflection
💡Product Rule
💡Chain Rule
💡Sine Function
💡Critical Points
💡Estimation
💡Graph Analysis
Highlights
Definition of concavity explained using the analogy of contact lenses
Concave up functions have increasing first derivatives, while concave down functions have decreasing first derivatives
Second derivative can determine concavity: positive implies concave up, negative implies concave down
Graphical representation of concavity using a parent sinusoid function
Procedure to find intervals of concavity using first and second derivative tests
Points of inflection occur where the second derivative changes signs
Mistaken assumption that second derivative being zero always indicates a point of inflection
Points of inflection can occur even when the second derivative does not exist, as long as the concavity changes
Interpreting f' and f'' graphs to determine concavity and points of inflection
Using concavity to estimate the position of tangent lines relative to the function graph
Example problem applying the concepts to determine if a tangent line is an overestimate or underestimate
Concavity analysis is crucial for understanding graph shapes and behavior
Clear explanation of how to identify and justify points of inflection from both graphs and derivative tables
Common mistakes to avoid when analyzing concavity and points of inflection
Practical application of concavity in fields like economics
Engaging teaching style using analogies and visual aids to clarify complex concepts
Step-by-step walkthrough of finding second derivative and using it to analyze concavity
Emphasis on the importance of checking for sign changes in the second derivative to identify points of inflection
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: