Probability: Bayes' Theorem

Mathispower4u
4 Oct 201308:25
EducationalLearning
32 Likes 10 Comments

TLDRThis lesson explores Bayes Theorem through a medical testing scenario. It demonstrates how to calculate the probability of having a virus given a positive test result, using both intuitive methods and Bayes Theorem. The example highlights the surprising low accuracy of positive tests and the importance of understanding conditional probabilities.

Takeaways
  • 🧠 Bayes Theorem is a fundamental concept in probability theory, used to find the probability of an event based on prior knowledge of conditions related to the event.
  • 🔍 The script introduces an example involving a virus and a diagnostic test to illustrate the application of conditional probability and Bayes Theorem.
  • 📉 The prevalence of the virus in the population is one in every four hundred people, which is the base rate for calculating probabilities.
  • 🌡 The diagnostic test has an 85% true positive rate and a 5% false positive rate, which are crucial for understanding the test's accuracy.
  • 📊 The script uses a table to organize information about the virus infection status and test results, facilitating the calculation of conditional probabilities.
  • 🔢 A hypothetical sample of ten thousand people is used to demonstrate the calculations, making it easier to understand the probabilities involved.
  • 🤒 The probability of having the virus (event A) is calculated as 0.025, based on the infection rate of one in four hundred.
  • 🟢 Of those infected, 85% test positive, leading to a calculation of how many in the sample would test positive given they have the virus.
  • 🟡 5% of those not infected test positive, which is the false positive rate, and this is used to calculate the number of false positives in the sample.
  • 📉 The probability of a person having the virus given a positive test result is surprisingly low at approximately 4.09%, indicating the test's limitations.
  • 📈 Conversely, the probability of not having the virus given a negative test result is high at approximately 99.6%, showing the test's reliability in ruling out the virus.
  • 📚 The script concludes by verifying the calculated probabilities using Bayes Theorem, reinforcing the theorem's validity in such calculations.
Q & A

  • What is Bayes Theorem?

    -Bayes Theorem, also known as Bayes rule or Bayes' law, is a mathematical formula that describes the probability of an event based on prior knowledge of conditions related to the event.

  • What is conditional probability?

    -Conditional probability is the probability of an event occurring given that another event has already occurred.

  • What is the significance of false positives in the context of the virus test?

    -False positives refer to the cases where a test incorrectly indicates that a person has the virus when they do not, which can lead to incorrect diagnoses and unnecessary treatment.

  • What is the probability of the virus infecting a person according to the script?

    -The script states that the virus infects one in every four hundred people, which can be represented as a probability of 0.0025.

  • How accurate is the test used to detect the virus?

    -The test is 85% accurate in detecting the virus when a person is actually infected and has a 5% false positive rate when the person does not have the virus.

  • What are the events A and B defined in the script?

    -In the script, event A is defined as the person having the virus, and event B is defined as the person testing positive for the virus.

  • How many people out of ten thousand would be expected to have the virus based on the given probability?

    -Using the probability of 0.0025, 25 out of ten thousand people would be expected to have the virus.

  • What is the probability of a person testing positive given they have the virus (P(B|A))?

    -The probability of a person testing positive given they have the virus is 85%, or 0.85.

  • What is the probability of a person testing positive but not having the virus (false positives)?

    -The probability of testing positive without having the virus is 5%, which is the false positive rate.

  • What is the calculated probability of a person actually having the virus given they tested positive (P(A|B))?

    -The calculated probability of a person having the virus given they tested positive is approximately 4.09%.

  • How does the script suggest using intuition to find conditional probabilities as opposed to memorizing Bayes Theorem?

    -The script suggests that it might often be easier to use intuition and a logical approach to determine conditional probabilities, rather than relying solely on memorizing the formula of Bayes Theorem.

Outlines
00:00
🧬 Introduction to Bayes Theorem

This paragraph introduces Bayes Theorem, a fundamental principle in probability theory. It sets the stage by discussing the concept of conditional probability using an example involving a virus test. The example involves a virus that infects one in every four hundred people and a test that is 85% accurate for detecting the virus and 5% prone to false positives. The goal is to calculate the probability of having the virus given a positive test result (P(A|B)) and the probability of not having the virus given a negative test result (P(not A|not B)). The paragraph also outlines the initial steps in setting up a table to organize the information and calculate these probabilities.

05:01
🔍 Calculating Conditional Probabilities

This paragraph delves into the calculation of conditional probabilities using the example from the previous paragraph. It explains how to use the test accuracy rates and the prevalence of the virus to determine the likelihood of a person having the virus given a positive test result. The calculations involve determining the number of people who would test positive and actually have the virus, as well as those who test positive but do not have the virus (false positives). The paragraph also discusses the calculation of the probability of not having the virus given a negative test result. The results show that only about 4.09% of people who test positive actually have the virus, indicating the test is more reliable for ruling out the virus than confirming it. The paragraph concludes by verifying these findings using Bayes Theorem, reinforcing the importance of understanding both the intuitive and mathematical approaches to probability.

Mindmap
Keywords
💡Bayes Theorem
Bayes Theorem, also known as Bayes' rule or Bayes' law, is a fundamental principle in probability theory and statistics that describes the probability of an event based on prior knowledge of conditions related to the event. In the context of the video, Bayes Theorem is used to calculate the probability of a person having a virus given that they have tested positive, which is a critical concept for understanding the accuracy of medical tests.
💡Conditional Probability
Conditional probability is the probability of an event occurring given that another event has already occurred. It is a key concept in the video, as it is used to determine the likelihood of a person having a virus based on the result of a test. The script discusses calculating the probability of having the virus given a positive test (P(A|B)) and not having the virus given a negative test (P(not A|not B)).
💡False Positives
False positives refer to the cases where a test incorrectly indicates the presence of a condition (like a virus) when it is not actually present. In the video, the script mentions that the test has a 5% false positive rate, meaning that 5% of the time, the test will incorrectly indicate that a person has the virus when they do not.
💡Probability of A given B (P(A|B))
This term represents the probability that a person has the virus given that they have tested positive. It is a central focus of the video, as it illustrates the main application of Bayes Theorem in the context of medical testing. The script calculates this probability using both intuitive methods and Bayes Theorem, highlighting its significance in understanding test accuracy.
💡Probability of not A given not B (P(not A|not B))
This concept is used to determine the probability that a person does not have the virus given that they have tested negative. It is important for understanding the reliability of a test in ruling out the presence of a virus. The script calculates this probability to demonstrate the test's effectiveness in identifying those who are virus-free.
💡Virus Infection Rate
The virus infection rate is the proportion of the population that is infected with a virus. In the video, it is stated that the virus infects one in every four hundred people, which is used to calculate the baseline probability of having the virus (P(A)) in the sample population.
💡Test Sensitivity
Test sensitivity refers to the ability of a test to correctly identify those who have a condition. In the script, it is mentioned that the test is positive 85% of the time if a person has the virus, which is the test's sensitivity. This metric is crucial for evaluating how well the test detects the virus in infected individuals.
💡Test Specificity
Test specificity is the ability of a test to correctly identify those who do not have a condition. The script discusses that 5% of the time, the test will be positive even if the person does not have the virus, which is the test's false positive rate and inversely related to specificity. High specificity is desirable to minimize false positives.
💡Sample Population
The sample population is the group of individuals from which data is collected for analysis. In the video, the script uses a sample of ten thousand people to illustrate the calculations involved in determining the probabilities related to the virus test. This sample size is used to demonstrate the application of probabilities in a practical scenario.
💡Intuitive Calculation
Intuitive calculation refers to the process of estimating probabilities or outcomes based on common sense or general understanding, without necessarily using formal mathematical methods. The script initially uses intuitive calculations to estimate the number of people who would test positive or negative for the virus, before applying Bayes Theorem for a more precise calculation.
💡Bayes Theorem Application
Bayes Theorem Application is the process of using Bayes Theorem to calculate conditional probabilities. In the video, the theorem is applied to determine the probability of having the virus given a positive test result. The script demonstrates how the theorem can be used to verify the intuitive calculations, showing the power of formal statistical methods in probability analysis.
Highlights

Introduction to Bayes Theorem and its application in conditional probability problems.

Example of using intuition to solve a conditional probability problem before applying Bayes Theorem.

Definition of the virus infection rate and test accuracy in terms of true positives and false positives.

Setting up the problem with events A (having the virus) and B (testing positive).

Organizing information in a 2x2 table to calculate conditional probabilities.

Calculating the expected number of people with the virus in a sample of 10,000.

Determining the number of true positives based on the infection rate and test accuracy.

Calculating the number of false positives among those who do not have the virus.

Finding the number of true negatives by subtracting false positives from the total without the virus.

Summing up the columns to verify the total number of people testing positive and negative.

Calculating the probability of having the virus given a positive test (P(A|B)).

Surprising result that only 4.09% of people who test positive actually have the virus.

Calculating the probability of not having the virus given a negative test (P(¬A|¬B)).

High accuracy of the test in determining who does not have the disease (99.6%).

Verification of the calculated probabilities using Bayes Theorem.

Discussion on the ease of using intuition vs. memorizing Bayes Theorem for solving problems.

Conclusion emphasizing the practical implications of the example and the value of the lesson.

Transcripts

Browse More Related Video

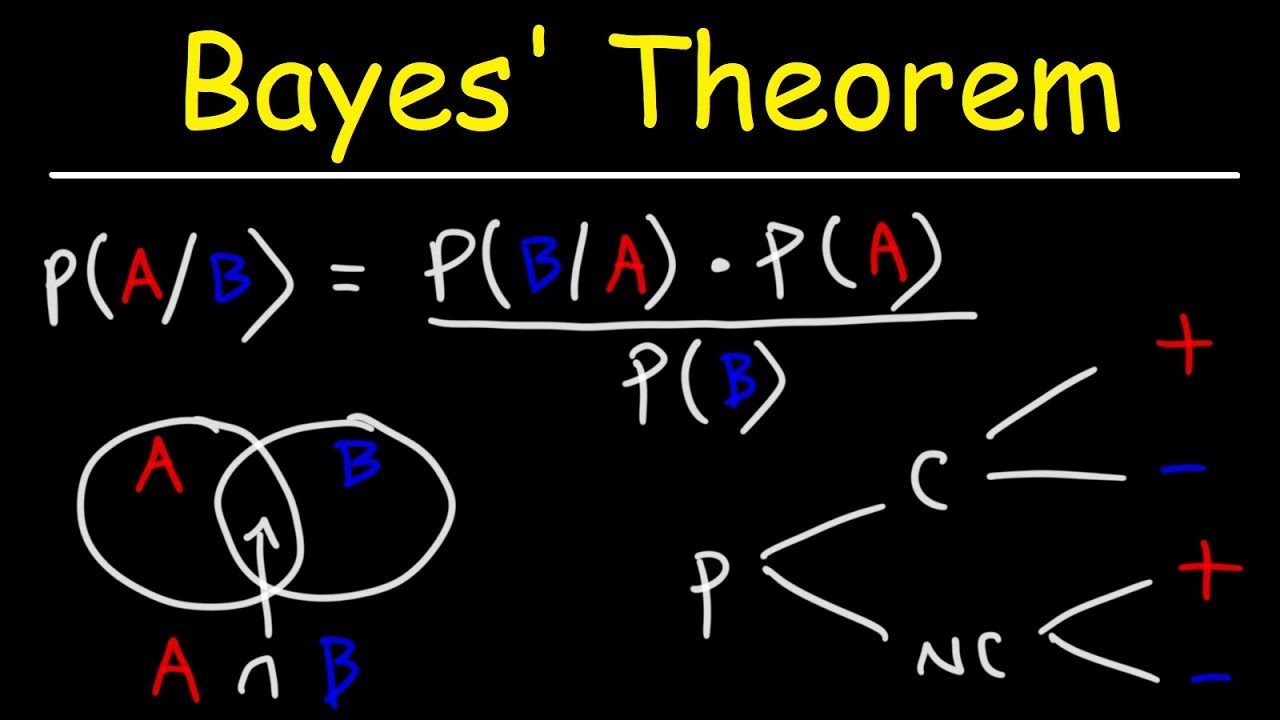
Bayes' Theorem of Probability With Tree Diagrams & Venn Diagrams

Probability Part 2: Updating Your Beliefs with Bayes: Crash Course Statistics #14

Bayes in Science and Everyday Life: Crash Course Statistics #25

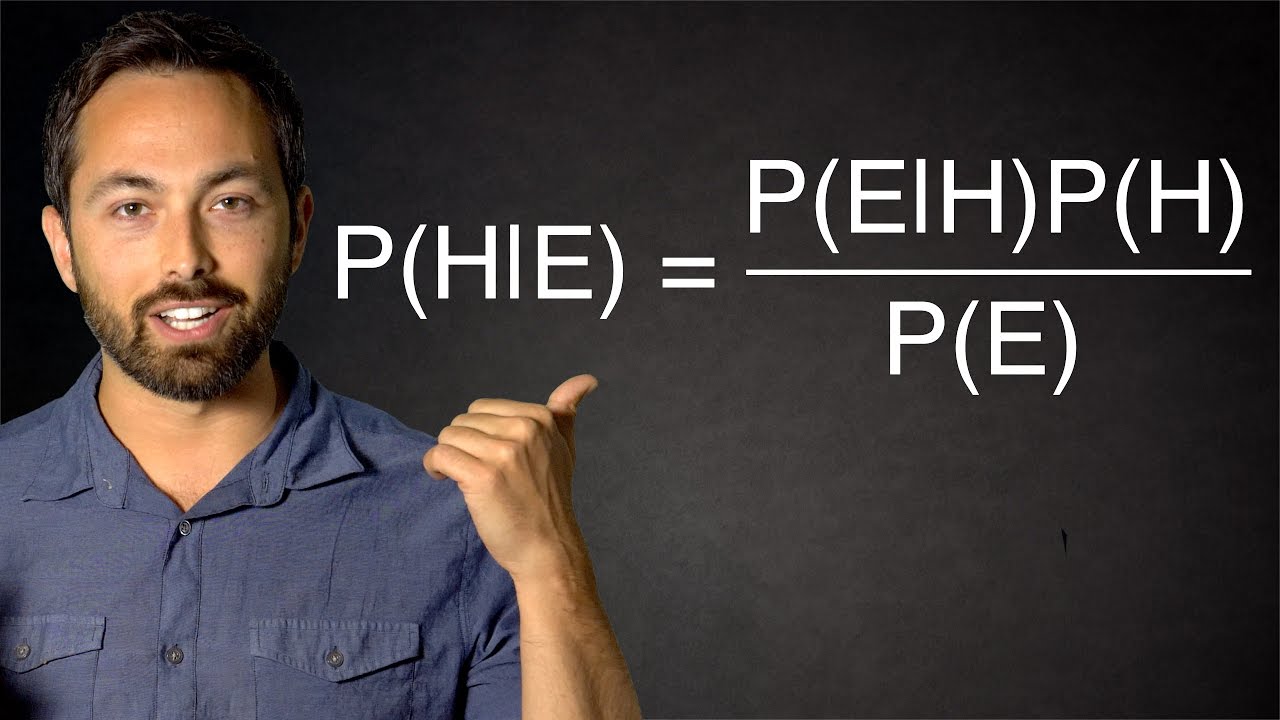
The Bayesian Trap

Probability Formulas, Symbols & Notations - Marginal, Joint, & Conditional Probabilities

Lecture 5: Conditioning Continued, Law of Total Probability | Statistics 110

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Bayes TheoremConditional ProbabilityVirus TestFalse PositivesTest AccuracyStatistical AnalysisProbability TheoryMedical TestingDisease DetectionHealthcare Insights