Die rolling probability | Probability and combinatorics | Precalculus | Khan Academy

Khan Academy
13 Jul 201505:14
EducationalLearning
32 Likes 10 Comments

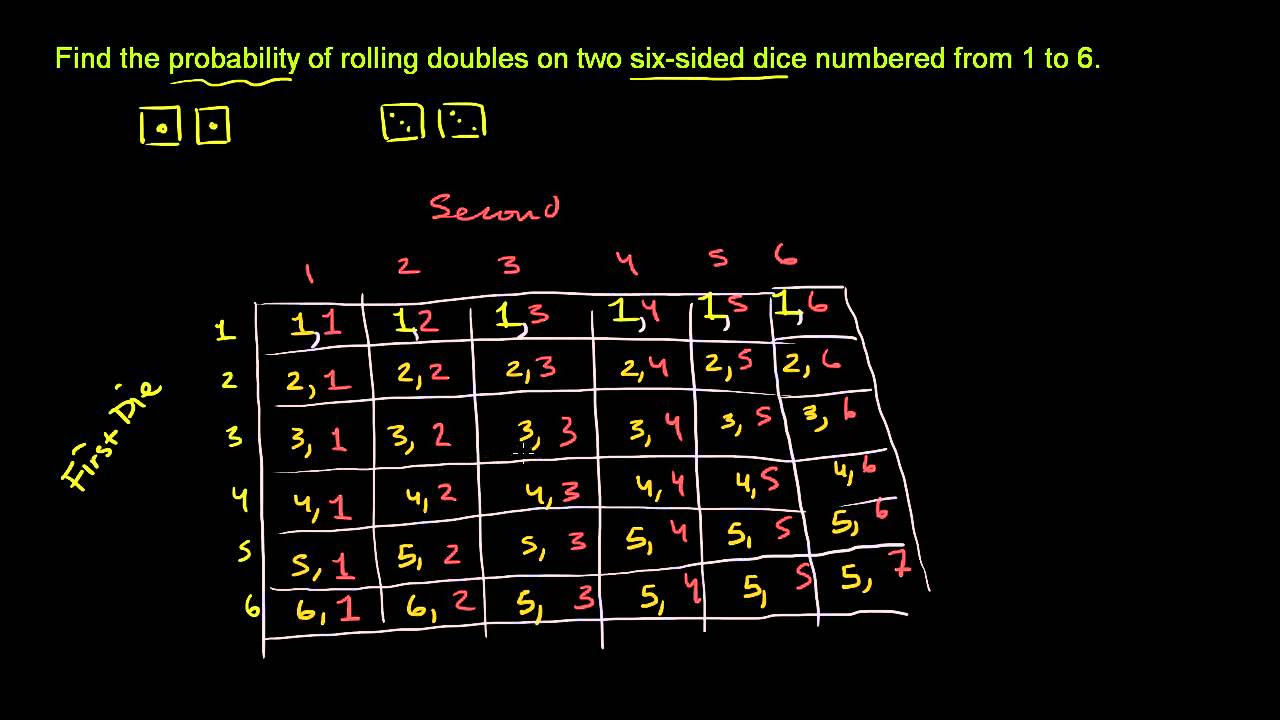
TLDRThis script explains how to calculate the probability of rolling doubles with two six-sided dice. It outlines the process of listing all possible outcomes and identifies those where both dice show the same number. With 36 total outcomes and 6 satisfying the condition of doubles (1-1, 2-2, 3-3, 4-4, 5-5, 6-6), the probability is calculated as 6/36, which simplifies to 1/6. Therefore, the probability of rolling doubles on two six-sided dice is 1/6.

Takeaways
  • 🎲 The event in question is rolling doubles on two six-sided dice numbered from 1 to 6.
  • 🧮 Rolling doubles means getting the same number on both dice, such as 1 and 1, 2 and 2, etc.
  • 📊 There are 36 possible outcomes when rolling two six-sided dice (6 sides per die).
  • 📝 The sample space for the first die is 1, 2, 3, 4, 5, 6.
  • 🔢 The sample space for the second die is also 1, 2, 3, 4, 5, 6.
  • 🔍 By creating a grid, we can visualize all possible outcomes of rolling two dice.
  • 📋 Each cell in the grid represents a unique outcome, such as (1,1), (1,2), etc.
  • ✅ There are 6 outcomes that satisfy the event of rolling doubles: (1,1), (2,2), (3,3), (4,4), (5,5), (6,6).
  • ⚖️ The probability of rolling doubles is calculated by dividing the number of successful outcomes (6) by the total number of possible outcomes (36).
  • ✔️ The probability of rolling doubles on two six-sided dice is 1/6.
Q & A

  • What does it mean to roll doubles on two six-sided dice?

    -Rolling doubles means that both dice show the same number on the top.

  • What are some examples of rolling doubles?

    -Examples include rolling a 1 and a 1, a 2 and a 2, a 3 and a 3, a 4 and a 4, a 5 and a 5, or a 6 and a 6.

  • How many possible outcomes are there when rolling two six-sided dice?

    -There are 36 possible outcomes, calculated as 6 (for the first die) times 6 (for the second die).

  • How can you visualize the possible outcomes of rolling two six-sided dice?

    -You can visualize the possible outcomes using a 6x6 grid, where each cell represents a combination of outcomes for the two dice.

  • How many outcomes satisfy the condition of rolling doubles?

    -There are 6 outcomes that satisfy the condition of rolling doubles.

  • What is the probability of rolling doubles on two six-sided dice?

    -The probability of rolling doubles is 1/6.

  • How do you calculate the probability of rolling doubles?

    -The probability is calculated by dividing the number of outcomes that satisfy the condition (6) by the total number of possible outcomes (36), which simplifies to 1/6.

  • What does the sample space represent in this context?

    -The sample space represents all possible outcomes when rolling two six-sided dice.

  • Why is it important to understand the sample space when calculating probabilities?

    -Understanding the sample space is important because it allows you to determine the total number of possible outcomes, which is necessary for calculating probabilities accurately.

  • Can you list the specific outcomes that represent rolling doubles?

    -The specific outcomes are (1,1), (2,2), (3,3), (4,4), (5,5), and (6,6).

Outlines
00:00
🎲 Understanding Probability of Rolling Doubles

The paragraph explains the concept of rolling doubles with two six-sided dice. Rolling doubles means getting the same number on both dice, such as 1 and 1, 2 and 2, etc. It outlines the sample space for rolling two dice, detailing the possible outcomes. A grid is drawn to visualize all potential outcomes, showing that there are 36 possible combinations when rolling two dice. The paragraph identifies that six of these combinations are doubles (1-1, 2-2, 3-3, 4-4, 5-5, 6-6).

05:02
📊 Calculating Probability

The paragraph concludes the explanation by calculating the probability of rolling doubles. With 6 favorable outcomes out of 36 possible outcomes, the probability is determined to be 6/36, which simplifies to 1/6. Therefore, the probability of rolling doubles on two six-sided dice is 1/6.

Mindmap
Keywords
💡Probability
Probability refers to the measure of the likelihood that a particular event will occur. In the context of this video, the event is rolling doubles on two six-sided dice. The script discusses calculating the probability of this event by comparing the number of favorable outcomes (rolling doubles) to the total number of possible outcomes (all combinations of dice rolls).
💡Doubles
Doubles in the context of dice rolling means obtaining the same number on both dice. For example, rolling a 1 and a 1, or a 3 and a 3. The video script uses this term to describe the specific outcome of interest when calculating the probability, emphasizing that only identical numbers on both dice count as doubles.
💡Six-sided dice
A six-sided die is a cube-shaped object used in games and probability calculations, with each face displaying a number from 1 to 6. The video script mentions these dice to set the stage for the probability problem, explaining that each die has six possible outcomes, which are crucial for determining the total number of possible outcomes when rolling two dice.
💡Sample space
The sample space is the set of all possible outcomes of an experiment, such as rolling dice. In the video script, the sample space is described by considering all combinations of rolls from the two six-sided dice, which totals 36 unique outcomes. This concept is fundamental in calculating probabilities, as it represents the denominator in the probability fraction.
💡Outcomes
Outcomes are the results of an event or experiment, such as the numbers shown on the top of the dice after a roll. The script discusses the outcomes in relation to the sample space, explaining that each roll of the dice results in an outcome and that these outcomes are used to determine the probability of rolling doubles.
💡Favorable outcomes
Favorable outcomes are those that meet the criteria of the event being considered. In this video, the favorable outcomes are the instances of rolling doubles. The script identifies these outcomes as the numerator in the probability calculation, as they are the specific results that contribute to the probability of the event occurring.
💡Grid
A grid is a visual representation used in the script to organize and display the possible outcomes of rolling two dice. It helps in systematically identifying each combination of dice rolls and visually distinguishing the favorable outcomes (doubles) from the total outcomes.
💡Total outcomes
Total outcomes refer to the sum of all possible results of an experiment, without any restrictions. The script calculates the total outcomes by multiplying the number of outcomes for each die (6), resulting in 36 possible combinations when rolling two six-sided dice. This total is essential for determining the probability of any event, including rolling doubles.
💡Event
An event in probability theory is a subset of the sample space that corresponds to a specific condition or occurrence. In the video script, the event is rolling doubles on two dice. The script uses this term to focus the discussion on the specific outcome of interest and to calculate the probability of this event happening.
💡Simplify
Simplifying in the context of the video script refers to the mathematical process of reducing a fraction to its lowest terms. The script shows that the probability of rolling doubles is initially calculated as 6/36, which is then simplified to 1/6. This simplification is crucial for understanding the final probability in its most reduced form.
Highlights

Rolling doubles means getting the same number on both dice.

Examples of doubles: 1 and 1, 2 and 2, 3 and 3, 4 and 4, 5 and 5, 6 and 6.

The event in question is rolling doubles on two six-sided dice numbered from 1 to 6.

Possible rolls for each die are 1, 2, 3, 4, 5, and 6.

There are 36 possible outcomes when rolling two six-sided dice.

The outcomes can be represented in a grid format for better visualization.

Each cell in the grid represents a unique outcome from rolling two dice.

Examples of outcomes: (1,1), (3,2), (4,5).

There are 6 outcomes that are doubles: (1,1), (2,2), (3,3), (4,4), (5,5), (6,6).

The number of outcomes that satisfy the criteria of rolling doubles is 6.

The total number of outcomes in the sample space is 36.

The probability of rolling doubles is calculated as the number of favorable outcomes divided by the total number of outcomes.

The probability of rolling doubles on two six-sided dice is 6/36.

6/36 simplifies to 1/6.

Therefore, the probability of rolling doubles on two six-sided dice is 1/6.

Transcripts

Browse More Related Video

Probability of More Complex Outcome

Find the equation of Hyperbola given vertices and asymptote

Probability of Complementary Events & Sample Space

Introduction to Probability, Basic Overview - Sample Space, & Tree Diagrams

Solving Quadratic Equations By Completing The Square

Multiplying Complex Numbers

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ProbabilityDiceStatisticsMathTutorialLearningEducationCalculationExampleExplanation