MATH1325 Lecture 10 2 - Concavity & Points of Inflection
TLDRThis lecture introduces the concept of concavity and points of inflection in the context of calculus for business and social science students. Concavity refers to the curvature of a function, with 'concave up' resembling a spoon that holds liquid, and 'concave down' like an inverted spoon that spills. The lecture explains that the first derivative indicates the slope of a function, while the second derivative helps determine concavity. A positive second derivative indicates a concave up function, and a negative one indicates concave down. Points of inflection, where the concavity changes, occur when the second derivative is zero. The lecture also applies these concepts to a real-life scenario of diminishing returns in profit, using the second derivative to find the point where profit growth begins to slow. The summary concludes with a reminder that the sign of the second derivative can help identify maximum or minimum points on a curve, with concave up indicating a minimum and concave down indicating a maximum.
Takeaways
- 📈 **Concavity Definition**: Concavity refers to the direction of a curve's bend, with 'concave up' resembling a spoon's shape when the curve points upwards, and 'concave down' when it points downwards.
- 🔍 **Tangent Lines and Concavity**: For a function to be concave up, the curve (f(x)) must lie above its tangent lines, and for concave down, below its tangent lines.
- 🔢 **Derivatives and Concavity**: The first derivative indicates the slope of a function, while the second derivative (f''(x)) determines concavity. If f''(x) is positive, the function is concave up; if negative, it's concave down.
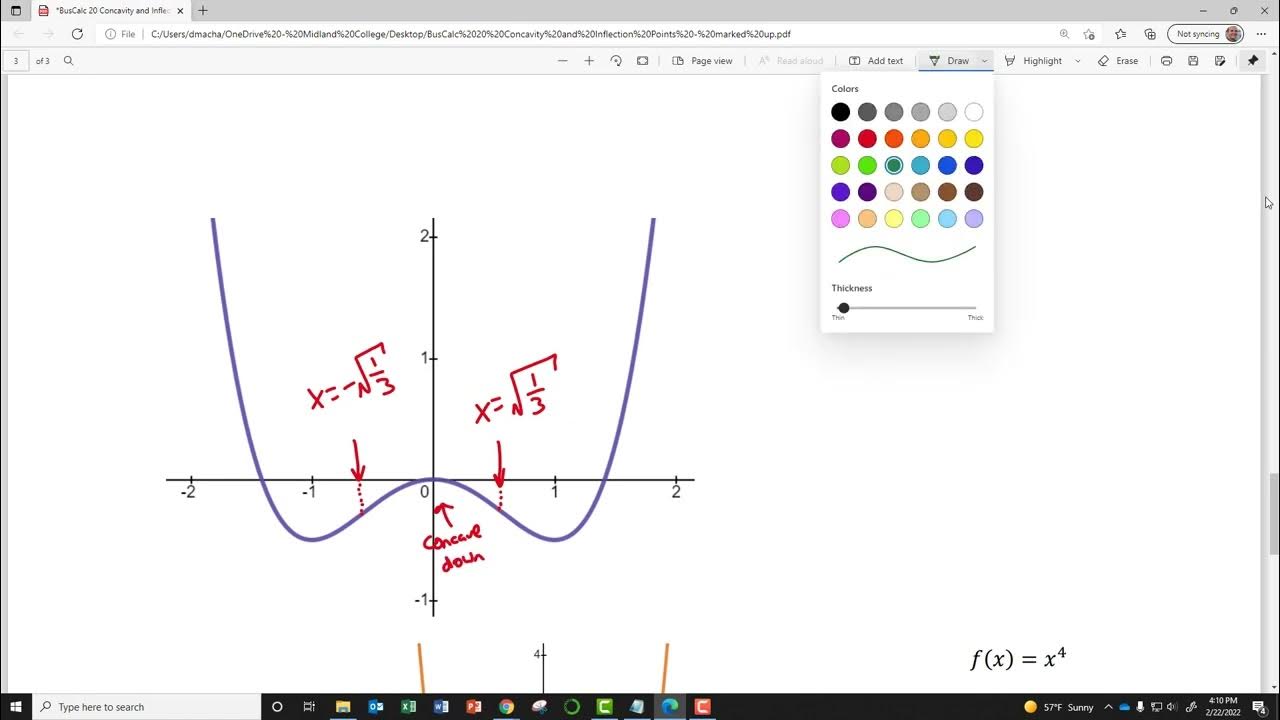
- 📌 **Points of Inflection**: These are the points where a function transitions from concave up to concave down or vice versa, marked by the second derivative being equal to zero.
- 🔧 **Finding Inflection Points**: To locate points of inflection, set the second derivative to zero and solve for x, then find the corresponding y-values by plugging these x-values back into the original function.
- 📉 **Profit and Diminishing Returns**: In business contexts, like profit functions, points of diminishing returns are identified as inflection points where the rate of profit growth begins to slow down.
- 🔺 **Second Derivative Test**: The second derivative can be used to test whether a critical point is a maximum or minimum. A positive second derivative at a point indicates a local minimum, while a negative second derivative indicates a local maximum.
- 📚 **Algebraic Simplification**: Simplifying the second derivative algebraically can reveal common factors that can be set to zero to find inflection points more easily.
- 🤔 **Critical Thinking**: It's important to consider both the sign of the second derivative and the context of the function when determining concavity and identifying points of inflection.
- 📊 **Graph Interpretation**: Visual inspection of the function's graph, along with its first and second derivatives, can provide a clearer understanding of concavity and points of inflection.
- ⚖️ **Balance Between Derivatives**: Remember that while the first derivative gives the slope, it's the second derivative that informs us about the concavity and the nature of the function's curvature.
Q & A
What is the concept of concavity in calculus?
-Concavity refers to the direction in which a curve bends. A function is said to be concave up when the curve bends like the back of a spoon with the 'C' facing upwards, and concave down when the 'C' is facing downwards, like an inverted spoon.
How does the concavity of a function relate to its tangent lines?
-For a function that is concave up, the function curve or f(x) lies above its tangent lines. Conversely, for a concave down function, the curve lies below the tangent lines.
How does the first derivative of a function indicate concavity?
-The first derivative gives the slope of the function. For a concave up function, the slope is increasing, which means going from larger negative values to smaller negative values, to zero, and then to positive values. For a concave down function, the slope is decreasing.
What is the role of the second derivative in determining concavity?
-The second derivative, which is the derivative of the first derivative, helps determine concavity. If the second derivative is positive over an interval, the original function is concave up over that interval. If the second derivative is negative, the function is concave down.
How can you find the points of inflection on a curve?
-Points of inflection are found where the second derivative is equal to zero. This is the point where the curve changes concavity, either from concave up to concave down or vice versa.
What does the sine curve demonstrate about concavity?
-The sine curve demonstrates that a function can move back and forth between concave up and concave down sections. It shows that there are points on the curve where it transitions from one type of concavity to the other.
What is the significance of the second derivative being zero at a point of inflection?
-The second derivative being zero at a point indicates a change in the concavity of the function. As you move from concave down to concave up (or vice versa), the second derivative transitions from positive to negative (or negative to positive), crossing zero at the point of inflection.
How can you determine if a point is a maximum or minimum by using the second derivative?
-If the second derivative at a critical point (where the first derivative is zero) is positive, the point is a local minimum. If the second derivative is negative, the point is a local maximum. This is known as the second derivative test.
What is the point of diminishing returns in the context of profit?
-The point of diminishing returns is the inflection point where profit growth begins to slow down. It represents the point after which the rate of increase in profit starts to decrease, even though the profit itself may continue to increase.
How does the second derivative help in understanding the behavior of a profit function over time?
-The second derivative of a profit function can indicate whether the rate of profit growth is increasing or decreasing. A positive second derivative indicates that the profit growth is itself increasing, while a negative second derivative means the rate of profit growth is slowing down.
What is the practical application of understanding concavity and points of inflection in business and social science?
-Understanding concavity and points of inflection can help in making informed decisions in business and social science. For example, in economics, it can help identify the optimal production levels or pricing strategies where marginal costs or benefits are at their most favorable points.
How does the shape of the second derivative graph relate to the concavity of the original function?
-The shape of the second derivative graph directly corresponds to the concavity of the original function. When the second derivative graph is above the x-axis, the original function is concave up, and when it is below the x-axis, the original function is concave down.
Outlines
📚 Introduction to Concavity and Points of Inflection
The first paragraph introduces the concept of concavity in calculus, drawing an analogy with the shape of a spoon to explain concave up and concave down curves. The lecturer explains that concave up occurs when the curve resembles a spoon with the 'C' pointing upwards, and the function's curve is above its tangent lines. Conversely, concave down is when the 'C' points downwards, and the curve is below the tangent lines. The role of derivatives is emphasized in determining concavity; specifically, the second derivative of a function is used to assess whether the function is concave up (increasing slope) or concave down (decreasing slope) over a given interval. The concept of a point of inflection, where the curve changes concavity, is also introduced, and it is identified by a second derivative equal to zero.
🔍 Finding Points of Inflection and Analyzing Concavity
The second paragraph delves into the process of finding points of inflection, which are the points where the curve transitions from concave up to concave down or vice versa. It is explained that these points occur where the second derivative of the function equals zero. The paragraph walks through an example of finding the second derivative of a given function, setting it to zero to solve for critical points, and then determining the concavity by examining the sign of the second derivative around these points. A real-life example involving the point of diminishing returns in profit is also discussed, where the second derivative is used to find the year when profit growth begins to slow down.
📈 Interpreting Second Derivatives and Profit Analysis
The third paragraph focuses on interpreting the second derivative in the context of profit functions. It explains that the second derivative's sign indicates whether the original function is concave up or down, which can be visualized by imagining a spoon holding or spilling its contents. The lecturer demonstrates how to find the second derivative of a profit function and use it to determine the point at which profit growth begins to slow (point of diminishing returns). The paragraph also includes an analysis of the profit function's graph, its first derivative, and the second derivative to illustrate the transition from concave up to concave down. Finally, it discusses how the second derivative can be used as a secondary test to determine if a critical point is a maximum or minimum.
Mindmap
Keywords
💡Concavity
💡Tangent Lines
💡Derivatives
💡Second Derivative
💡Points of Inflection
💡Sine Curve
💡Critical Values
💡Profit Function
💡Diminishing Returns
💡Optima Points
💡Number Line
Highlights
Concavity refers to the direction of the curve of a function, with 'concave up' indicating the curve resembles the shape of a spoon with the 'C' pointing upwards.
A function is concave up when its curve or f(x) is above its tangent lines, and concave down when below the tangent lines.
Derivatives help determine concavity; a function is concave up when its slope is always increasing, and concave down when the slope is always decreasing.
The second derivative, f''(x), is used to determine concavity; if positive over an interval, the function is concave up, and if negative, it is concave down.
A point of inflection is where a function changes concavity from concave up to down or vice versa, and it occurs when the second derivative equals zero.
The sine curve is an example of a function that moves back and forth between concave up and concave down.
To find points of inflection, set the second derivative equal to zero and solve for x, then find the corresponding y values from the original function.
The second derivative can also be used to determine if a critical point is a maximum or minimum by evaluating the sign of the second derivative at that point.
The point of diminishing returns in a profit function is an example of an inflection point where profit growth begins to slow down.
The annual profit function P(x) = -0.2x^3 + 3x^2 + 6, where x is the number of years past 2010, can be used to find the year when diminishing returns occur.
In the profit function example, the second derivative is used to find the year 2015 as the point where profit growth begins to slow.
Graphs of the profit function, its first derivative, and second derivative illustrate the transition from concave up to concave down at the point of inflection.
The first derivative represents the slope of the function, while the second derivative represents the rate of change of the slope.
The second derivative test is a quick way to determine if a critical point is a maximum or minimum without evaluating the function at the point.
A positive second derivative indicates a concave up function, which is analogous to a spoon holding its contents, while a negative second derivative indicates a concave down function.
The lecture provides a comprehensive understanding of how to use derivatives to analyze the concavity and points of inflection in calculus for business and social science applications.
Transcripts
Browse More Related Video

Concavity introduction | Using derivatives to analyze functions | AP Calculus AB | Khan Academy

Calculus 1: Concavity Examples

Concavity and the 2nd Derivative Test

Concavity, Inflection Points, and Second Derivative
BusCalc 20 Concavity and Inflection Points

Business Calculus - Math 1329 - Section 3.2 - Concavity and Points of Inflection
5.0 / 5 (0 votes)
Thanks for rating: