2015 #5 Free Response Question - AP Physics 1 - Exam Solution

Flipping Physics
7 Apr 201606:14
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, the host tackles a 2015 AP Physics 1 exam question involving a string attached to a frequency oscillator and a block with mass, creating a standing wave. The discussion covers the relationship between wave velocity, frequency, wavelength, and linear mass density, and how these factors affect the fundamental frequencies of different strings. The video also explores the graphing of frequency against the inverse of linear mass density and identifies the points of greatest average vertical speed in the second harmonic of a string.

Takeaways
  • 🎓 The video discusses solving a free response question from the 2015 AP Physics 1 exam.
  • 🎵 The Flipping Physics channel is mentioned, indicating the educational nature of the content.
  • 📚 A string is attached to a frequency oscillator on one end and a block with mass (M) on the other, with a pulley in between.
  • 🎶 The oscillator is set to oscillate at a frequency that creates a standing wave, specifically the fundamental frequency, in the string.
  • 🔍 There are four different lab setups with varying strings and fundamental frequencies.
  • 📘 An equation for the velocity of a wave on a string is provided, involving the force of tension and the linear mass density.
  • 🔢 The lowercase 'm' in the equation represents the mass per unit length of the string, distinct from the uppercase 'M' representing the block's mass.
  • 🎼 Part A of the question asks why the four strings have different fundamental frequencies, which is explained through the relationship between velocity, frequency, and wavelength.
  • 📊 Part B explores whether a graph of frequency versus the inverse of linear mass density would be linear, concluding that it would not due to the squared relationship.
  • 🎵 Part C involves changing the frequency of the oscillator for string D to its second harmonic, and identifying the points on the string with the greatest average vertical speed, which are the antinodes.
  • 🏁 The video concludes with an invitation to watch review videos covering all AP Physics 1 topics, suggesting further educational resources.
Q & A

  • What is the main topic of the video?

    -The video discusses solving a free response question from the 2015 AP Physics 1 exam, specifically focusing on the properties of a string attached to a frequency oscillator and a block, and how these properties affect the fundamental frequency of the string.

  • What is the fundamental frequency in the context of the video?

    -The fundamental frequency refers to the lowest frequency at which a string can vibrate to produce a standing wave, which is the scenario described in the video.

  • What is the relationship between the velocity of a wave on a string and the force of tension?

    -The velocity of a wave on a string is equal to the square root of the force of tension in the string divided by the mass per unit length of the string, also known as the linear mass density.

  • Why are there different fundamental frequencies in the four strings described in the video?

    -The different fundamental frequencies result from the different linear mass densities of the strings, despite having the same length and the same mass attached to their ends.

  • What is the role of the mass attached to the end of the string in determining the velocity of the wave on the string?

    -The mass attached to the end of the string, denoted as capital M, affects the force of tension in the string, which in turn influences the velocity of the wave on the string.

  • How does the wavelength of a wave relate to its frequency and velocity?

    -The wavelength of a wave is directly proportional to its frequency and inversely proportional to its velocity, as described by the equation velocity = frequency × wavelength.

  • Why would the graph of frequency as a function of the inverse of the linear mass density not be linear?

    -The graph would not be linear because the relationship derived from the equations shows that frequency squared is proportional to the inverse of the linear mass density, not frequency itself.

  • What is the significance of antinodes in a standing wave?

    -Antinodes are points on a standing wave where the amplitude is maximum, and they are locations of greatest average vertical speed.

  • How does changing the frequency of the oscillator affect the string's vibration?

    -Changing the frequency of the oscillator to a higher value, such as to the second harmonic, changes the number of nodes and antinodes in the standing wave, affecting the pattern of vibration.

  • What are the points on the string that have the greatest average vertical speed when the string vibrates in its second harmonic?

    -When the string vibrates in its second harmonic, the points of greatest average vertical speed are located at the antinodes, which are halfway between the nodes.

  • What is the educational value of the video in terms of physics concepts?

    -The video provides a practical application of physics concepts such as wave velocity, frequency, wavelength, and the properties of standing waves, which are crucial for understanding AP Physics 1 topics.

Outlines
00:00
🎓 Physics Exam Question Analysis

This paragraph introduces a problem from the 2015 AP Physics 1 exam. The scenario involves a string attached to a frequency oscillator on one end and a block with mass (M) on the other, passing over a frictionless pulley. The string is set to vibrate at its fundamental frequency, creating a standing wave. There are four similar setups with different strings and fundamental frequencies. The velocity of a wave on a string is given by the square root of the force of tension divided by the linear mass density. The lowercase 'm' in the equation represents the mass per unit length of the string, while the uppercase 'M' represents the mass of the block. The paragraph discusses the expectation of encountering unfamiliar equations on the AP test and introduces the first part of the question, which asks why the four strings have different fundamental frequencies.

05:01
📚 Understanding Wave Velocity and Frequency

In this paragraph, the discussion focuses on the relationship between wave velocity, frequency, wavelength, and linear mass density. It explains that the four strings have the same length and are vibrating at their fundamental frequencies, implying the same wavelength. However, they have different frequencies, leading to different wave velocities. Since the mass (M) attached to each string is the same, the force of tension is also the same. Using the given equation, it is deduced that the different wave velocities must be due to different linear mass densities of the strings. The paragraph also addresses a student's question about graphing frequency as a function of the inverse of linear mass density, concluding that the graph would not be linear due to the relationship involving the square of frequency. Finally, the paragraph touches on the concept of standing waves and harmonics, explaining that the second harmonic of a string increases the number of nodes and antinodes, with the greatest average vertical speed occurring at the antinodes.

Mindmap
Keywords
💡Frequency Oscillator
A frequency oscillator is a device that generates periodic signals at a specific frequency. In the context of the video, it is attached to one end of a string and is used to create a standing wave by oscillating at the string's fundamental frequency. This device is central to the experiment as it influences the wave properties of the string.
💡Standing Wave
A standing wave is a wave that appears to be standing still, with nodes and antinodes that do not move along the medium. In the video, a standing wave is set up in the string by the frequency oscillator, which is crucial for understanding the fundamental frequency and the behavior of waves on a string.
💡Fundamental Frequency
The fundamental frequency is the lowest frequency at which a system can vibrate. In the script, the frequency oscillator is set to the fundamental frequency to create the first harmonic standing wave on the string, which is a key concept in understanding the lab setup and the physics behind it.
💡Linear Mass Density
Linear mass density refers to the mass per unit length of a material and is denoted by the lowercase 'm' in the script. It is a crucial parameter in determining the wave velocity on a string, as shown in the provided equation, and is different for each string in the lab setup, leading to different fundamental frequencies.
💡Wave Velocity
Wave velocity is the speed at which a wave propagates through a medium. In the video, the velocity of a wave on a string is given by the square root of the force of tension divided by the linear mass density. This concept is central to solving the problems presented in the script, as it relates to the tension in the string and the mass of the string.
💡Tension
Tension is the force exerted by a string when it is pulled tight by opposing forces. In the context of the video, the force of tension in the string is a factor in the equation for wave velocity and is assumed to be the same for each string due to the same mass attached at the end.
💡Mass
In the script, 'mass' refers to two different concepts: the lowercase 'm' for the mass per unit length of the string and the capital 'M' for the mass of the block attached to the string. The mass of the block is constant across different strings, while the mass per unit length varies, affecting the fundamental frequency.
💡Harmonic
A harmonic is a frequency that is an integer multiple of the fundamental frequency. In the video, the second harmonic is mentioned, which is the frequency at which the string vibrates with three nodes and two antinodes, doubling the number of nodes and antinodes from the fundamental frequency.
💡Antinode
An antinode is a point on a standing wave where the amplitude is at its maximum. In the script, the locations of the antinodes are identified as having the greatest average vertical speed when the string is vibrating at its second harmonic.
💡Node
A node is a point on a standing wave where there is no displacement; the amplitude is zero. In the context of the video, the fundamental frequency has two nodes, while the second harmonic has three nodes, which changes the pattern of the standing wave.
💡Graph
In the script, a student is asked to graph frequency as a function of the inverse of the linear mass density. The expectation is that the graph will not be linear due to the relationship between frequency and the square of the inverse of linear mass density, as derived from the wave velocity equation.
Highlights

Introduction to solving free response question number five from the 2015 AP Physics 1 exam.

Description of the lab setup involving a string, frequency oscillator, and a mass block with a pulley.

Explanation of the fundamental frequency and standing wave in the string.

Mention of four different lab setups with varying strings and fundamental frequencies.

Introduction of the equation for the velocity of a wave on a string.

Clarification on the distinction between lowercase m (mass per unit length) and capital M (mass of the block).

Discussion on the expectation to use knowledge beyond the curriculum in AP tests.

Part A of the question asks about differences in strings leading to different fundamental frequencies.

Explanation that each string vibrates at its fundamental frequency with the same length and wavelength.

Insight that the velocity of the wave on each string must be different due to different frequencies.

Argument that the mass per unit length must vary for different strings to achieve different velocities.

Part B of the question involves graphing frequency as a function of the inverse of linear mass density.

Derivation showing that the graph will not be linear due to the relationship between frequency squared and linear mass density.

Part C of the question changes the frequency of the oscillator to make the string vibrate in its second harmonic.

Identification of antinodes as locations of greatest average vertical speed in a standing wave.

Description of the second harmonic having three nodes and two antinodes.

Conclusion that the greatest average vertical speed points are at the two antinodes in the string.

Invitation to watch review videos covering every AP Physics 1 topic.

Transcripts

Browse More Related Video

2015 AP Physics 1 free response 5

2015 AP Physics 1 Free Response #5

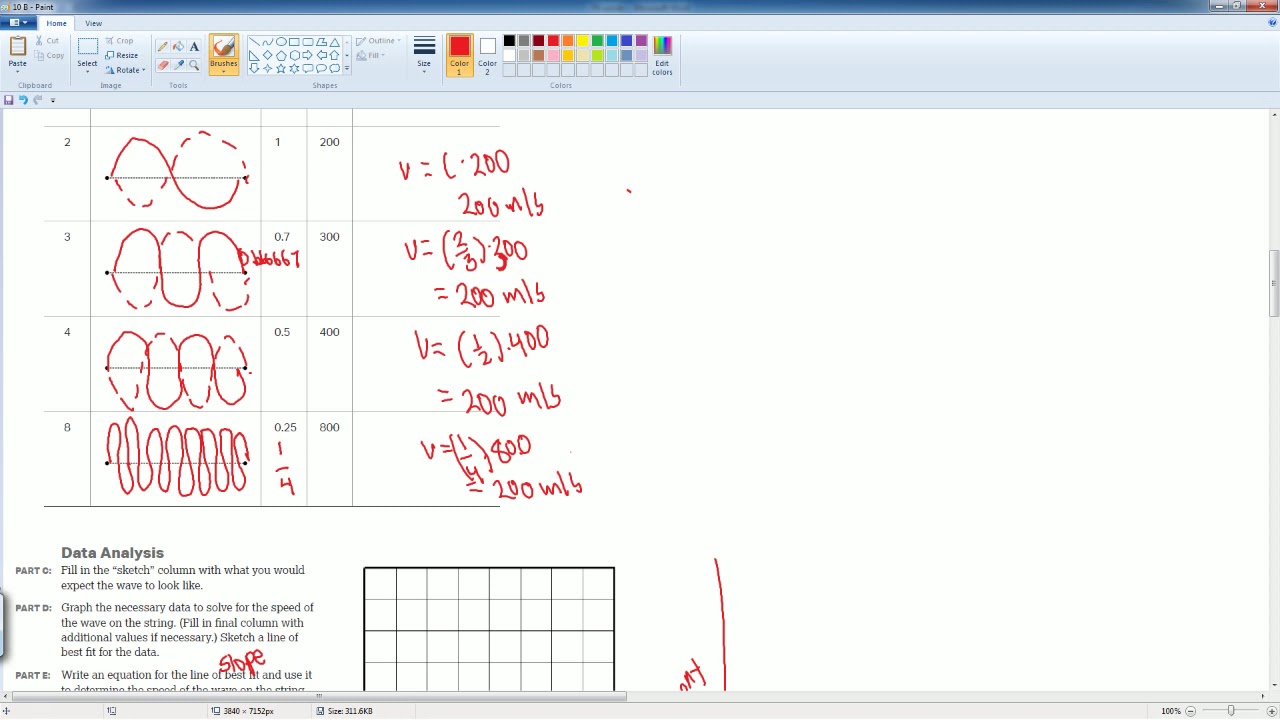
AP Physics Workbook 10.B Relationship Between Wave Speed, Frequency, and Wavelength

Wave Speed on a String - Tension Force, Intensity, Power, Amplitude, Frequency - Inverse Square Law

AP Physics 1 review of Waves and Harmonic motion | Physics | Khan Academy

AP Physics Workbook 10.A Properties of a Wave

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ExamString VibrationFundamental FrequencyStanding WaveWave VelocityLinear Mass DensityTension ForceHarmonic WavesAP ReviewEducational Content