Parallel Lines and Perpendicular Lines - Nerdstudy

Nerdstudy
11 Feb 201705:34
EducationalLearning
32 Likes 10 Comments

TLDRThis video explores the relationship between the slopes of parallel and perpendicular lines. It explains that parallel lines have identical slopes, while perpendicular lines have slopes that are negative reciprocals of each other. The video uses graphical examples to illustrate these concepts and concludes with a practical exercise to identify a line perpendicular to a given equation.

Takeaways
  • 📚 Parallel lines are defined by having the same slope. This means that for every unit change in x, y changes by the same amount.
  • 📈 The slope of a line is calculated as the change in y values divided by the change in x values. For example, if y increases by 2 units for every 1 unit increase in x, the slope is 2.
  • 🔍 The slope-intercept form of a line's equation is y = mx + b, where m is the slope and b is the y-intercept.
  • 🔄 Changing the slope of a line will eventually cause it to intersect with another line, making them no longer parallel.
  • 🔄 Increasing or decreasing the slope of a line from its original value will disrupt the parallel nature of the lines.
  • 📐 Perpendicular lines intersect at a 90° angle. They are not parallel and their slopes are related in a specific way.
  • 🔄 The slope of a line perpendicular to another is the negative reciprocal of the original line's slope. For example, if one line has a slope of 3, the perpendicular line's slope would be -1/3.
  • 🔍 To find the equation of a line perpendicular to another, you take the negative reciprocal of the original line's slope and use it in the slope-intercept form.
  • 📚 Remembering that parallel lines have identical slopes and perpendicular lines have slopes that are negative reciprocals of each other is crucial for understanding their geometric relationships.
  • 🤓 Engaging in more practice with questions and problems will help solidify the understanding of these concepts.
Q & A

  • What is the definition of parallel lines?

    -Parallel lines are lines in a plane that do not meet; they are always the same distance apart and will never intersect.

  • How is the slope of a line defined?

    -The slope of a line is defined as the ratio of the change in y-values to the change in x-values, or rise over run.

  • What is the slope of a line if it goes one unit to the right on the x-axis and two units up on the y-axis?

    -The slope of the line would be 2 over 1, or simply 2.

  • What is the slope-intercept form of a line and how is it used?

    -The slope-intercept form of a line is written as y = mx + b, where m is the slope and b is the y-intercept. It is used to write the equation of a line when you know its slope and y-intercept.

  • Why do parallel lines have the same slope?

    -Parallel lines have the same slope because they run in the same direction with the same steepness, ensuring they never intersect.

  • What happens if you change the slope of a line that is parallel to another?

    -Changing the slope of a line that is parallel to another will eventually cause the lines to intersect, making them no longer parallel.

  • What is a perpendicular line?

    -A perpendicular line is a line that intersects another line at a 90° angle.

  • How are the slopes of perpendicular lines related?

    -The slopes of perpendicular lines are negative reciprocals of each other. If one line has a slope of m, the perpendicular line will have a slope of -1/m.

  • If a line has a slope of 3, what would be the slope of a line perpendicular to it?

    -The slope of a line perpendicular to one with a slope of 3 would be -1/3.

  • What is the equation of a line perpendicular to y = 1/2x + 4?

    -The equation of a line perpendicular to y = 1/2x + 4 would be y = -2x + 4, as the slope of the perpendicular line is the negative reciprocal of 1/2, which is -2.

  • Why do perpendicular lines intersect at a 90° angle?

    -Perpendicular lines intersect at a 90° angle because their slopes are negative reciprocals, which geometrically results in a right angle intersection.

Outlines
00:00
📏 Understanding Parallel and Perpendicular Lines

This paragraph introduces the concept of parallel and perpendicular lines in geometry. It explains that parallel lines have the same slope, demonstrated by drawing two lines on a graph and showing how their y-values change proportionally with x-values. The slope is calculated as the change in y divided by the change in x, and the slope-intercept form of the equation is used to represent these lines. The paragraph also clarifies that changing the slope of a line would result in it no longer being parallel to another line. Additionally, the concept of perpendicular lines is introduced, which intersect at a 90° angle, and their slopes are the negative reciprocals of each other.

05:01
📐 Calculating Perpendicular Line Equations

This paragraph focuses on the relationship between the slopes of perpendicular lines. It emphasizes that perpendicular lines have slopes that are negative reciprocals of each other. The explanation includes a step-by-step process of finding the slope of a perpendicular line given the slope of another line. An example is provided where the slope of a line is 1/2, and the perpendicular line's slope is calculated as -2. The paragraph concludes with an exercise where the viewer is asked to determine which line would be perpendicular to a given line, and the correct answer is identified as the one with a slope of -2.

Mindmap
Keywords
💡Parallel Lines
Parallel lines are two lines in a plane that never intersect, no matter how far they are extended. In the video, the concept is introduced by drawing two lines on a graph and observing that they maintain a constant distance from each other. The script explains that all parallel lines have the same slope, which is a key characteristic that defines their parallel nature. For example, the script mentions that if you change the slope of one line, it will no longer be parallel to the other.
💡Slope
Slope is a measure of the steepness of a line, defined as the ratio of the change in the y-coordinate to the change in the x-coordinate between any two points on the line. In the context of the video, the slope is used to determine whether lines are parallel or perpendicular. The script demonstrates that a line with a slope of 2/1 is parallel to another line with the same slope, and that changing the slope would result in the lines intersecting and no longer being parallel.
💡Y-Intercept
The y-intercept is the point where a line crosses the y-axis in a Cartesian coordinate system. It is a key component in the slope-intercept form of a line equation, y = mx + b, where b represents the y-intercept. In the video, the y-intercept is used to distinguish between parallel lines that have different starting points on the y-axis, such as lines with y-intercepts at 0 and 3.
💡Slope-Intercept Form
The slope-intercept form of a linear equation is y = mx + b, where m represents the slope and b represents the y-intercept. This form is used in the video to derive the equation of a line given its slope and y-intercept. For instance, the script uses the slope-intercept form to write the equation of a line with a slope of 2 and a y-intercept of 1 as y = 2x + 1.
💡Perpendicular Lines
Perpendicular lines are two lines that intersect at a 90° angle. The video explains that perpendicular lines have slopes that are negative reciprocals of each other. This means that if one line has a slope of m, the perpendicular line will have a slope of -1/m. The script uses this concept to determine which line would be perpendicular to a given line with a slope of 1/2.
💡Negative Reciprocal
The negative reciprocal of a number is obtained by multiplying the number by -1 and then taking the reciprocal. In the context of slopes, if one line has a slope of m, the negative reciprocal slope is -1/m. This concept is crucial in determining the slope of a line that is perpendicular to another. The video uses the negative reciprocal to find the slope of a line perpendicular to one with a slope of 1/2, resulting in a slope of -2.
💡Intersection
Intersection refers to the point or points where two lines meet. In the video, the concept is discussed in relation to parallel and perpendicular lines. Parallel lines do not intersect, while perpendicular lines intersect at a 90° angle. The script illustrates that changing the slope of a line can cause it to intersect with another line, thereby making them not parallel.
💡Equation of a Line
The equation of a line is a mathematical representation of the relationship between the x and y coordinates of points on the line. In the video, the equation of a line is derived using the slope-intercept form, which is y = mx + b. The script shows how to find the equation of a line by plugging in the slope and y-intercept values, such as y = 2x + 1 for a line with a slope of 2 and a y-intercept of 1.
💡Cartesian Coordinate System
A Cartesian coordinate system is a two-dimensional plane where points are defined by their x and y coordinates. The video uses this system to graph lines and discuss their properties, such as parallelism and perpendicularity. The script demonstrates how lines are represented in this system and how their slopes and y-intercepts can be determined from their graphical representation.
💡Graphical Representation
Graphical representation involves visually depicting mathematical concepts or relationships, such as lines, on a graph. In the video, the script uses graphical representation to illustrate the properties of parallel and perpendicular lines. The script shows how to draw lines on a graph and observe their slopes and y-intercepts, which helps in understanding their mathematical properties.
Highlights

Introduction to the concept of parallel and perpendicular lines and their slopes.

Drawing two parallel lines on a graph and explaining their slope.

Demonstration of how a change in x results in a change in y, leading to a slope of 2/1.

Equation of a line using the slope-intercept form with a slope of 2 and y-intercept of 0.

Observation of a second parallel line with a y-intercept at 0.3 and the same slope of 2.

Explanation that all parallel lines have the same slope.

Illustration of how changing the slope of a line would make it non-parallel.

Visual representation of the importance of maintaining the same slope for parallel lines.

Introduction to the concept of perpendicular lines intersecting at a 90° angle.

Graphical representation of perpendicular lines and their relationship.

Explanation of negative reciprocal slopes for perpendicular lines.

Example of finding the slope of a perpendicular line given a slope of 3.

Demonstration of calculating the negative reciprocal slope as -1/3.

Providing an equation for a line perpendicular to a given line with a slope of 1/2.

Simplification of the perpendicular slope to -2 and the equation Y = -2x + 4.

Summary of the key points: parallel lines have the same slopes, and perpendicular lines have slopes that are negative reciprocals.

Encouragement to practice with more questions to reinforce understanding.

Transcripts

Browse More Related Video

Graphing Parallel and Perpendicular Lines

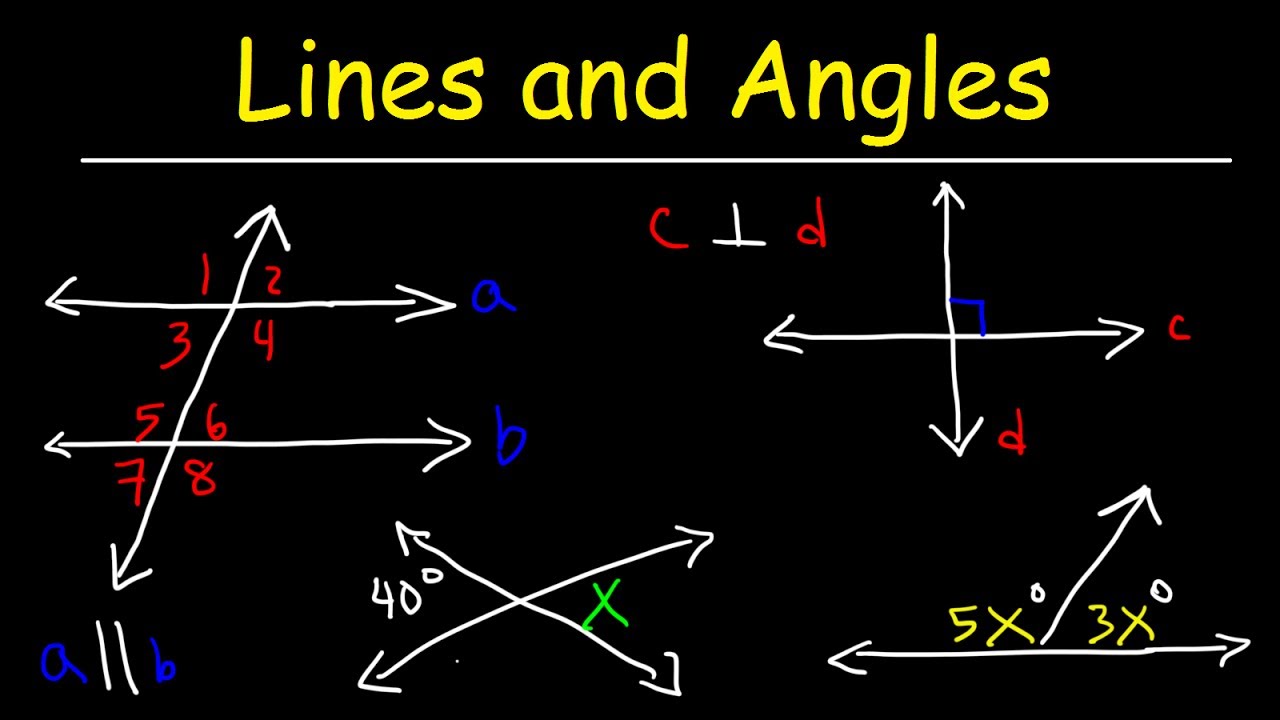
Parallel and Perpendicular Lines, Transversals, Alternate Interior Angles, Alternate Exterior Angles

Parallel, Intersection and Perpendicular Line

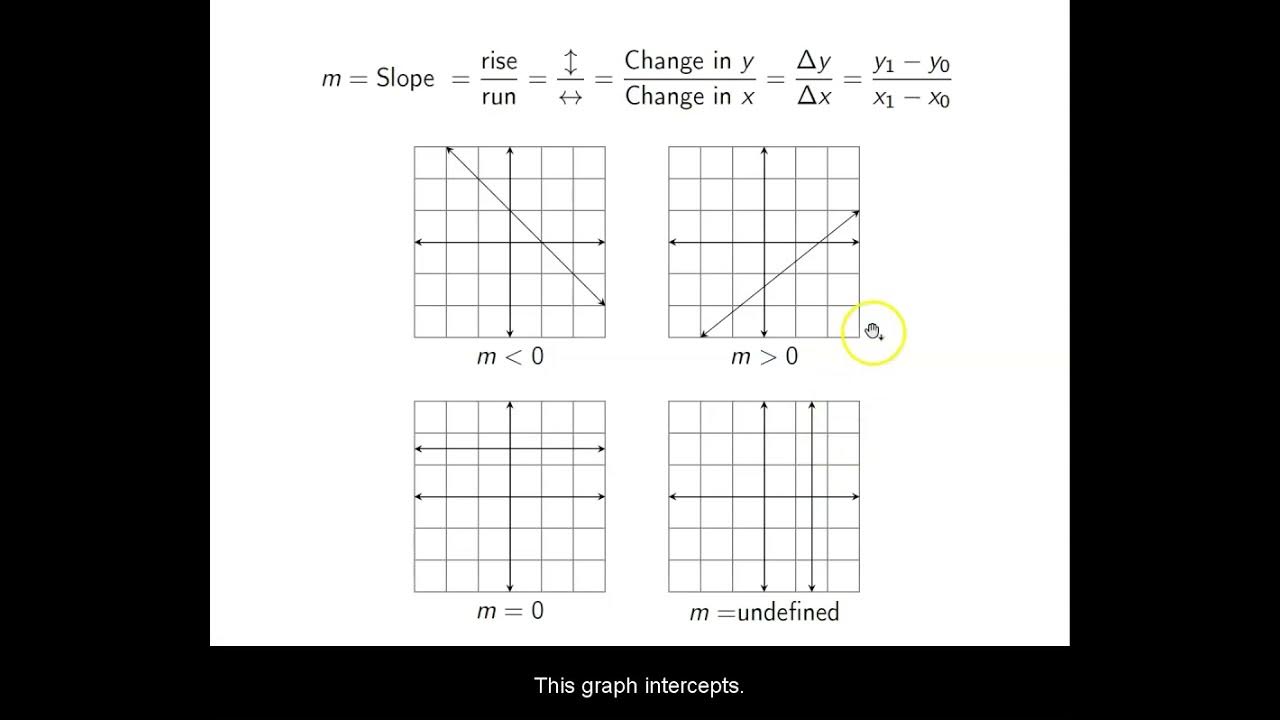
Ch. 1.10 Lines

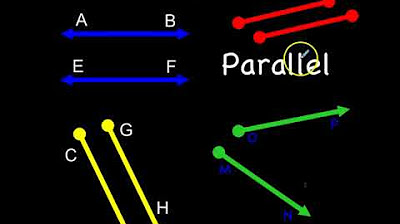
Parallel, Intersecting, & Perpendicular Lines

Parallel, Intersecting, and Perpendicular Lines | Geometry | Math with Mr. J

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
GeometrySlopeParallel LinesPerpendicular LinesMath EducationGraph AnalysisSlope InterceptNegative ReciprocalLine IntersectionEducational Content