Adding Vectors Example | Physics with Professor Matt Anderson | M3-10
TLDRThe script presents a step-by-step guide to solving a vector-based problem involving running in different directions. It begins by establishing a coordinate system and defining movements as vectors, then calculating the resultant vector to determine the final distance and direction from the starting point. The process involves visualizing the movements, calculating the magnitude of the resultant vector, and determining the angle using trigonometric relations. The problem is solved by finding the displacement north and west, and finally, the angle is described as 23.3 degrees west of north, highlighting the importance of specifying the quadrant for accurate description.
Takeaways
- 📍 The problem involves running a series of distances in different directions: 1 mile north, 0.4 miles west, and 0.1 miles south.
- 📐 A coordinate system is used to visualize the movements, with the initial point as the origin.
- 🔍 The first movement is one mile north, represented by vector 'a'.
- 🔍 The second movement is 0.4 miles west, represented by vector 'b'.
- 🔍 The final movement is 0.1 miles south, represented by vector 'c'.
- 🧮 The total displacement north is calculated by subtracting the southward movement (0.1 miles) from the initial northward movement (1 mile), resulting in 0.9 miles.
- 🧮 The total displacement west is the only westward movement, which is 0.4 miles.
- 📊 The resultant vector 'r' is found by using the Pythagorean theorem on the lengths of the displacements: sqrt(0.9^2 + 0.4^2), which approximates to 1.04 miles.
- 📈 The angle from the initial direction is calculated using trigonometry, with the cosine of the angle being the adjacent side (0.9 miles) divided by the hypotenuse (1.04 miles).
- 📐 The angle is found to be approximately 23.3 degrees, which is described as 'west of north'.
- 🌟 The concept of specifying angles with regards to 'north, east, south, west' is emphasized, with the final angle described as 23.3 degrees west of north.
- 🔄 The lesson also touches on the concept of converting angles to different reference points, such as describing an angle as 'north of northwest' or 'east of south', and the importance of clarity in these descriptions.
Q & A
What is the first direction the speaker runs in?
-The first direction the speaker runs in is one mile north.
How far does the speaker run in the second segment?
-In the second segment, the speaker runs 0.4 miles west.
What is the final distance run in the third part of the journey?
-In the third part of the journey, the speaker runs 0.1 miles south.
What is the total displacement north after all three segments?
-The total displacement north is 0.9 miles, as the speaker initially runs 1 mile north and then goes 0.1 mile south.
What is the total displacement west?
-The total displacement west is 0.4 miles, which is the distance run in the second segment.
How is the resultant vector labeled in the script?
-The resultant vector is labeled as 'r' in the script.
What is the total distance 'r' from the starting point?
-The total distance 'r' from the starting point is approximately 0.98 miles.
How is the angle 'phi' calculated?
-The angle 'phi' is calculated using the cosine of the angle, which is the adjacent side (0.9 miles) divided by the hypotenuse (0.98 miles), and then taking the arc cosine of that value.
What is the final calculated angle 'phi'?
-The final calculated angle 'phi' is 23.3 degrees.
How is the 23.3 degrees angle described in terms of cardinal directions?
-The 23.3 degrees angle is described as '23.3 degrees west of north'.
What would be the angle if described as 'north of northwest'?
-If described as 'north of northwest', the angle would be 113.3 degrees, following the rule of starting from north and rotating 23.3 degrees towards the west.
Why is it important to specify the quadrant when giving an angle in degrees?
-Specifying the quadrant is important because it provides clarity on the direction of the angle, especially when dealing with angles that are not multiples of 45 degrees, which would be easily identifiable as north, east, south, or west.
Outlines
🏃♂️ Running a Triangular Course
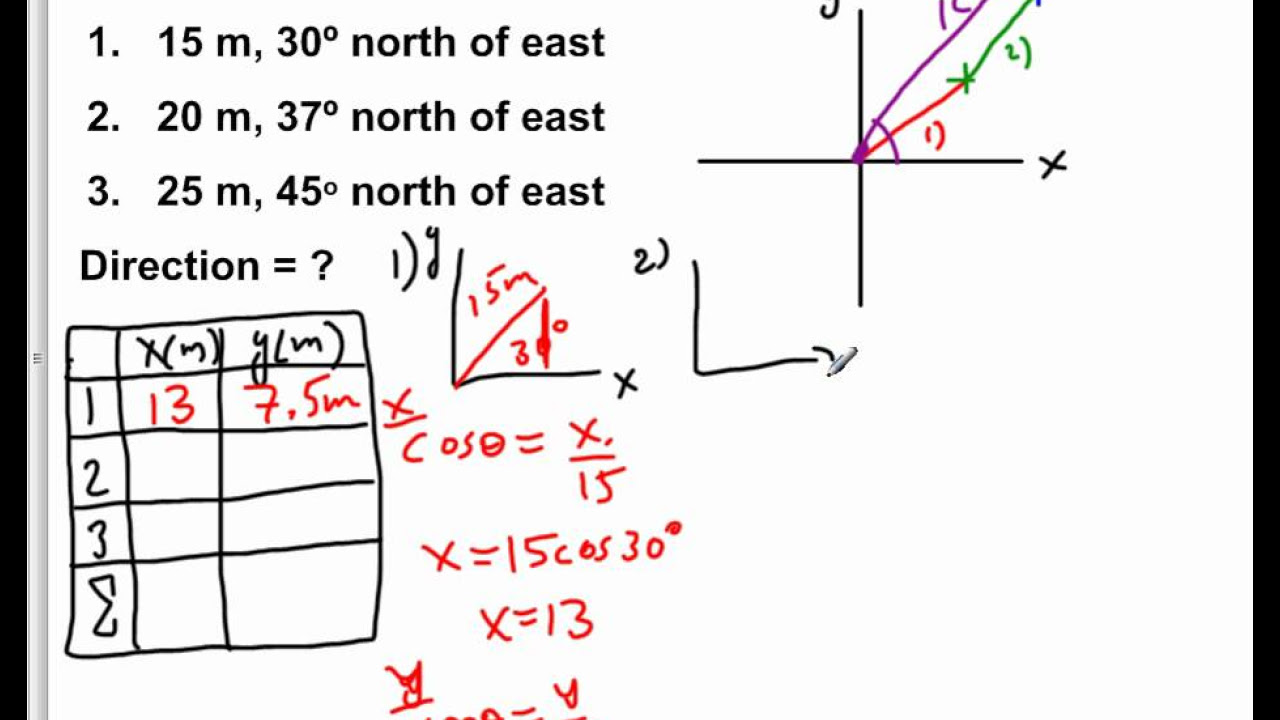
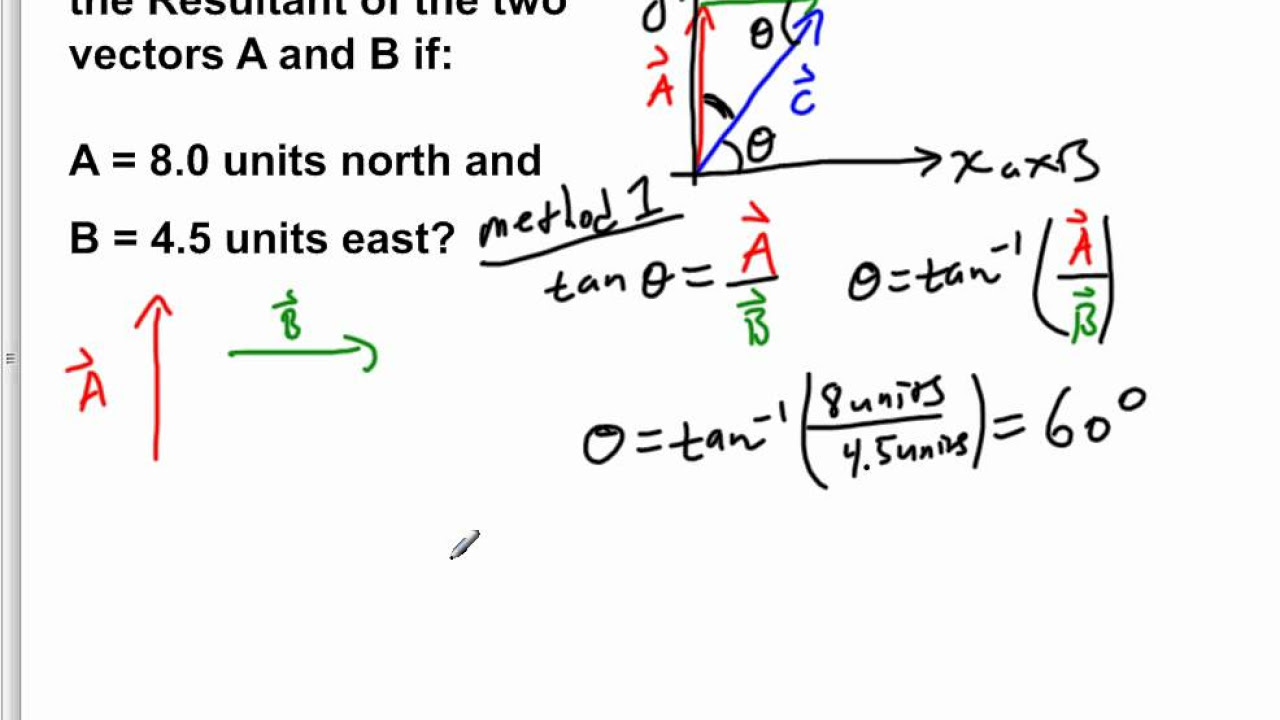
The paragraph begins with a scenario where one runs in three different directions to form a triangle: one mile north, 0.4 miles west, and 0.1 miles south. The challenge is to determine the final distance from the starting point and the angle formed with respect to the north. A coordinate system is introduced to visualize the movements, with the first leg being one mile north, the second 0.4 miles west, and the third 0.1 miles south. The paragraph emphasizes understanding how to add directional vectors and introduces the concept of resultant vectors, labeling them as a, b, and c for the three movements. The displacement north is calculated as 0.9 miles, and the displacement west is 0.4 miles, with the final step being to add these vectors to find the resultant vector r.
📏 Calculating Distance and Angle
This paragraph focuses on calculating the resultant distance r and the angle phi with respect to the north. The vertical displacement is confirmed as 0.9 miles, and the horizontal as 0.4 miles. The distance r is calculated using the Pythagorean theorem, which yields a result of approximately 1.04 or 0.98 miles. The angle phi is then determined using the cosine function and is found to be approximately 23.3 degrees. The discussion shifts to describing angles in terms of quadrants and directional bearings, emphasizing the importance of specifying the quadrant when giving an angle in relation to the cardinal directions.
🧭 Describing Angles with Directional Bearings
The final paragraph delves into the specifics of describing angles using directional bearings. It clarifies how to express angles in terms of 'degrees west of north' or 'degrees north of east'. The angle calculated earlier is described as 23.3 degrees west of north, highlighting the convention of starting with the primary direction (north) and rotating towards the secondary direction (west). The paragraph also addresses the alternative expression of the angle as 113.3 degrees, which is obtained by adding 90 degrees (for the straight line from north to east) and the 23.3 degrees. It emphasizes the importance of clarity when communicating angles on a map and the common practice of using positive and negative numbers to indicate direction relative to the north-south axis.
Mindmap
Keywords
💡coordinate system
💡vector
💡displacement
💡angle
💡trigonometry
💡hypotenuse
💡arc cosine
💡northwest
💡quadrant
💡homework problems
Highlights
The problem starts with running one mile north, 0.4 miles west, and 0.1 miles south.
A coordinate system is used to visualize the movements and calculate the final position relative to the starting point.
The first movement is one mile north, represented on the y-axis.
The second movement is 0.4 miles west, represented on the x-axis.
The third and final movement is 0.1 miles south, affecting the y-axis displacement.
The total northward displacement is calculated as 1.0 - 0.1 = 0.9 miles.
The westward displacement is 0.4 miles, as it is the only movement in that direction.
The resultant vector (r) is calculated using the Pythagorean theorem: sqrt(0.9^2 + 0.4^2).
The distance from the starting point (r) is approximately 1.04 miles.
The angle from the starting direction is calculated using trigonometric relations, specifically cosine.
The angle is found to be approximately 23.3 degrees.
The angle is described as 23.3 degrees west of north, following the convention of specifying the direction from the starting orientation.
An alternative description of the angle is 113.3 degrees, which is 90 + 23.3 degrees, following the rule of describing angles in terms of north or south of east or west.
The problem-solving process involves breaking down movements into their north-south and east-west components and then reassembling them to find the resultant displacement and direction.
The use of vectors and trigonometry is essential for calculating distances and directions in a coordinate system.
The method can be applied to various practical scenarios, such as navigation or calculating distances in a two-dimensional plane.
The importance of specifying the quadrant when describing angles in terms of north, east, south, and west is emphasized.
The concept of unit vectors is mentioned as a tool for further understanding vector addition and direction calculation.
The process of solving the problem is interactive, involving the audience in calculating and visualizing the movements.
The final position is 0.98 miles away from the starting point, with an angle of 23.3 degrees west of north.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: