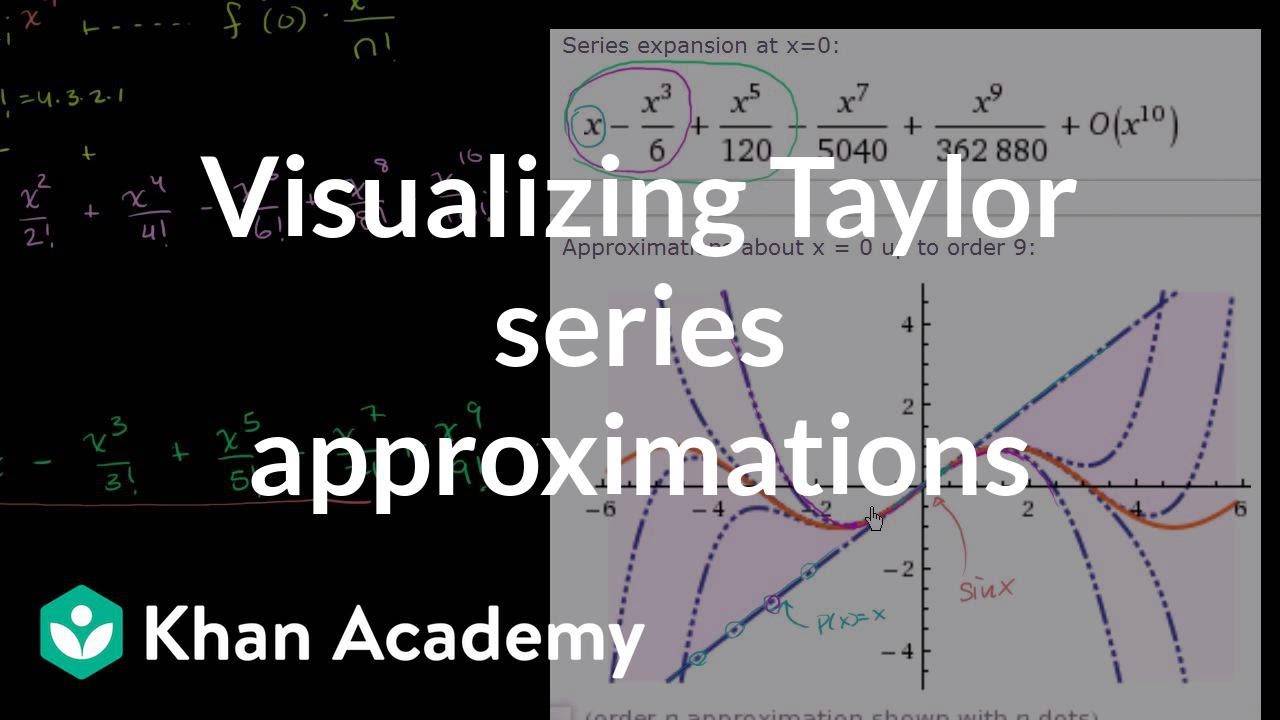
AP Calculus BC Lesson 10.14 Part 1

Elizabeth Fein

21 Mar 202331:49

EducationalLearning

32 Likes 10 Comments

TLDRThis video lesson delves into the concepts of Taylor and Maclaurin series, focusing on the accuracy of approximations as the degree of a Taylor polynomial increases. It explains how an infinite number of terms in a Taylor polynomial leads to the exact value of a function, transitioning from approximation to actual value. The video provides formulas for Taylor series and Maclaurin series, highlighting the difference between the two and emphasizing the importance of memorizing key Maclaurin series for functions like e^x, sine x, and cosine x. It also demonstrates how to derive these series through examples and tackle multiple-choice questions related to the topic.

Takeaways

📚 The concept of Taylor and Maclaurin series is introduced, with a focus on increasing the degree of Taylor polynomials for more accurate approximations of functions near a specific point.
🔍 A Taylor series becomes an exact representation of a function within its interval of convergence when an infinite number of terms are included.
🌐 The Maclaurin series is a special case of the Taylor series where the center (c) is zero, simplifying the formula for the series.
📈 Memorizing key Maclaurin series for functions like e^x, sin(x), and cos(x) is beneficial for solving calculus problems, especially in AP Calculus BC exams.
🔢 The general term formula for Maclaurin series is provided, which can be used to find the series for any function if its derivatives are known.
🌟 The process of finding the Maclaurin series for a function involves taking derivatives at the center and using the general term formula to construct the series.
📊 Examples are provided to illustrate how to find the Maclaurin series for specific functions, such as sine and cosine, and how to manipulate these series for different powers of x.
🧩 The script walks through the process of finding the first three non-zero terms and the general term for modified functions, like cosine of x cubed and 4x times e to the power of 3x.
💡 Understanding the pattern and structure of Maclaurin series is crucial for solving multiple choice questions related to this topic in calculus exams.
🔑 The script concludes with a series of multiple choice questions that test the understanding and application of the concepts of Taylor and Maclaurin series.

Q & A

What is the main topic of this video?
-The main topic of this video is Taylor and Maclaurin series, focusing on the concept of Taylor polynomials and their approximations, and how they relate to Taylor series.
What happens as the degree of a Taylor polynomial increases?
-As the degree of a Taylor polynomial increases, the approximations for the function f near x equals c (the center of the Taylor polynomial) become more accurate.
What is the difference between a Taylor polynomial and a Taylor series?
-A Taylor polynomial gives an approximation for a function at a certain value and has a finite number of terms, while a Taylor series has an infinite number of terms and can represent the exact value of the function within its interval of convergence.
What is a Maclaurin series?
-A Maclaurin series is a special case of a Taylor series where the center (c) is equal to zero. It is used to represent functions exactly within their interval of convergence.
What are the three important Maclaurin series that often appear in AP Calculus BC exams?
-The three important Maclaurin series are for e^x, sine(x), and cosine(x).
How is the Maclaurin series for e^x represented?
-The Maclaurin series for e^x is represented by 1 + x + x^2/2! + x^3/3! + x^4/4! + ..., which sums up to e^x when the series converges.
What is the general term formula for the Maclaurin series of sine(x)?
-The general term formula for the Maclaurin series of sine(x) is (-1)^n * x^(2n+1) / (2n+1)!
How does the process of finding the Maclaurin series for a function work?
-To find the Maclaurin series for a function, you take the function, differentiate it at the center (usually 0), and plug the derivatives into the Taylor series formula. The series is then summed from n=0 to infinity.
What is the Maclaurin series for the function f(x) = x + 2sin(x)?
-The Maclaurin series for f(x) = x + 2sin(x) is 2x + x^2 - 2x^3/3! + x^5/5! + ... (including the first three non-zero terms).
How can you identify the function from its Maclaurin series?
-By comparing the given Maclaurin series to known series of standard functions like e^x, sine(x), and cosine(x), and looking at the general term and pattern of the series, you can identify the function it represents.
What is the sum of the infinite series 1 - e^2 + e^4/2! - e^6/3! + e^8/4! + ...?
-The sum of the infinite series is e^(-e^2), which can be found by recognizing that the series is the Maclaurin series for e^x with x replaced by -e^2.

Outlines

00:00

📚 Introduction to Taylor and Maclaurin Series

This paragraph introduces the concept of Taylor and Maclaurin series, emphasizing the increased accuracy of approximations as the degree of a Taylor polynomial increases. It explains the transition from a finite Taylor polynomial to an infinite Taylor series, which converges to the actual function value within the interval of convergence. The paragraph also highlights the importance of understanding Taylor polynomials before delving into Taylor series and mentions the significance of memorizing three key Maclaurin series: e^x, sin(x), and cos(x).

05:03

🔢 Derivation of Maclaurin Series for Sine and Cosine Functions

The paragraph delves into the process of deriving the Maclaurin series for the sine and cosine functions. It outlines the steps for finding the derivatives of the functions at x=0 and plugging these values into the general term formula to obtain the series. The paragraph also explains how to find the Maclaurin series for more complex functions, such as cosine of x cubed and 4x times e to the power of 3x, by manipulating known series and applying distribution and simplification techniques.

10:03

📈 Constructing Power Series for Given Functions

This section focuses on constructing power series for specific functions centered at x=0, using the known Maclaurin series for sine. It demonstrates the process of distributing and simplifying terms to find the first three non-zero terms of the power series for a given function. The paragraph also addresses multiple-choice questions related to Taylor and Maclaurin series, showcasing the application of these concepts in identifying and evaluating series representations of functions.

15:04

🧩 Identifying Functions from Given Maclaurin Series

The paragraph presents a method for identifying the original function from a given Maclaurin series. It emphasizes the importance of matching the general term of the series to known functions and adjusting for any modifications, such as replacing x with x^3 or multiplying by x^2. The paragraph also provides examples of deducing functions like e to the power of x cubed and sin(x)/x from their Maclaurin series representations.

20:05

🔍 Summation of Infinite Series and Function Evaluation

This paragraph discusses the summation of infinite series and the evaluation of functions by substituting specific values into the series. It explains how to find the sum of a series by replacing the variable x with a given value, such as the natural log of 4, and how to evaluate functions like x times cosine x at pi by substituting pi into the series. The paragraph also addresses trickier questions where the series is not explicitly in terms of x, requiring the identification of the underlying function before evaluation.

Mindmap

Keywords

💡Taylor Polynomials

Taylor Polynomials are mathematical expressions used to approximate functions near a specific point, known as the center of the polynomial. In the context of the video, as the degree of a Taylor Polynomial increases, the approximation becomes more accurate. The video discusses the concept in relation to the Taylor series, emphasizing the transition from polynomials to series for improved accuracy.

💡Taylor Series

A Taylor Series is an infinite sum of terms calculated from the values of the derivatives of a function at a single point, known as the center. Unlike Taylor Polynomials, which are finite approximations, Taylor Series can represent the exact function within its interval of convergence. The video explains that the Taylor Series becomes the actual value of the function when the center is zero, which is referred to as a Maclaurin Series.

💡Maclaurin Series

A Maclaurin Series is a special case of a Taylor Series where the center is zero. It is an infinite series that provides an exact representation of a function and its derivatives at x=0. The video emphasizes the importance of memorizing certain Maclaurin Series, such as those for e^x, sin(x), and cos(x), for their frequent appearance in calculus problems.

💡Derivatives

Derivatives are mathematical concepts that represent the rate of change or slope of a function at a particular point. In the context of the video, derivatives are crucial for constructing Taylor and Maclaurin series, as they are used to determine the coefficients of the series terms.

💡Interval of Convergence

The Interval of Convergence refers to the range of values for which a Taylor or Maclaurin series converges to the function it represents. It is a critical concept because a series may not converge outside of this interval, leading to inaccurate representations of the function.

💡e^x

e^x is a common mathematical function known as the exponential function, where e is the base of the natural logarithm. In the context of the video, the Maclaurin series for e^x is given as 1 + x + x^2/2! + x^3/3! + ..., which converges to e^x for all x within its interval of convergence.

💡sin(x)

sin(x) is a trigonometric function representing the sine of an angle x in a right-angled triangle or the y-coordinate of a point on the unit circle. The video discusses the Maclaurin series for sin(x), which is a key series in calculus and trigonometry.

💡cos(x)

cos(x) is another fundamental trigonometric function that represents the cosine of an angle x in a right-angled triangle or the x-coordinate of a point on the unit circle. The video touches on the Maclaurin series for cos(x), which is crucial for understanding the behavior of cosine functions in calculus problems.

💡General Term

The General Term of a series is the formula used to express any term in the sequence without having to calculate each term individually. It provides a pattern or rule that can be applied to find any specific term in the series. In the context of the video, the General Term is used to describe the nth term of a Taylor or Maclaurin series.

💡Power Series

A Power Series is an infinite series that represents a function as the sum of terms that are powers of a variable. It is a fundamental concept in calculus used for approximating functions and solving equations. The video discusses Power Series in the context of Taylor and Maclaurin series, which are specific types of power series.

Highlights

Discussion of Taylor and Maclaurin series, emphasizing the increased accuracy of approximations as the degree of a Taylor polynomial increases.

Explanation of the Taylor series as the infinite sum of terms from the Taylor polynomial, which converges to the actual function value within the interval of convergence.

Formula for the general term of a Taylor polynomial and how it differs from the Taylor series, particularly noting the infinite summation and the value of the function rather than an approximation.

Introduction to the Maclaurin series as a special case of the Taylor series where the center is zero, and its equivalence to the Taylor polynomial when centered at x=0.

Three important Maclaurin series to memorize for AP Calculus BC exams: e^x, sin(x), and cos(x), with their respective general term formulas.

Derivation of the Maclaurin series for sine(x) by finding derivatives at x=0 and plugging them into the general term formula.

Explanation of how to find the Maclaurin series for functions like cosine(x^3) by replacing x with x^3 in the known series of cosine(x).

Process of finding the Maclaurin series for a given function f(x) = x + 2sin(x) by distributing the binomial (x + 2) across the series for sin(x).

Solution to multiple-choice questions involving identifying the function from its Maclaurin series, such as recognizing the series for e^(x^3) and sin(x/x).

Methodology for determining the original function from a given infinite series by matching general terms and substituting specific values for x.

Example of summing an infinite series by replacing non-x terms with x and evaluating the function at the given value, as demonstrated with e^(x) and ln(4).

Explanation of how the Maclaurin series for cosine(x) can be manipulated to find the series for x*cos(x) by multiplying the general term by x.

Strategy for solving multiple-choice questions that involve identifying the function from a series by comparing general terms and evaluating the function at specific values.

Illustration of the power series convergence to specific functions by identifying patterns in the series and matching them to known functions like e^(x) and sin(x).

Demonstration of the process for finding the sum of an infinite series by substituting a value into the base function, as shown with e^(x) and -e^2.

Application of the Maclaurin series to solve problems involving infinite series and their sums, showcasing the practical use of the series in calculus.

Explanation of how to work with Maclaurin series when the variable is not explicitly x, such as when the series is given in terms of e^2 or pi.

Overview of the process for finding the Maclaurin series for composite functions like 4x*e^(3x) by substituting and distributing known series terms.

Discussion of the importance of memorizing key Maclaurin series for efficiency in solving calculus problems, particularly for exams like AP Calculus BC.

Transcripts

Browse More Related Video

AP Calculus BC Lesson 10.11 Part 1

Maclaurin series of cos(x) | Series | AP Calculus BC | Khan Academy

Calculus BC – 10.14 Finding Taylor or Maclaurin Series for a Function

Taylor Polynomials Day 1

Visualizing Taylor series approximations | Series | AP Calculus BC | Khan Academy

Finding Taylor Series

Related Tags

Mathematics Calculus Taylor Series Maclaurin Series Infinite Series e^x Trigonometric Functions Series Approximations Function Values Math Tutorial