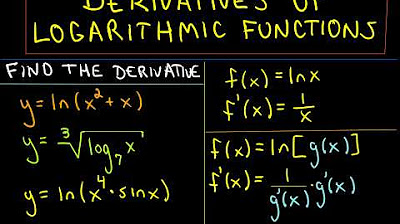Math1325 Lecture 11 1 Derivatives of Logarithm
TLDRThis transcript is a comprehensive lecture on derivatives of logarithmic functions, a topic that may be new to many students. The lecture begins by reviewing the concept of logarithms as the inverse operation to exponentiation, explaining the components of an exponential equation and how it translates into a logarithmic form. It then delves into the properties of logarithms, such as the common logarithm (base 10) and the natural logarithm (base e), and the rules for manipulating logarithms, including the product rule, quotient rule, and power rule. The focus then shifts to the derivatives of logarithmic functions, illustrating how the derivative of the natural logarithm function is 1/x, and how to apply the chain rule when differentiating composite functions involving logarithms. The lecture provides several examples to demonstrate the process of finding derivatives of logarithmic functions, including handling more complex expressions involving products, quotients, and powers. The summary concludes with a reminder of the derivative of a logarithm with a general base 'a', emphasizing that 'a' is a constant and thus can be factored out of the derivative.
Takeaways
- 📚 Logarithms are the inverse operation to exponentiation, similar to how subtraction is the inverse of addition and multiplication is the inverse of division.
- 🔢 In an exponential equation, you have a base, an exponent, and an answer, while in a logarithmic equation, the base and the answer swap places, and you solve for the exponent.
- 📈 The common logarithm (base 10) is often denoted without a base, whereas the natural logarithm (base e) is denoted as ln(x).
- ✅ Three key properties of logarithms include: the product rule (log(a*b) = log(a) + log(b)), the quotient rule (log(a/b) = log(a) - log(b)), and the power rule (log(a^b) = b*log(a)).
- 📈 For the natural logarithm function, the value of x at any point corresponds to the slope of the tangent line at that point on its graph.
- 🧮 The derivative of the natural logarithm function ln(x) is given by the formula 1/x, which is a shortcut useful for calculations.
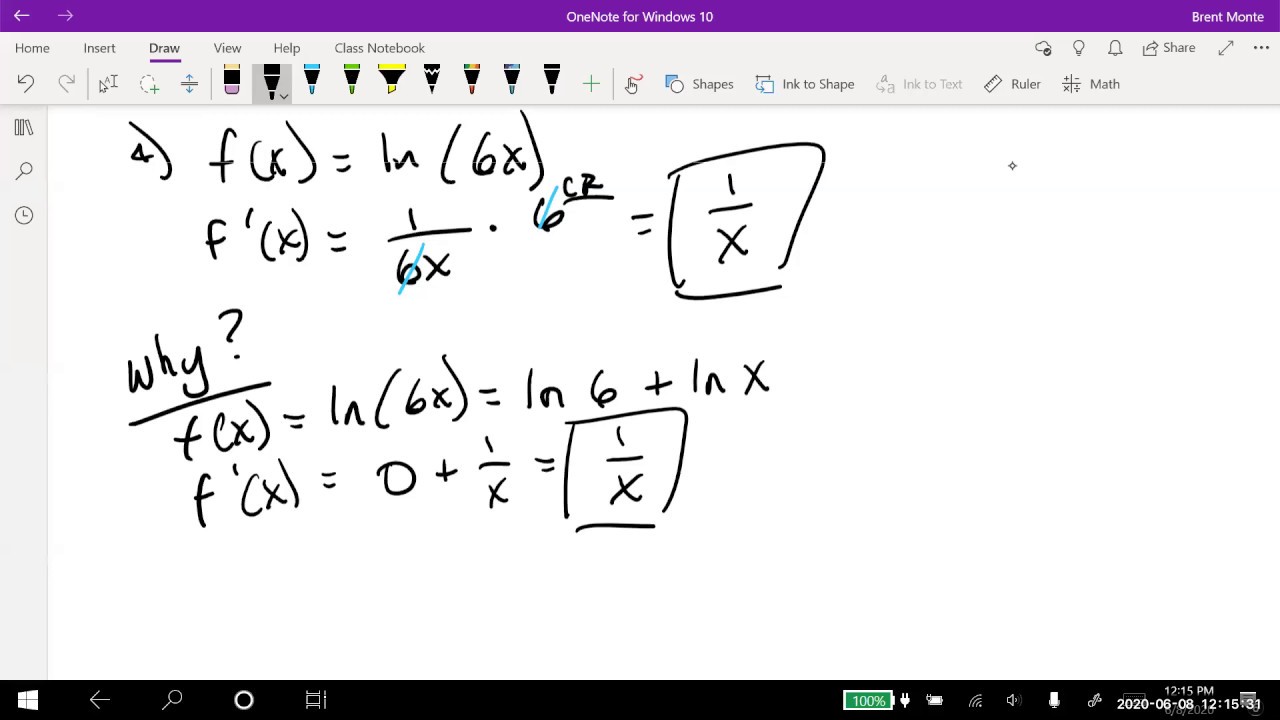
- 📌 When differentiating a constant times a function, such as 3 * ln(x), the derivative is the constant times the derivative of the function, resulting in 3/x.
- 🤔 The product rule for derivatives states that the derivative of a product of two functions is the derivative of the first times the second plus the first times the derivative of the second.
- 🔄 The chain rule is applied when differentiating a composition of functions, such as ln(x^4 - 3x + 7), resulting in (1/(x^4 - 3x + 7)) * (4x - 3).
- ✅ Simplifying the argument of a logarithm before differentiating can make the process easier, as shown when breaking down ln(x * x^5 - 2^10) into separate logarithms and applying the power rule.
- 💡 The derivative of a logarithm with a general base 'a' is given by the formula 1/(x * ln(a)), pulling out the constant 'a' as it does not change with differentiation.
Q & A
What is the relationship between exponents and logarithms in mathematics?
-Exponents and logarithms are inverse operations. While exponents are used to express what power a base must be raised to in order to produce a given number, logarithms are used to find the power to which the base must be raised to obtain a given number, effectively 'undoing' the exponentiation.
What is a common logarithm and how is it denoted?
-A common logarithm is a logarithm with a base of 10. It is often denoted as 'log' without specifying the base, as the base 10 is the most commonly used in many mathematical contexts.
What is the natural logarithm and how is it represented?
-The natural logarithm is a logarithm with a base of Euler's number, which is a mathematical constant approximately equal to 2.71828. It is represented as 'ln', which stands for 'natural log'.
What are the three properties of logarithms that allow us to manipulate them?
-The three properties are: 1) The log of a product equals the sum of the logs of the factors (log(a*b) = log(a) + log(b)). 2) The log of a quotient equals the difference of the logs of the numerator and denominator (log(a/b) = log(a) - log(b)). 3) The log of a number raised to a power equals the power times the log of the number (log(a^b) = b * log(a)).
How is the derivative of the natural logarithm function expressed?
-The derivative of the natural logarithm function, ln(x), is expressed as 1/x. This is a shortcut formula that is useful for finding the derivative of functions involving natural logarithms.
What is the process to find the derivative of a function that is a product of two other functions?
-To find the derivative of a product of two functions, you use the product rule, which states that the derivative of the first times the second plus the derivative of the second times the first. Mathematically, it is expressed as (f(x) * g(x))' = f'(x) * g(x) + f(x) * g'(x).
What is the chain rule in calculus, and how is it applied when finding the derivative of a function that is a composition of two other functions?
-The chain rule is a method for finding the derivative of a composition of functions. It states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, times the derivative of the inner function. It is expressed as (f(g(x)))' = f'(g(x)) * g'(x).
What is the derivative of the function f(x) = 3x^2 + 3ln(x)?
-The derivative of the function f(x) = 3x^2 + 3ln(x) is found by applying the power rule to the first term and the derivative of the natural logarithm to the second term. The result is 6x + 3/x.
How can you simplify the expression ln(x(x^5 - 2^10)) using logarithm properties?
-The expression can be simplified by using the property of logarithms that allows us to split the log of a product into the sum of logs. It becomes ln(x) + ln(x^5 - 2^10), which further simplifies to ln(x) + 5ln(x) - 10ln(2), and then to ln(x) + 50x^4/(x^5 - 2^10).
What is the derivative of the function f(x) = ln((x^3 + 1)/ln(4))?
-The derivative of the function f(x) = ln((x^3 + 1)/ln(4)) is found by applying the quotient rule and the chain rule. It results in (3x^2)/(x^3 + 1) times (1)/(ln(4)).
How do you find the derivative of a logarithmic function with a base other than 'e' or '10'?
-To find the derivative of a logarithmic function with a base 'a' (where a is a constant), you use the change of base formula to convert it to a natural logarithm, and then apply the derivative as 1/x times the derivative of the argument of the logarithm. The derivative of log_a(x) is (1/(ln(a) * x)).
Outlines
📚 Introduction to Derivatives of Logarithmic Functions
The first paragraph introduces the concept of logarithms as the inverse operation to exponentiation. It explains the structure of an exponential equation and how it can be rewritten as a logarithm, emphasizing that logarithms solve for the exponent. The paragraph also discusses the common logarithm (base 10) and the natural logarithm (base e), denoted as ln. It covers three fundamental properties of logarithms: the product rule, quotient rule, and power rule. The paragraph concludes with an example of the derivative of the natural logarithm function, which is found to be 1/x, and touches on the chain rule for derivatives of composite functions.
🔢 Derivatives of Logarithmic Functions: Examples and Techniques
The second paragraph delves into examples of finding derivatives of logarithmic functions. It begins with a straightforward application of the power rule to find the derivative of 3x squared plus three times the natural log of x. The explanation then moves on to the product rule and chain rule, illustrating how to find derivatives of more complex logarithmic expressions, such as the natural log of a quotient or a function composed with another function. The paragraph also simplifies expressions using logarithmic properties, such as separating the log of a product into the sum of individual logarithms and applying the power rule to logarithms. It concludes with a discussion on the derivative of a logarithm with a variable base, emphasizing the importance of treating the base as a constant when differentiating.
📝 Advanced Derivatives of Logarithms and Composite Functions
The third paragraph continues the exploration of derivatives of logarithmic functions, focusing on more complex scenarios involving composite functions. It demonstrates the use of the chain rule to find the derivative of the natural log of a function, such as x to the fourth power minus 3x plus 7. The paragraph also shows how to simplify the derivative by first simplifying the argument of the logarithm. It concludes with an example involving the derivative of a logarithm with a base other than e or 10, highlighting the technique of factoring out constants and differentiating the remaining function.
Mindmap
Keywords
💡Logarithm
💡Exponential Equation
💡Derivative
💡Natural Log (Ln)
💡Product Rule
💡Quotient Rule
💡Chain Rule
💡Power Rule
💡Constant
💡Base
Highlights
Logarithms are the inverse operation to exponentiation, allowing us to solve for the exponent in an exponential equation.
The common logarithm (base 10) and natural logarithm (base e) are two special types of logarithms.
Three key properties of logarithms: product rule, quotient rule, and power rule, are essential for manipulation.
The derivative of the natural logarithm function, f(x) = ln(x), is 1/x.
When differentiating a function involving a constant times a logarithm, the constant remains outside and is multiplied by the derivative of the logarithm.
The product rule is applied when differentiating a product of two functions, involving multiplying the derivatives of each function.
The quotient rule is used to differentiate a quotient of two functions, involving the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all over the square of the denominator.
The chain rule is applied when differentiating a composition of functions, involving the derivative of the outer function times the derivative of the inner function.
The derivative of a logarithm with a base other than e or 10 is derived by using the change of base formula.
The derivative of a logarithmic function can be simplified by first simplifying the argument of the logarithm.
The derivative of ln(x) involves multiplying 1/x by the derivative of the function inside the logarithm.
The power rule for logarithms allows us to bring down the power as a coefficient in front of the logarithm.
The derivative of a logarithmic function can be found by applying the logarithmic properties and rules, such as the product and power rules.
The derivative of a complex logarithmic expression can be simplified by breaking it down into its components and applying the appropriate differentiation rules.
Constants within logarithmic expressions can be factored out of the derivative, as they do not change the derivative of the function.
The derivative of a logarithmic function involving a quotient can be simplified by applying the quotient rule and then simplifying the resulting expression.
The process of differentiating logarithmic functions involves a combination of algebraic manipulation and application of differentiation rules.
Understanding the relationship between the value of x and the slope of the tangent at that point is crucial for visualizing the derivative of a logarithmic function.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: