Linear Programming - GCE 2023 Paper 1

Roadmap Tuition Centre
12 Oct 202308:02
EducationalLearning
32 Likes 10 Comments

TLDRThis video script explains how to define inequalities for an unshaded region in a diagram. The process involves identifying key lines, determining if they are solid or dotted to ascertain whether the equal sign is included, and using coordinates to derive the equations of the lines. The script demonstrates how to find the equation of a line by using two points and the slope-intercept form, and then translates these into inequalities that describe the unshaded area. Three specific inequalities are derived, each corresponding to a different line in the diagram, with careful attention to whether the line includes the boundary or not.

Takeaways
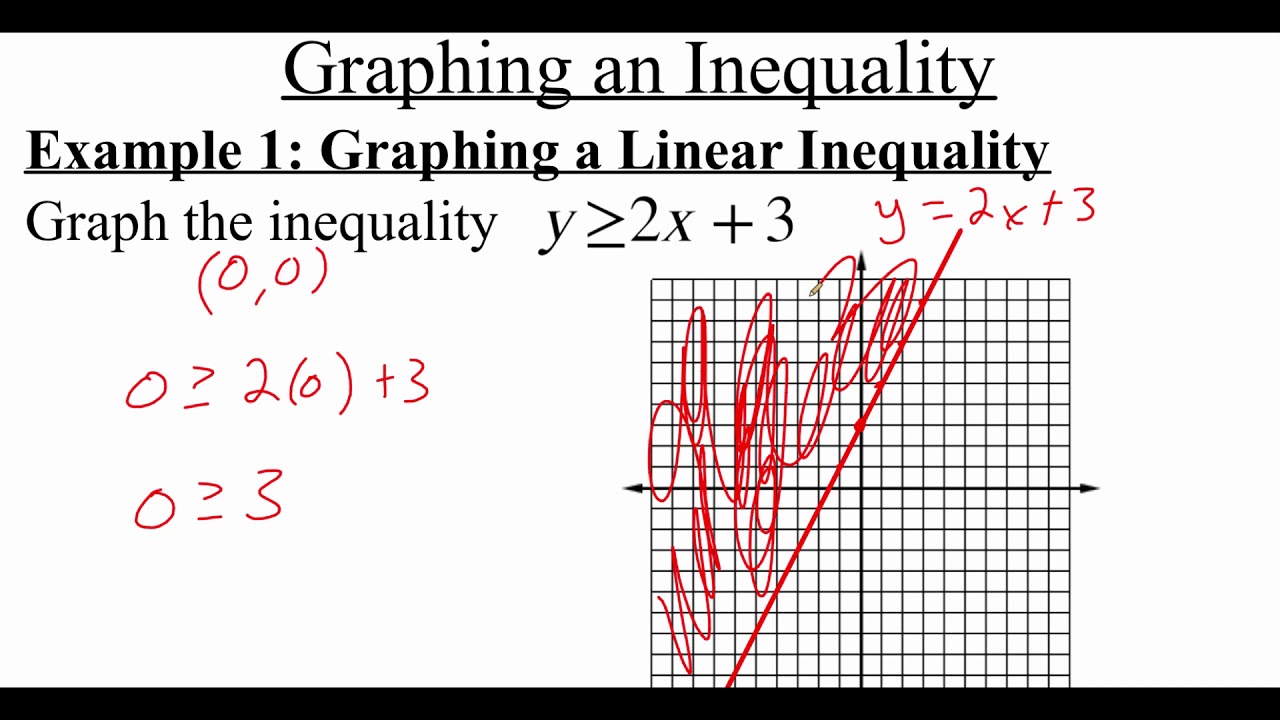
  • 📏 The first inequality defines a line parallel to the x-axis, cutting the y-axis at 1, resulting in the condition Y = 1.
  • 🔍 For the second inequality, the line is identified by choosing two points on it, and the equation is derived using the slope-intercept form.
  • 📉 The second line is determined to be solid, not broken, which means the inequality includes the 'equal to' condition, leading to Y ≥ 1.
  • 📚 The equation of the second line is found by setting up a proportion using the coordinates of two points and solving for Y in terms of X, resulting in Y = X + 6.
  • 🚫 The unshaded region for the second line indicates that the inequality should be Y ≤ X + 6, as the greater part is shaded.
  • 📐 The third inequality involves finding the equation of a line using the origin (0,0) and another point (2,4), leading to the equation Y = 2X.
  • 🛑 The third line is dotted, indicating that the inequality should not include 'equal to', resulting in Y < 2X.
  • 🔑 The process emphasizes the importance of identifying whether a line is solid or broken to correctly set up the inequality.
  • 📈 The method for finding the equation of a line involves using two points and the slope formula, which is crucial for defining inequalities.
  • 📝 The final result is three inequalities that define the unshaded region in the diagram: Y = 1, Y ≤ X + 6, and Y < 2X.
  • 📋 The transcript provides a step-by-step guide on how to derive inequalities from a diagram, highlighting the importance of line characteristics and coordinates.
Q & A

  • What is the first inequality mentioned in the script, and how is it derived?

    -The first inequality mentioned is Y = 1, which is derived from observing that the line cuts the Y-axis at one. This is a straightforward observation since any line parallel to the X or Y-axis that intersects the axis will give a constant value of the axis it intersects.

  • Why is it important to determine if a line is dotted or solid when defining inequalities?

    -The importance of determining if a line is dotted or solid lies in how the inequality is defined. A solid line typically includes the points on the line itself, leading to an inequality like 'greater than or equal to'. A dotted line, on the other hand, indicates that the line itself is not included, resulting in an inequality like 'greater than'.

  • How does one find the equation of a line given two points?

    -To find the equation of a line given two points (x1, y1) and (x2, y2), one can use the formula (y - y1) / (y2 - y1) = (x - x1) / (x2 - x1). This formula is derived from the slope-intercept form of a line, y = mx + b, where m is the slope and b is the y-intercept.

  • What is the second inequality derived from the script, and what is its significance?

    -The second inequality is y ≤ x + 6. It is derived from the equation y = x + 6, which represents a line that the unshaded region is below. The significance of this inequality is that it defines the boundary of the unshaded region for the part of the line that is not shaded.

  • What does the script suggest about the line with the equation y = 2x?

    -The script suggests that the line y = 2x is a boundary for the unshaded region, with the inequality y < 2x. This indicates that the unshaded region lies below this line, and the line itself is dotted, meaning it is not included in the unshaded region.

  • How does the script handle the inclusion of the Y-axis when defining the first inequality?

    -The script simply states that the line cuts the Y-axis at one, leading to the inequality Y = 1. This is a direct observation without the need for calculation, as the line is parallel to the X-axis.

  • What is the method used in the script to find the equation of the second line?

    -The method used is to pick two points along the line, calculate the slope using the formula (y2 - y1) / (x2 - x1), and then use the slope and one of the points to find the equation of the line in the slope-intercept form y = mx + b.

  • How does the script determine whether to include 'equal to' in the inequalities?

    -The script determines whether to include 'equal to' based on whether the line is solid or dotted. A solid line includes the points on the line itself, so 'equal to' is included in the inequality. A dotted line does not include the line itself, so 'equal to' is not included.

  • What is the third inequality mentioned in the script?

    -The third inequality mentioned is y < 2x, which is derived from the line y = 2x. The unshaded region is below this line, and since the line is dotted, the inequality does not include 'equal to'.

  • What is the process for deriving the equation of the third line from the script?

    -The process involves picking two points that the line passes through, such as the origin (0,0) and another point like (2,4). Then, using the formula for the slope and the points, the equation y = 2x is derived.

  • How does the script ensure that the derived inequalities accurately represent the unshaded region?

    -The script ensures accuracy by carefully observing which part of the line is shaded and which is not, and by considering whether the lines are solid or dotted. This observation directly informs the direction of the inequality signs.

Outlines
00:00
📚 Analyzing Inequalities and Equations in a Diagram

This paragraph discusses the process of defining inequalities and deriving equations from a diagram. The speaker starts by identifying the first inequality, which is a horizontal line cutting the Y-axis at 1, simplifying to Y=1. They then consider the inequality aspect, noting that the shaded region implies Y should be greater than one, and whether the line is dotted or solid to determine if the inequality should include equality. Moving to the second inequality, the speaker picks coordinates along the line and uses the slope formula to derive the equation Y = X + 2. For the third inequality, the origin and another point are used to find the equation Y = 2X, and the inequality is set as Y less than 2X due to the broken line indicating the shaded region.

05:00
📐 Deriving Line Equations and Inequalities from a Graph

The second paragraph continues the discussion on deriving equations and inequalities from a graph. The speaker identifies the second line, noting that the shaded region indicates the greater part, leading to the inequality Y less than or equal to X + 6 due to the solid line. For the third line, the origin and another point are selected to find the equation Y = 2X. The inequality is Y less than 2X, as the line is broken, indicating that the equality is not included. The speaker summarizes the three inequalities needed for the question, marking the end of the explanation.

Mindmap
Keywords
💡Inequality
In mathematics, an inequality is a relation that holds between two expressions if one is greater than, less than, greater than or equal to, or less than or equal to the other. In the context of the video, inequalities are used to define the boundaries of a region in a coordinate plane. For example, the transcript mentions 'Y is greater than one' to describe the area above a certain line on the Y-axis.
💡Unshaded region
The unshaded region in the video refers to the area of the coordinate plane that is not shaded or filled in, which is defined by certain inequalities. It is the area that the inequalities are describing. The transcript discusses defining inequalities for this region, such as 'Y is greater than one' and 'Y is less than or equal to X + 6'.
💡Y-axis
The Y-axis is a fundamental part of the Cartesian coordinate system, representing the vertical axis. In the video, the Y-axis is mentioned when discussing where a line cuts the axis, such as 'this line here it's cutting the Y-axis at one', which helps in defining the inequalities.
💡Line
In the context of the video, a line refers to a straight one-dimensional figure in the coordinate plane that can be defined by an equation. The script discusses various lines, such as 'this line that we have labeled one', and how they are used to define the unshaded region through inequalities.
💡Dotted line
A dotted line in the video script is used to indicate a boundary that does not include the points on the line itself. This is contrasted with a solid line, which may include the points on the line. For instance, the transcript states 'if it is then the answer becomes the way I've written it which is, y is greater than one', indicating that the inequality does not include the line itself.
💡Solid line
A solid line, as mentioned in the script, is a continuous line that may include the points on the line when defining an inequality. For example, the transcript says 'if the line is not a broken line that means we also include the equal to', which means the inequality includes the points on the line.
💡Coordinates
Coordinates are pairs of numbers that define a point's position in a coordinate system. In the video, specific coordinates like '2 comma 4' and '5 comma 1' are used to find the equation of a line. These points help in determining the slope and y-intercept of the line, which are essential for writing its equation.
💡Slope
The slope of a line in a coordinate plane is a measure of its steepness, calculated as the change in the y-coordinate divided by the change in the x-coordinate between two points on the line. The script uses the concept of slope when finding the equation of a line, as seen when calculating 'y1 over Y 2 - y1 is equal to x - X1 / X2 - X1'.
💡Y-intercept
The y-intercept is the point where a line crosses the Y-axis. It is a key part of the line's equation and is represented as 'b' in the equation y = mx + b, where 'm' is the slope. The video script mentions finding the y-intercept when discussing the equation 'Y is equal to X + 6'.
💡Cross multiply
Cross multiplying is a method used in algebra to solve proportions or to clear fractions when solving equations. In the script, this method is used when finding the equation of a line, as indicated by 'cross multiply where we shall now say that three there it is multiplying y - 4, being equal to 3 there, multiplying the x - 2'.
Highlights

Identifying the unshaded region in the diagram requires defining three inequalities.

The first inequality is straightforward as the line cuts the y-axis at 1, so y = 1.

For the second inequality, consider if the line is dotted or solid to determine if y is greater than or equal to 1.

To find the equation of the second line, pick two points (2,4) and (5,1) and use the formula y1/y2 - y1 = x - x1 / x2 - x1.

Simplify the equation to y = x + 2 + 4 = x + 6 for the second line.

The inequality for the second line is y ≤ x + 6 since the greater part is shaded and the line is solid.

For the third line, pick the origin (0,0) and point (2,4) to find its equation.

The equation of the third line is y = 2x after simplifying.

The inequality for the third line is y < 2x as the greater part is shaded and the line is dotted.

The three inequalities needed to define the unshaded region are y = 1, y ≤ x + 6, and y < 2x.

Lines parallel to the axes can be easily identified by their intercepts.

Consider if a line is dotted or solid when determining inequalities.

Use two points on a line to find its equation using the formula y1/y2 - y1 = x - x1 / x2 - x1.

Simplify the equation by cross-multiplying and isolating y.

Determine if the inequality should include equality based on if the line is solid or dotted.

The unshaded region is defined by the inequalities y = 1, y ≤ x + 6, and y < 2x.

This method can be applied to any diagram with linear inequalities to define regions.

Transcripts

Browse More Related Video

7.4.1 Graphing an Inequality

Solving Algebraic Inequalities

Graphing Lines in Slope-Intercept Form (y = mx + b)

Inequalities with Rational Functions (Precalculus - College Algebra 47)

Solving Polynomial Inequalities

Graphing Lines in Algebra: Understanding Slopes and Y-Intercepts

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
InequalitiesMathematicsTutorialDiagramY-axisX-axisEquationsShaded RegionLine AnalysisEducational