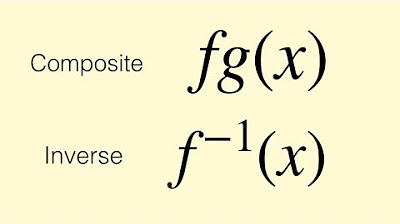10 - What are Composite Functions? (Part 1) - Evaluating Composition of Functions & Examples
TLDRThis video lesson introduces composite functions, a fundamental concept in calculus that often confuses students. The instructor simplifies the idea by comparing functions to mathematical 'black boxes' that process inputs. The script explains how to chain functions, such as f(x) and g(x), to create a composite function, which is calculated by passing the output of one function into another. The instructor uses examples like f(x) = x squared and g(x) = 2x to demonstrate the process and emphasizes the importance of order in composite functions, noting that f(g(x)) is not equivalent to g(f(x)). The lesson builds a foundation for understanding inverse functions and their applications in higher mathematics.
Takeaways
- 📚 The lesson introduces composite functions, emphasizing their importance in understanding more complex calculus problems.
- 🔍 A function is likened to a 'black box' that takes an input, performs a calculation, and produces an output, which can be visualized graphically.
- 🔗 Composite functions are created by chaining two separate functions together, where the output of one function becomes the input of another.
- 📐 The concept of order of operations is highlighted, stressing the need to evaluate the innermost function first before moving outwards.
- 📝 The notation for composite functions is explained, with an example of \( f(g(x)) \), which means to evaluate \( g(x) \) first and then apply \( f \) to the result.
- 🔢 Simple examples are used to illustrate composite functions, such as \( g(x) = 2x \) and \( f(x) = x^2 \), to demonstrate the process of linking functions.
- 📉 The script provides step-by-step calculations to show how to find the value of a composite function for specific inputs and in a more general form.
- 🚫 It clarifies that composite functions are not commutative, meaning \( f(g(x)) \) is not necessarily equal to \( g(f(x)) \).
- 🔄 The lesson includes practice problems to reinforce the concept, such as finding \( f(g(4)) \) and \( g(f(4)) \) with given functions.
- 📚 The importance of understanding composite functions is emphasized as a foundation for more advanced topics like inverse functions and logarithms.
- 🔑 The script hints at an upcoming lesson on inverse functions, which are a special case where the order of composition may not matter.
Q & A
What is a composite function?
-A composite function is a function that is formed by applying one function to the result of another function. It is like a combination of two functions where the output of the first function becomes the input of the second function.
Why are composite functions important in calculus?
-Composite functions are important in calculus because they are extensively used in solving more complex problems. Understanding composite functions is fundamental to performing various operations in calculus.
What is the general representation of a composite function?
-The general representation of a composite function is f(g(x)), which means you first evaluate the function g at x, and then evaluate the function f at the result of g(x).
What is the graphical interpretation of a composite function?
-Graphically, a composite function involves taking input values, calculating the output of the first function (G(x)), and then using that output as the input for the second function (F(x)). The final output is then plotted, showing the relationship between the input and the composite function's result.
Can you provide a simple example of a composite function from the script?
-Yes, a simple example given in the script is G(x) = 2x and F(x) = x^2. The composite function would be F(G(x)) = F(2x) = (2x)^2 = 4x^2.
How do you calculate F(G(x)) if G(x) = 2x and F(x) = x^2?
-To calculate F(G(x)), you first evaluate G(x) which is 2x, and then you substitute this result into F(x). So, F(G(x)) = F(2x) = (2x)^2 = 4x^2.
What is the difference between F(G(x)) and G(F(x))?
-F(G(x)) and G(F(x)) represent two different composite functions. F(G(x)) means you first apply the function G to x and then apply F to the result. Conversely, G(F(x)) means you first apply the function F to x and then apply G to the result. In general, F(G(x)) is not equal to G(F(x)) unless the functions are inverses of each other.
Why might students get confused with composite functions?
-Students might get confused with composite functions due to the nested or chained nature of the functions, which requires understanding the order of operations and working from the inside out. The notation can also be misleading, as it looks complex with multiple functions involved.
What is the significance of the order of operations in composite functions?
-The order of operations is crucial in composite functions because it dictates which function to evaluate first. You must evaluate the innermost function (the one on the rightmost side of the parentheses) before the outer function, similar to how you would evaluate expressions within nested parentheses.
What is the relationship between composite functions and inverse functions?
-Composite functions lay the groundwork for understanding inverse functions. Inverse functions are a special case where the order of composition does not matter, and the result of f(g(x)) is the same as g(f(x)). This is due to the properties of inverse functions where one function 'undoes' the other.
How can practicing with composite functions help in understanding calculus better?
-Practicing with composite functions helps in understanding the foundational concepts that are essential for more advanced topics in calculus, such as inverse functions and logarithms. It builds the necessary skills to handle complex problems and operations within calculus.
Outlines
📚 Introduction to Composite Functions
The script introduces the concept of composite functions, emphasizing their simplicity despite students' common confusion. It explains functions as 'black boxes' that perform calculations, taking inputs (X values) and producing outputs (f(X)). The composite function is then defined as the chaining of two distinct functions, f(X) and g(X), where the output of one becomes the input of the other. The script uses the example of f(X) = X squared and g(X) = 2X to illustrate how composite functions work, highlighting the importance of understanding composite functions in calculus.
🔗 Understanding Composite Functions as 'Chained' or 'Nested'
This paragraph delves deeper into composite functions, likening them to 'chained' or 'nested' operations, which must be performed from the inside out, akin to order of operations in mathematics. It provides a concrete example using the functions g(X) = 2X and f(X) = X squared, demonstrating how to calculate f(g(X)) by first evaluating g(X) and then plugging the result into f(X). The paragraph clarifies that composite functions can involve more than two functions and emphasizes the importance of correctly applying the order of operations.
📘 Practical Calculations with Composite Functions
The script moves on to practical calculations, using specific numerical examples to illustrate the process of evaluating composite functions. It demonstrates how to calculate f(g(2)) and f(g(3)) using the previously defined functions, leading to the general formula f(g(X)) = 4X squared. The paragraph reinforces the concept by showing that composite functions create a 'new' function that is a product of the original two functions, possessing characteristics of both.
🔍 Exploring the Distinctions Between Composite Functions
This section addresses the misconception that reversing the order of composite functions yields the same result, clearly stating that f(g(X)) is not equal to g(f(X)) in general. It provides an example with new functions f(X) = 3X - 5 and g(X) = the square root of X, calculating both f(g(4)) and g(f(4)) to show that they produce different outcomes. The paragraph also introduces the concept of inverse functions as a special exception where the order of composition may not matter, setting the stage for further lessons.
📘 General Expressions and the Importance of Composite Functions
The final paragraph wraps up the discussion by generalizing the process of calculating composite functions with variables rather than specific numbers. It shows how to derive the expressions for f(g(X)) and g(f(X)) using the general form of X, resulting in different outcomes that highlight the importance of order in composite functions. The script concludes by emphasizing the foundational role of composite functions in understanding more advanced mathematical concepts such as inverse functions and logarithms.
Mindmap
Keywords
💡Composite Functions
💡Function
💡Input and Output
💡Nested Functions
💡Chained Functions
💡Order of Operations
💡Graph
💡Algebra and Precalculus
💡Calculus
💡Inverse Functions
Highlights
Introduction to composite functions, emphasizing their importance in calculus.
Explanation of a function as a 'black box' with inputs and outputs.
Composite functions are created by chaining two separate functions together.
The concept of reading composite functions from 'inside to outside'.
Graphical representation of composite functions as a combination of two functions.
Simple example using functions G(x) = 2x and f(x) = x^2 to illustrate composite functions.
Calculating composite functions with specific numerical examples.
Generalizing the process of composite functions with variable x.
Result of a composite function is a new function that has characteristics of both original functions.
Differentiating between composite functions and regular mathematical operations like addition and multiplication.
Demonstration of calculating F(G(x)) and G(F(x)) with given functions f(x) = 3x - 5 and g(x) = √x.
Clarification that F(G(x)) is not necessarily equal to G(F(x)) for composite functions.
The importance of order in composite functions and its difference from basic arithmetic.
Introduction of the concept of inverse functions as a special case where the order may not matter.
The foundational role of composite functions in understanding more advanced mathematical concepts.
Encouragement for students to practice composite functions to solidify their understanding.
Anticipation of the next lesson focusing on inverse functions and their significance in mathematics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: