Calculating amplitude, frequency,wavelength and period of a wave
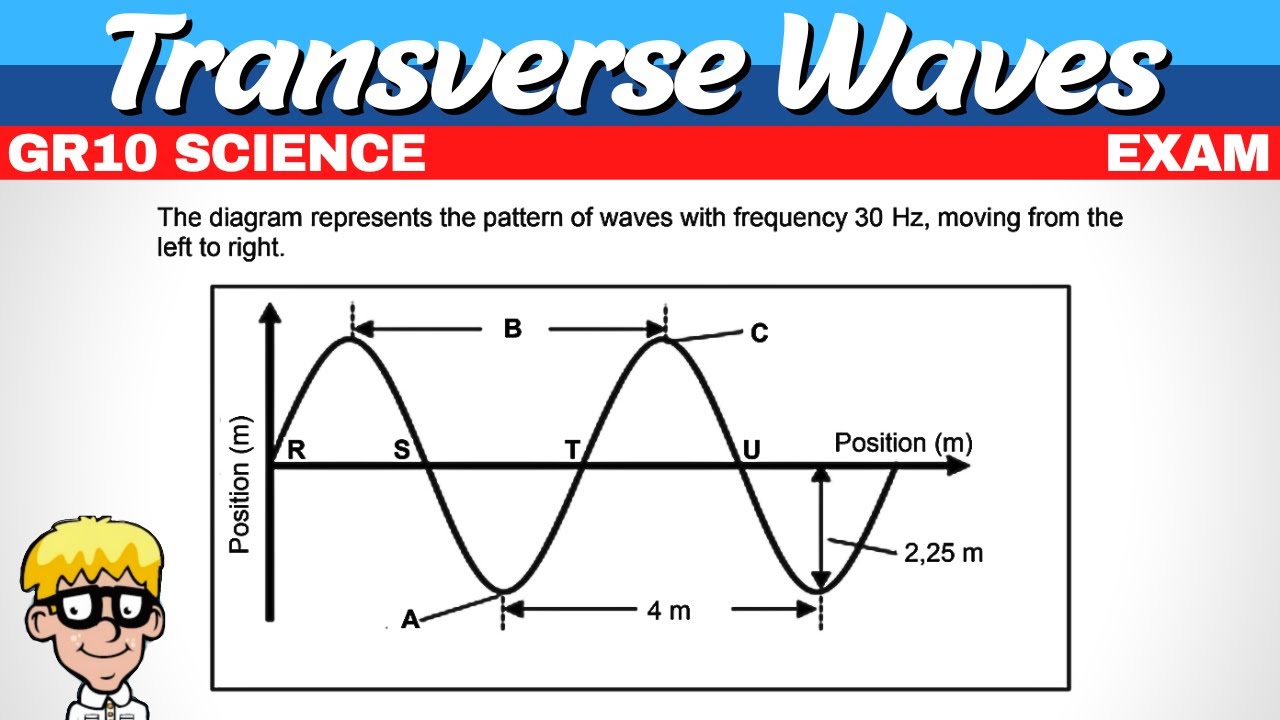
TLDRThe script explains how to determine the physical properties of a wave from a snapshot diagram, including wavelength, amplitude, frequency, and period. It clarifies that wavelength is the distance for one oscillation, found to be 40 cm or 0.4 m in the example. Amplitude, the maximum displacement from equilibrium, is identified as 5 cm or 0.05 m. Frequency is calculated using the formula speed divided by wavelength, resulting in 25 Hz. Lastly, the period is the reciprocal of frequency, calculated to be 0.04 seconds, providing a simple yet comprehensive understanding of wave properties.
Takeaways
- 📏 Wavelength is the distance covered by a wave when it completes one oscillation.
- 🌊 Wavelength can be determined from a displacement versus distance graph by measuring the distance between two successive crests or troughs.
- 📐 In the given example, the wavelength is 40 centimeters (0.4 meters).
- 📈 Amplitude is the maximum displacement of a particle from its equilibrium position.
- 🖐 The amplitude of the wave in the example is 5 centimeters (0.05 meters).
- 🔄 Frequency is the number of oscillations per unit time and can be calculated using the wave speed and wavelength.
- ⚡ In the example, the frequency is calculated as 25 Hz.
- ⏲ Period of oscillation (T) is the reciprocal of the frequency.
- 🔄 The period of the wave in the example is 0.04 seconds.
- 📝 The script demonstrates how to calculate wavelength, amplitude, frequency, and period of a wave using given data and formulas.
Q & A
What does Figure 8.19 in the example represent?
-Figure 8.19 shows a snapshot of a waveform in a stream, with numbers indicating the scale in centimeters.
What is the speed of the wave in the example?
-The speed of the wave is 10 meters per second.
How can the wavelength be determined from the diagram?
-The wavelength can be determined by measuring the distance between two consecutive troughs or crests in the displacement versus distance diagram. For instance, the distance from one trough to the next is 40 centimeters.
What is the wavelength of the wave in the given example?
-The wavelength of the wave is 40 centimeters or 0.4 meters.
How is the amplitude of the wave defined?
-The amplitude of the wave is defined as the maximum displacement of the particle from the equilibrium position.
What is the amplitude of the wave in the example?
-The amplitude of the wave is 5 centimeters, which can also be written as 0.05 meters.
How can the frequency of the wave be calculated?
-The frequency of the wave can be calculated using the formula: frequency = speed / wavelength. In this example, the speed is 10 meters per second and the wavelength is 0.4 meters, resulting in a frequency of 25 Hz.
What is the frequency of the wave in the example?
-The frequency of the wave is 25 Hz.
How is the period of the wave related to its frequency?
-The period of the wave (T) is the reciprocal of the frequency (F), given by the formula: T = 1 / F.
What is the period of the wave in the example?
-The period of the wave is 0.04 seconds.
Outlines
🌊 Determining Wave Characteristics
In this section, we are introduced to the problem of determining the wavelength, amplitude, frequency, and period of a waveform depicted in figure 8.19. The waveform is shown as a displacement versus distance graph with a given speed of 10 meters per second. The wavelength is calculated by measuring the distance between two consecutive troughs or crests, found to be 40 centimeters or 0.4 meters. The amplitude is identified as the maximum displacement from the equilibrium position, measured as 5 centimeters or 0.05 meters. The frequency is then calculated using the speed and wavelength, resulting in 25 Hz. Finally, the period is determined by taking the inverse of the frequency, yielding 0.04 seconds.
📏 Calculating Frequency and Period
This part continues the calculation of wave characteristics by focusing on the frequency and period. The frequency is derived by dividing the speed of the wave (10 meters per second) by the wavelength (0.4 meters), resulting in 25 Hz. The explanation emphasizes the concept of frequency as the number of oscillations per second, also referred to as Hertz (Hz). Following this, the period of the wave is calculated as the inverse of the frequency, which is 0.04 seconds. The section concludes by reaffirming the simple relationship between frequency and period.
Mindmap
Keywords
💡Wavelength
💡Amplitude
💡Frequency
💡Period
💡Speed
💡Crest
💡Trough
💡Equilibrium Position
💡Oscillation
💡Centimeters to Meters Conversion
Highlights
The speed of the wave is 10 meters per second.
Wavelength can be determined from the distance between two troughs or two crests.
The wavelength is found to be 40 centimeters or 0.4 meters.
Amplitude is the maximum displacement from the equilibrium position.
The amplitude of the wave is 5 centimeters or 0.05 meters.
Frequency can be calculated using the wave's speed and wavelength.
The frequency of the wave is 25 Hz.
Period of the oscillation (T) is the reciprocal of the frequency (F).
The period of the wave is 0.04 seconds.
A complete oscillation can be measured from one trough to the next or one crest to the next.
Snapshot of the waveform helps in visualizing the wave properties.
Displacement vs. distance graph is used to determine the wavelength.
Wavelength determination using the graph: from 10 cm to 50 cm or from 60 cm to 20 cm.
Understanding the relationship between speed, wavelength, and frequency is crucial.
Frequency is expressed in Hertz (Hz), which is cycles per second.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: