18. Wave Theory of Light
TLDRThe transcript is a detailed lecture on the principles of wave optics, focusing on the significance of experiments in physics and how they can lead to the revision of established theories. The professor emphasizes that experiments are crucial for validating or refuting theories, and introduces the concept of interference, a phenomenon that cannot be explained by geometric optics alone. The lecture delves into the famous double-slit experiment, illustrating how light behaves both as a particle and a wave, leading to interference patterns that are dependent on the wavelength of light and the spacing between the slits. The professor also discusses the conditions for constructive and destructive interference, the role of complex numbers in wave analysis, and the application of these principles in understanding phenomena such as diffraction gratings and the colors seen in an oil slick. The lecture concludes with an explanation of why the principle of the equality of incidence and reflection angles (i=r) holds true for light waves during reflection.
Takeaways
- 📚 **Experiments Drive Physics**: The professor emphasizes that experiments are the cornerstone of change in physics. If a theory doesn't align with experimental results, it's considered invalid.
- 🌟 **Theory and Observation**: Newcomers in physics can gain recognition if their predictions, based on new theories, agree with experiments, highlighting the importance of empirical validation.
- 🔍 **Revising Geometric Optics**: The professor mentions that geometric optics needs revision under certain conditions, suggesting that there are limitations to this theory when dealing with very small apertures or high velocities.
- 🚀 **Newtonian Mechanics Limitations**: Newtonian mechanics is described as 'wrong' at high velocities nearing the speed of light, but it's correct within its proper domain, illustrating the concept of a theory's range of applicability.
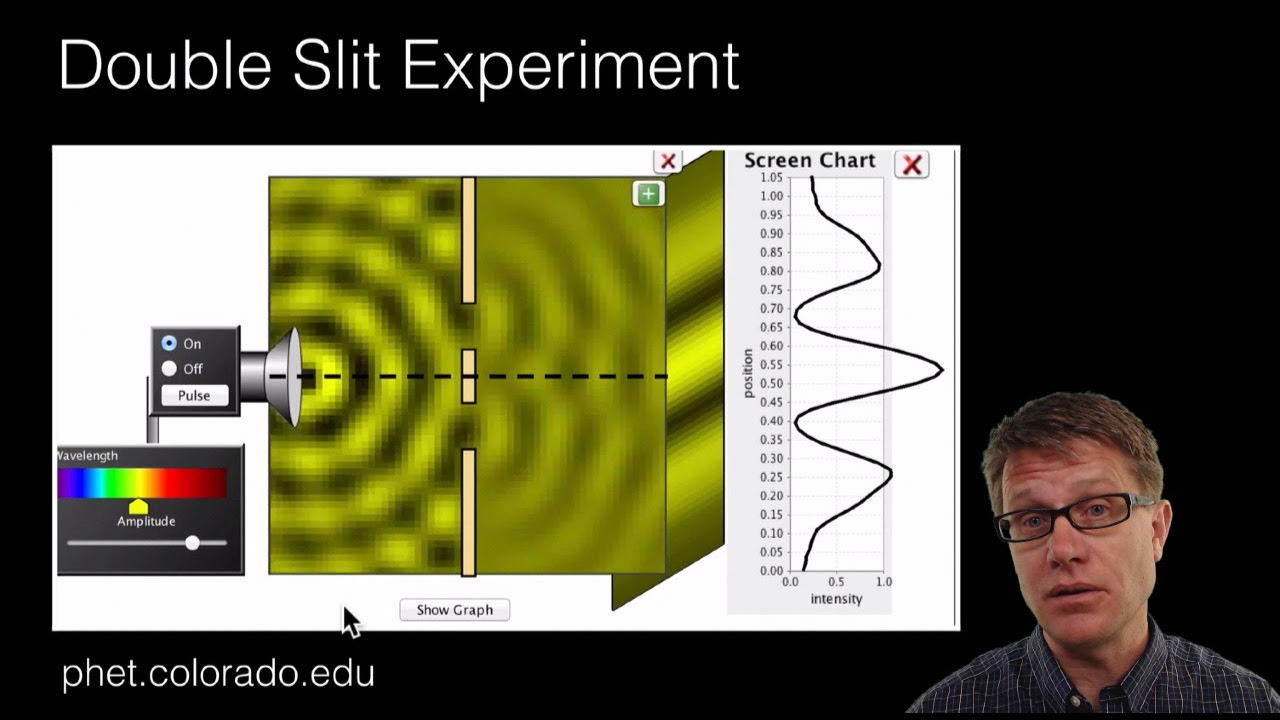
- 🌈 **Interference of Light**: The phenomenon of light interference is explained through the double-slit experiment, where light passing through two slits creates a pattern of bright and dark fringes, indicative of wave behavior.
- 🔬 **Wave Theory and Linearity**: The wave equation, being linear, allows for the principle of superposition, where two wave solutions can be added together to form a new solution, a fundamental concept in wave theory.
- 📊 **Intensity and Square of the Wave Function**: The intensity or energy of a wave is related to the square of the wave function, not the wave function itself, which is crucial for understanding wave-particle duality.
- 🔴 **Complex Numbers in Waves**: The use of complex numbers simplifies the mathematics of wave behavior, especially when dealing with phase shifts and interference patterns.
- 🔎 **Diffraction Grating**: A many-slit setup acts as a diffraction grating, which can separate white light into its component colors due to different wavelengths interfering at different angles.
- 🛠️ **Practical Limitations of Experimentation**: Historically, the belief in geometric optics was due to the inability to create very narrow slits necessary to observe wave optics effects.
- 🌠 **Reflection and Coherence**: For light reflection to occur with the angle of incidence equaling the angle of reflection (i = r), the re-emitted light waves from atoms must be in step, which only happens in specific directions.
Q & A
What is the fundamental reason for revising the principles of geometric optics?
-The fundamental reason for revising geometric optics is that experiments have shown that there are situations where the theory does not hold. In physics, when new experiments contradict a theory, the theory must be revised or replaced.
How does the principle of superposition apply to waves?
-The principle of superposition states that when two or more waves overlap, the resulting wave is the sum of the individual waves. This principle is a consequence of the linearity of the wave equation, meaning that if ψ1 and ψ2 are solutions, so is any linear combination of them.
Why is it necessary to use monochromatic light for observing certain optical phenomena?
-Monochromatic light, which consists of a single wavelength, is necessary to observe certain optical phenomena like interference patterns because multiple wavelengths can interfere with each other and wash out the pattern. Different wavelengths would create different patterns, and their maxima and minima would not coincide, leading to a blurred effect.
What is the relationship between the wavelength of light and the dimensions of an experimental setup for observing wave optics effects?
-To observe wave optics effects, the dimensions of the experimental setup, such as the size of a hole or slit, need to be comparable to the wavelength of the light. When the wavelength is much smaller than the setup, ray optics can be used. However, when the wavelength and the size of the hole are similar, wave optics must be considered.
Why does the intensity of light appear to decrease when a second slit is opened in the double-slit experiment?
-The intensity of light can decrease with a second slit open because of the interference effect. When the light waves from both slits meet, they can interfere constructively or destructively based on their phase difference. If they are out of phase by an odd multiple of half a wavelength, they interfere destructively, leading to a dark spot or decreased intensity on the screen.
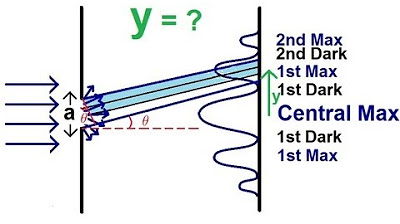
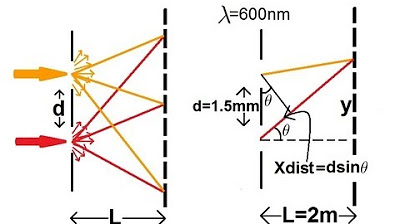
What is the condition for constructive interference in the double-slit experiment?
-Constructive interference occurs when the path difference between the two waves from the slits is an integer multiple of the wavelength (λ). Mathematically, this is represented as δ = mλ, where m is an integer, and δ is the path difference between the two waves.
What is the condition for destructive interference in the double-slit experiment?
-Destructive interference occurs when the path difference between the two waves from the slits is an odd multiple of half the wavelength (λ/2). This can be represented as δ = (2m + 1) * λ/2, where m is an integer.
Why is it that the angle of reflection equals the angle of incidence, as observed in light reflection?
-The angle of reflection equals the angle of incidence because only in this specific angle do all the re-emitted waves from the surface atoms arrive in step, leading to a coherent wave front that results in a strong reflected wave in that direction.
How can the presence of certain elements in a star be determined through spectroscopy?
-The presence of certain elements in a star can be determined through spectroscopy by analyzing the absorption or emission lines in the star's spectrum. Each element has a unique pattern of these lines, which can be used to identify the elements present by matching the observed spectrum with known elemental spectra.
Why do we see a variety of colors in an oil slick on a rainy day?
-The variety of colors seen in an oil slick are due to thin-film interference. When light reflects off the top and bottom surfaces of the oil, different wavelengths (colors) interfere constructively or destructively based on the thickness of the oil slick and the angle of the incoming light, leading to the cancellation or enhancement of certain colors.
What is the role of the linearity of the wave equation in the formation of wave solutions?
-The linearity of the wave equation allows for the principle of superposition to hold, meaning that any linear combination of solutions to the wave equation is also a solution. This property is crucial for the formation of wave solutions, as it enables the combination of different oscillating patterns to form a single, unified wave pattern.
Outlines
🔬 The Role of Experiments in Advancing Physics
The professor emphasizes the critical role of experiments in physics, explaining that they are the only way to revise or confirm theories. He discusses the process of scientific discovery and the importance of experimental evidence in accepting or rejecting a theory. The professor also touches on the historical context of geometric optics and how it was eventually found to be incomplete due to new experimental findings.
🌟 Interference and Diffraction in Wave Optics
The paragraph delves into the concepts of interference and diffraction, which are key phenomena in wave optics. It discusses how light behaves when passing through two holes, creating an interference pattern on a screen. The professor explains the conditions under which constructive and destructive interference occur, leading to bright and dark regions on the screen. The explanation also covers how the size of the holes and the wavelength of light affect the pattern observed.
📐 The Linear Nature of Wave Equations
This section focuses on the mathematical properties of wave equations, highlighting their linearity. The principle of superposition is introduced, which allows for the summation of different wave solutions to the wave equation. The professor also discusses the implications of this linearity for the behavior of wave amplitudes and the calculation of intensity, which is related to the square of the wave's amplitude.
🌈 Intensity and the Significance of Squaring the Wave Function
The professor clarifies that the wave function, denoted as ψ, can be both positive and negative, and thus cannot directly represent physical quantities like brightness, which is always positive. The concept of intensity is introduced as a positive quantity derived from the square of the wave function. The importance of squaring the wave function to obtain a physically meaningful value for intensity is emphasized.
🤔 The Complexities of Quantum Mechanics and Wave Functions
The paragraph introduces the wave function in quantum mechanics, noting its intrinsic complexity and the necessity of considering both the real and imaginary parts of the wave function. The professor explains that in quantum mechanics, the wave function is fundamentally complex, and the intensity or probability density is given by the absolute value squared of the wave function, not just the square.
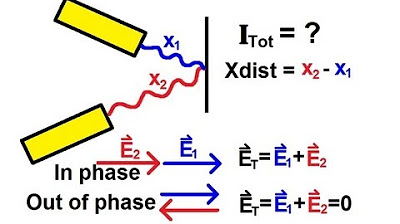
🌀 Vector Addition and the Geometry of Wave Interaction
The professor explores the addition of two wave functions using vector addition, emphasizing the use of complex numbers to simplify calculations. The vector sum of two waves is shown to result in a new wave with an amplitude that can vary depending on the phase difference between the original waves. The concept of phase shift and its effect on the resulting wave's amplitude is discussed in detail.
🚫 The Limitations of Geometrical Optics and the Rise of Wave Optics
This section discusses the historical shift from geometrical optics to wave optics. The professor explains that as the technology advanced to produce very narrow slits and monochromatic light, the wave nature of light became evident. The limitations of geometrical optics are highlighted, particularly when the size of the aperture is comparable to the wavelength of light.
🎛️ Diffraction Gratings and the Dispersion of Light
The professor describes how a diffraction grating, a tool with evenly spaced lines, can act as a prism and disperse white light into its constituent colors. This dispersion is due to the different wavelengths of light being diffracted by different amounts, leading to a separation of colors in the observed pattern. The conditions for constructive interference for different colors are also discussed.
🛑 The Phenomenon of Diffraction and Its Impact on Image Formation
The final paragraph addresses the phenomenon of diffraction, explaining why light spreads out when passing through an aperture. The professor illustrates how the size of the aperture in relation to the wavelength of light determines the degree of spreading. The concept of diffraction minima is introduced, explaining the conditions that lead to the formation of dark fringes in the light pattern.
Mindmap
Keywords
💡Geometric Optics
💡Experimentation
💡Theory
💡Interference
💡Wave Equation
💡Superposition Principle
💡Intensity
💡Complex Numbers
💡Phase
💡Diffraction
💡Wavelength
Highlights
The importance of experiments in physics for validating and updating theories.
The concept that theories in physics are only as good as their agreement with experimental results.
The idea that new experiments can reveal shortcomings in existing theories, necessitating revisions.
The historical context of Newtonian mechanics being superseded by Einstein's theory of relativity under certain conditions.
The principle that new theories should encompass and explain the successes of old theories within their domain of validity.
The phenomenon of light spreading out beyond the geometric image of an aperture as the aperture size decreases.
The role of interference experiments in disproving classical ray theories and demonstrating the wave nature of light.
The conditions required to observe interference patterns, such as using monochromatic light and apparatus dimensions comparable to the wavelength.
The wave equation and its implications for the behavior of waves, including the principle of superposition.
The concept that the intensity of light, as a measure of energy or brightness, is proportional to the square of the wave function.
The use of complex numbers and the absolute value squared to represent the wave function in quantum mechanics.
The interference pattern produced by the double-slit experiment and its explanation of the wave nature of light.
The diffraction grating and its use in splitting light into its component colors, acting as a prism.
The reason why the law of reflection (i = r) holds true for waves, based on the phase of emitted light from atoms.
The phenomenon of thin-film interference, such as the colorful patterns seen in oil slicks, due to light waves interfering after reflecting off different layers.
The significance of understanding geometric optics' limitations and the transition to wave optics when dealing with small apertures or high-purity light.
The historical progression of understanding in physics, from trusting in geometric optics to the discovery of wave optics through technological advancements.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: