Integral of tan^4 (theta) | MIT 18.01SC Single Variable Calculus, Fall 2010
TLDRIn this educational video, Christine Breiner guides viewers through the process of finding the anti-derivative of the function 'tangent theta to the fourth power'. She utilizes a trigonometric identity, \(1 + \tan^2(\theta) = \sec^2(\theta)\), to simplify the integral and employs substitution strategies for even powers of tangent. The method involves breaking down the integral into manageable parts, applying the identity, and using substitution to simplify the integration process. The video concludes with a clear demonstration of how to tackle even powers of tangent functions for anti-derivatives, highlighting a reduction formula approach.
Takeaways
- 📚 The video focuses on finding the anti-derivative of a trigonometric function, specifically the power of the tangent function.
- 🔍 The instructor introduces the problem by asking students to find the anti-derivative of \(\tan^4(\theta)\).
- 📝 A key trigonometric identity is highlighted: \(1 + \tan^2(\theta) = \sec^2(\theta)\), which is crucial for solving the integral.
- 🔑 The strategy involves breaking down \(\tan^4(\theta)\) into the product of two \(\tan^2(\theta)\) terms and then using the identity to rewrite the integral.
- 🧩 The integral is rewritten as \(\int \sec^2(\theta) - 1 \, d\theta\), which simplifies the problem into more manageable parts.
- 📉 The integral is further decomposed into two separate integrals: \(\int \tan^2(\theta) \sec^2(\theta) \, d\theta\) and \(\int \tan^2(\theta) \, d\theta\).
- 🔄 The even powers of the tangent function are particularly advantageous for integration due to the properties of the derivative of the tangent function.
- ✂️ The substitution method is used for the first integral, where \(u = \tan(\theta)\) and \(ds = \sec^2(\theta) \, d\theta\).
- 🔍 For the second integral, the trigonometric identity is used again to express \(\tan^2(\theta)\) as \(\sec^2(\theta) - 1\), allowing for easier integration.
- 📈 The final solution involves integrating \(\sec^2(\theta)\) and \(1\), which are straightforward due to their derivatives being known.
- 🔚 The instructor concludes by emphasizing the usefulness of the strategy for even powers of tangent and hints at a reduction formula that could be derived from this process.
Q & A
What is the main topic of the recitation video?
-The main topic of the recitation video is to find the anti-derivative of a trigonometric function, specifically the anti-derivative of tangent theta to the fourth power.
What trigonometric identity is suggested to be used in the video?
-The trigonometric identity suggested to be used in the video is \(1 + \tan^2(\theta) = \sec^2(\theta)\).
How does the video suggest breaking down the integral of tangent theta to the fourth power?
-The video suggests breaking down the integral by rewriting it as the product of two tangent squared thetas and then using the identity \(1 + \tan^2(\theta) = \sec^2(\theta)\) to transform it into an integral of secant squared theta minus 1.
What is the significance of using even powers of tangent theta in the integral?
-Using even powers of tangent theta makes the integral easier to handle because it allows for the use of the trigonometric identity and simplifies the process of integration using substitution.
What substitution is used in the video to simplify the integral of secant squared theta times tangent squared theta?
-The substitution used in the video is \(u = \tan(\theta)\), which leads to \(du = \sec^2(\theta) d\theta\), simplifying the integral to \(\int u^2 du\).
What is the result of the substitution for the integral of secant squared theta times tangent squared theta?
-The result of the substitution is \(\int u^2 du\), which integrates to \(\frac{u^3}{3}\), or in terms of the original variable, \(\frac{\tan^3(\theta)}{3}\).
How does the video approach the integral of tangent squared theta d theta without secant squared theta?
-The video approaches this by using the trigonometric identity again, replacing \(\tan^2(\theta)\) with \(\sec^2(\theta) - 1\), allowing for easier integration of the secant squared theta and the constant 1.
What are the final steps in integrating the modified integral of tangent squared theta d theta?
-The final steps involve integrating secant squared theta to get tangent theta, integrating the constant 1 to get theta, and then combining these results with the substitution result and adding the constant of integration.
What is the significance of the strategy used in the video for finding anti-derivatives of powers of tangent functions?
-The strategy used in the video is significant because it demonstrates a method to reduce the complexity of integrating powers of tangent functions by using trigonometric identities and substitution, which can lead to a reduction formula.
Why is the process easier when dealing with even powers of tangent theta?
-The process is easier with even powers of tangent theta because it allows for the use of the identity \(1 + \tan^2(\theta) = \sec^2(\theta)\) to simplify the integral into a form that can be repeatedly integrated using substitution, leading to a more straightforward solution.
How does the video relate the process of finding anti-derivatives of powers of tangent to reduction formulas?
-The video relates the process to reduction formulas by showing that by repeatedly applying the strategy of using the trigonometric identity and substitution, one can reduce the power of the tangent function in the integral, similar to how reduction formulas simplify complex integrals.
Outlines
📚 Introduction to Finding Anti-derivatives of Trigonometric Functions
Christine Breiner introduces the topic of finding anti-derivatives, specifically focusing on the anti-derivative of the tangent function raised to the fourth power. She emphasizes the importance of using familiar trigonometric identities and other strategies to solve the problem. The hint provided is the identity \(1 + \tan^2(\theta) = \sec^2(\theta)\), which will be instrumental in simplifying the integral.
🔍 Utilizing Trigonometric Identities to Simplify the Integral
The video script details a step-by-step process to find the anti-derivative of \(\tan^4(\theta)\). The strategy involves rewriting the expression using the identity \(\sec^2(\theta) - 1 = \tan^2(\theta)\), which allows the integral to be split into two parts: one involving \(\sec^2(\theta)\) and the other \(\tan^2(\theta)\). The first part is simplified using substitution with \(u = \tan(\theta)\), leading to an integral of \(u^2\), which is straightforward to solve. The second part is further simplified by recognizing that \(\sec^2(\theta)\) is the derivative of \(\tan(\theta)\), making the integration of \(\sec^2(\theta)\) straightforward. The final solution is obtained by integrating these simplified expressions and adding a constant of integration.
Mindmap
Keywords
💡Anti-derivatives
💡Trigonometric function
💡Tangent
💡Trigonometric identities
💡Secant
💡U-substitution
💡Integration
💡Reduction formulas
💡Even powers
💡Derivative
💡Constant of integration
Highlights
Introduction to the task of finding anti-derivatives of trigonometric functions, specifically the power of the tangent function.
The challenge of finding an anti-derivative of tangent theta to the fourth power is presented.
Emphasis on the use of familiar trigonometric identities to simplify the problem.
Introduction of the trigonometric identity 1 + tan^2(theta) = sec^2(theta) as a key to solving the integral.
Strategy to break down the integral of tan^4(theta) into the product of two tan^2(theta) terms.
Transformation of the integral using the secant squared identity to simplify the expression.
The use of u-substitution for even powers of tangent functions to facilitate integration.
Explanation of why even powers of tangent are easier to integrate due to the derivative of tangent being secant squared.
Application of the identity to rewrite tan^2(theta) as sec^2(theta) - 1 for further simplification.
Integration of secant squared theta by recognizing it as the derivative of tangent function.
The process of integrating 1 d theta to obtain a linear term in theta.
Final integration steps leading to the solution with tan^3(theta)/3, tan(theta), and theta terms.
Inclusion of a constant 'c' to represent the family of possible anti-derivatives.
Discussion on the applicability of the method to any power of tangent, not just even powers.
Mention of the reduction formulas and how they relate to the process used in the video.
Highlighting the preference for even powers due to the ease of applying the method repeatedly.
Conclusion summarizing the strategy used to find anti-derivatives of powers of tangent functions.
Transcripts
Browse More Related Video

Integrals: Trig Substitution 2

Integrating sin^n(x) Using Reduction | MIT 18.01SC Single Variable Calculus, Fall 2010
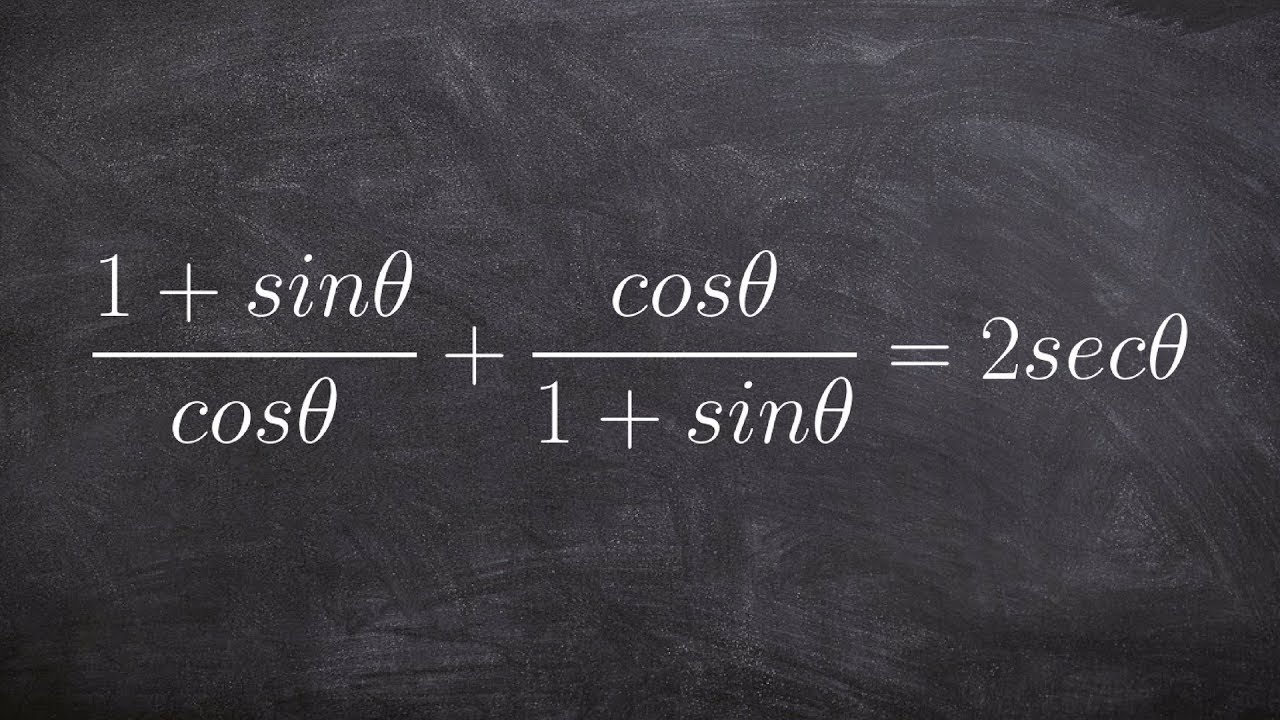
Verifying a trigonometric Identities

Finding u and v' When Integrating by Parts | MIT 18.01SC Single Variable Calculus, Fall 2010

Trig Integrals and a Volume of Revolution | MIT 18.01SC Single Variable Calculus, Fall 2010

Integrals: Trig Substitution 1
5.0 / 5 (0 votes)
Thanks for rating: