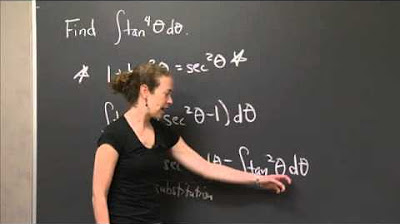Finding u and v' When Integrating by Parts | MIT 18.01SC Single Variable Calculus, Fall 2010

MIT OpenCourseWare

7 Jan 201111:38

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Christine Breiner guides viewers through the process of integration by parts, focusing on finding antiderivatives for four complex functions. She emphasizes the importance of correctly choosing 'u' and 'v prime' to simplify the integration process. Breiner provides strategies and hints for each problem, including a nontraditional approach for the second function, and reminds viewers of the integration by parts formula. She concludes with the final answers for each problem, reinforcing the understanding of when to apply integration by parts effectively.

Takeaways

📚 The video focuses on practicing integration by parts to find antiderivatives for four specific functions.
🔍 The importance of choosing the correct 'u' and 'v prime' in integration by parts is emphasized for simplifying the process.
💡 A hint is provided for the second problem, suggesting a nontraditional way to split the function in the numerator.
📝 The integration by parts formula is integral of u*v prime dx = u*v - integral of v*u prime dx + constant (c).
🎯 For the first problem, 'x' is chosen as 'u' and 'e to the minus x' as 'v prime' to simplify the integration.
🧩 The second problem involves rewriting the function to make it easier to integrate by parts, focusing on the derivative of '1 plus x squared'.
📉 In the third problem, 'arctan x' is treated as 'u' and '1' as 'v prime', leveraging the derivative of 'arctan x' for easier integration.
📚 For the fourth problem, 'ln x' is chosen as 'u' with its derivative simplifying the integration process, avoiding the complexity of integrating 'ln x' directly.
🔑 The strategy for choosing 'u' and 'v prime' is to make the integration of 'v u prime' as simple as possible.
📈 The video provides final answers for each problem, allowing viewers to compare their work and understanding.
🤓 The main goal is to develop an understanding of the strategies involved in choosing 'u' and 'v prime' during integration by parts.

Q & A

What is the main topic of the video?
-The main topic of the video is practicing integration by parts to find antiderivatives for four given functions.
What are the four functions for which the antiderivatives are being found?
-The four functions are x * e^(-x), x^3 / (1 + x^2)^2, arctan(x), and ln(x) / x^2.
What is the purpose of choosing 'u' and 'v prime' in integration by parts?
-The purpose of choosing 'u' and 'v prime' in integration by parts is to simplify the integration process by making the resulting integral as simple as possible.
Why is the function x^3 / (1 + x^2)^2 split in a nontraditional way?
-The function is split in a nontraditional way to make the integration process simpler by dealing with the denominator and making the function easier to integrate.
What is the integration by parts formula?
-The integration by parts formula is ∫u dv = uv - ∫v du + C.
For the function x * e^(-x), what is chosen as 'u' and why?
-For the function x * e^(-x), 'u' is chosen to be x because its derivative is 1, which simplifies the integration process.
What substitution strategy is used for the function x^3 / (1 + x^2)^2?
-A substitution strategy is used to integrate the function by making the denominator part of 'v prime' and integrating it, which simplifies the process.
What is the derivative of arctan(x) and how does it help in integration by parts?
-The derivative of arctan(x) is 1 / (1 + x^2). It helps in integration by parts by simplifying the integration process when arctan(x) is chosen as 'u'.
Why is ln(x) not chosen as 'v prime' in integration by parts?
-Ln(x) is not chosen as 'v prime' because its antiderivative is more complex, and its derivative (1/x) simplifies the integration process when ln(x) is chosen as 'u'.
What are the final answers for the antiderivatives of the four functions?
-The final answers are: for x * e^(-x), it's -x * e^(-x) - e^(-x) + C; for x^3 / (1 + x^2)^2, it's -x^2 / (2 * (1 + x^2)) + 1/2 * ln(1 + x^2) + C; for arctan(x), it's x * arctan(x) - 1/2 * ln(1 + x^2) + C; and for ln(x) / x^2, it's -ln(x) / x - 1/x + C.

Outlines

00:00

📚 Introduction to Integration by Parts

Christine Breiner introduces the topic of the video, which is practicing integration by parts. She presents four problems to the audience, encouraging them to find the antiderivatives of given functions. She emphasizes the importance of choosing the correct 'u' and 'v prime' for the integration by parts formula and hints at a nontraditional approach for the second problem. The formula for integration by parts is also reiterated for clarity.

05:01

🔍 Strategies for Choosing 'u' and 'v prime'

The speaker discusses the strategy for choosing 'u' and 'v prime' in integration by parts, using the first problem as an example. She explains the process of selecting 'u' and 'v prime' based on simplicity and the ease of integration. She also provides a hint for the second problem, suggesting a nontraditional way to split the function in the numerator. The explanation includes a detailed look at the integration by parts formula and how to apply it to the given functions.

10:10

📘 Detailed Walkthrough of Integration by Parts Problems

Christine provides a detailed walkthrough of the integration by parts process for the first two problems. She explains how to integrate the functions by choosing appropriate 'u' and 'v prime' values and using substitution where necessary. The explanation includes the reasoning behind the choices and the steps to follow for integration. She also discusses the derivative of arctan(x) and how it relates to the integration process, setting up the groundwork for the third problem.

📝 Conclusion and Final Answers

In the final part of the script, Christine summarizes the process and provides the final answers to the integration by parts problems. She emphasizes the importance of understanding which function to choose as 'u' and which as 'v prime' to simplify the integration process. The solutions for all four problems are presented, and she encourages the audience to compare their answers with the provided solutions to ensure understanding.

Mindmap

Keywords

💡Integration by Parts

Integration by Parts is a specialized method in calculus for finding the integral (antiderivative) of a product of two functions. In the video, the theme revolves around practicing this technique to solve complex integrals. The script provides examples of how to apply this method to different functions, emphasizing the selection of 'u' and 'v prime' to simplify the integration process.

💡Antiderivative

An antiderivative is a function that represents the reverse process of differentiation. The video focuses on finding antiderivatives of given functions using integration by parts. The script mentions the goal of determining 'u' and 'v prime' to facilitate finding the antiderivative, as seen in the practice problems provided.

💡u and v prime

In the context of integration by parts, 'u' and 'v prime' are the components of the product being integrated. The script explains the strategy of choosing 'u' and 'v prime' to simplify the integration process, with examples showing how different choices can affect the complexity of the resulting integral.

💡Substitution

Substitution is a technique used in calculus to simplify the integration of complex functions by replacing them with simpler expressions. The script mentions using substitution to integrate a part of the function in the second problem, where 'x^3/(1 + x^2)^2' is rewritten to facilitate easier integration.

💡Derivative

A derivative in calculus measures how a function changes as its input changes. The script discusses the derivatives of functions like 'arctan(x)' and 'ln(x)', which are crucial for determining 'u' and 'v prime' in the integration by parts formula.

💡Natural Logarithm (ln x)

The natural logarithm is the logarithm to the base 'e' and is used in calculus for solving exponential and logarithmic functions. In the script, 'ln x' is one of the functions for which the antiderivative is found using integration by parts, with a focus on its derivative being '1/x'.

💡Arctangent (arctan x)

Arctangent is the inverse trigonometric function of tangent and is used in calculus for integrating functions involving '1/(1 + x^2)'. The script illustrates how 'arctan x' is integrated by parts, highlighting its derivative '1/(1 + x^2)'.

💡Exponential Function

An exponential function is a function of the form 'a^x', where 'a' is a constant. The script includes 'x * e^(-x)' as an example where the exponential function is integrated by parts, showing how the derivative and integral of 'e^(-x)' simplify the process.

💡Power Rule

The power rule is a basic principle in calculus for integrating functions of the form 'x^n', where 'n' is a constant. The script refers to the power rule when integrating 'v * u prime' in the context of integration by parts, particularly for the function 'ln x / x^2'.

💡Trigonometric Functions

Trigonometric functions, such as sine and cosine, are fundamental in calculus for dealing with periodic functions. Although not explicitly integrated by parts in the script, the mention of 'arctan x' relates to the broader family of trigonometric functions and their integration techniques.

💡Complex Integration

Complex integration refers to the process of integrating functions that are not easily solvable by basic integration techniques. The script discusses strategies for tackling complex integrals, such as breaking them up or using nontraditional methods, as illustrated in the second problem.

Highlights

Introduction to the concept of integration by parts and its application to solve four specific problems.

The importance of identifying the correct functions for u and v' in integration by parts.

A hint provided for the second problem suggesting a nontraditional way to split the function in the numerator.

Explanation of the integration by parts formula and its application in finding antiderivatives.

Choosing u as x and v' as e to the minus x for the first problem to simplify the integration process.

The strategy of rewriting the second function to make the integration by parts process more straightforward.

Use of substitution to integrate the second function after choosing appropriate u and v'.

The reasoning behind choosing u and v' for the second problem to simplify the integration of the denominator.

The trick of considering arctan x as a product with 1 to facilitate the integration by parts process.

Derivative of arctan x and its role in simplifying the integration by parts for the third problem.

The approach to integrate arctan x by making it u and 1 as v', leading to a simpler integration process.

Avoiding making natural log x as v' due to its complex antiderivative, instead choosing it as u for easier integration.

Derivative of natural log x and its use in simplifying the integration by parts for the fourth problem.

The final answers for all four problems are provided, showcasing the outcomes of the integration by parts method.

Emphasis on understanding the selection of u and v' in integration by parts as the main goal of the exercise.

The exercise aims to develop a deep understanding of the strategies involved in integration by parts.

Transcripts

Browse More Related Video

Integration by Parts

Integral of tan^4 (theta) | MIT 18.01SC Single Variable Calculus, Fall 2010

Integration by parts

Integral of a Product

Integration by Parts... How? (NancyPi)

Math1325 Lecture 13 6