Bayes theorem, the geometry of changing beliefs
TLDRThis video delves into Bayes' theorem, a fundamental formula in probability crucial for scientific discovery, machine learning, and AI. It uses the example of Steve to illustrate how new evidence updates prior beliefs, emphasizing the importance of considering relevant facts and ratios in decision-making.
Takeaways
- 📚 Bayes' theorem is a fundamental formula in probability, crucial for scientific discovery, machine learning, AI, and even treasure hunting.
- 🧠 Understanding Bayes' theorem involves knowing the parts, why it's true, and recognizing when to use it.
- 👨🏫 The example of Steve illustrates the irrationality in human judgment when not considering relevant statistical information.
- 📊 Kahneman and Tversky's work highlights how human judgments often contradict probability laws, emphasizing the importance of considering relevant facts.
- 🌐 The ratio of farmers to librarians in the US is used as an example to demonstrate the need to incorporate statistical information in judgments.
- 🔍 Rationality is about recognizing relevant facts, not just knowing them.
- 📈 Bayes' theorem helps update beliefs based on new evidence, emphasizing that evidence should not completely determine beliefs but update prior beliefs.
- 📐 The formula of Bayes' theorem can be visualized and understood through a representative sample or geometrically as areas in a square.
- 🤔 Thinking with a representative sample or geometrically helps make probability more intuitive and captures the continuous nature of probability.
- 💡 Bayes' theorem is not just about uncertainty but about quantifying belief, which is significant in science, AI, and personal thought processes.
Q & A
What is Bayes' theorem and why is it important?
-Bayes' theorem is a fundamental formula in probability that describes how to update the probabilities of hypotheses when given new evidence. It is crucial in scientific discovery, machine learning, AI, and even treasure hunting, as it helps in making informed decisions based on changing evidence and beliefs.
How did Tommy Thompson use Bayesian search tactics in the 1980s?
-Tommy Thompson led a team that used Bayesian search tactics to uncover a ship that had sunk a century and a half earlier. The ship was carrying gold worth about $700 million in today's terms, demonstrating the practical application of Bayes' theorem in real-world scenarios.
What is the significance of understanding the different levels of understanding Bayes' theorem?
-Understanding Bayes' theorem at different levels allows one to not only plug in numbers (basic understanding) but also to grasp why the theorem is true (deeper understanding) and to recognize when to apply it (most important level). This comprehensive understanding is essential for effective application in various fields.
What is the example of Steve used to illustrate irrationality in human judgments?
-The example of Steve, described as shy, withdrawn, and detail-oriented, is used to show how people's judgments often irrationally contradict probability laws. Most people judge Steve to be more likely a librarian than a farmer based on stereotypes, ignoring the fact that there are significantly more farmers than librarians.
What is the role of the ratio of farmers to librarians in the Steve example?
-The ratio of farmers to librarians is crucial in the Steve example because it highlights the importance of considering base rates in probability judgments. Kahneman and Tversky argue that people often fail to incorporate this ratio into their judgments, leading to irrational conclusions.
How does the concept of 'prior' relate to Bayes' theorem?
-In Bayes' theorem, the 'prior' refers to the probability that a hypothesis is true before considering new evidence. It is the starting point for updating beliefs based on new information, and it plays a critical role in determining the final probability (posterior) after the evidence is taken into account.
What is the 'likelihood' in the context of Bayes' theorem?
-The 'likelihood' in Bayes' theorem is the probability of observing the evidence given that the hypothesis is true. It is used to compare how well different hypotheses can explain the observed evidence.
How does Bayes' theorem help in updating beliefs based on evidence?
-Bayes' theorem provides a mathematical framework for updating beliefs by incorporating new evidence. It shows that new evidence should not completely determine beliefs but should update them based on the prior probability and the likelihood of the evidence given the hypothesis.
What is the significance of the 'posterior' in Bayes' theorem?
-The 'posterior' in Bayes' theorem is the updated probability of a hypothesis being true after considering new evidence. It represents the revised belief about the hypothesis, taking into account both the prior probability and the likelihood of the evidence.
How does the diagram of a representative sample help in understanding Bayes' theorem?
-The diagram of a representative sample helps visualize the process of updating beliefs by showing how the space of possibilities is restricted by new evidence. It allows for a more intuitive understanding of how probabilities change and how the theorem can be applied in various scenarios.
What are some broader takeaways about making probability more intuitive?
-Broader takeaways include the importance of thinking about representative samples and using geometric representations to make probability more intuitive. These methods help in understanding continuous nature of probability and the math of proportions, which underlies all probability formulas.
What is the debate about the rationality of considering the ratio of farmers to librarians in the Steve example?
-The debate centers on whether it is rational to consider the ratio of farmers to librarians when judging the likelihood of Steve being a librarian. Some psychologists argue that the context is ambiguous and that the prior should be based on more specific information about Steve, highlighting the importance of context in probability judgments.
Outlines
📚 Understanding Bayes' Theorem
This paragraph introduces Bayes' theorem as a fundamental concept in probability, crucial for scientific discovery, machine learning, AI, and even treasure hunting. It emphasizes the importance of understanding not just the formula itself, but also its application in updating beliefs based on new evidence. The example of Steve, a librarian or a farmer, is used to illustrate how people often make irrational judgments without considering relevant statistical information. The paragraph also highlights the need to recognize when to apply Bayes' theorem and the importance of considering the ratio of different groups in making judgments.
🧩 Breaking Down Bayes' Theorem
This paragraph delves deeper into Bayes' theorem, explaining the concept of 'prior' probability, which is the initial belief before new evidence is considered. It introduces the 'likelihood' as the probability of observing the evidence given the hypothesis is true. The paragraph also discusses the need to consider the probability of seeing the evidence if the hypothesis is false. Using the example of Steve, the paragraph shows how to calculate the 'posterior' probability, which is the updated belief after considering the evidence. The importance of understanding the formula and its application in various fields, such as science and AI, is reiterated.
📉 Probability and Intuition
This paragraph explores broader concepts in probability beyond Bayes' theorem, focusing on how to make probability more intuitive. It discusses the Kahneman and Tversky experiment with Linda, highlighting a common error in probability judgments and how thinking in terms of representative samples can help. The paragraph also emphasizes the continuous nature of probability and the usefulness of geometric representations, such as areas, in understanding probability. The discussion touches on the debate around the rationality of incorporating ratios in judgments and the importance of updating beliefs with evidence, rather than letting evidence solely determine beliefs.
Mindmap
Keywords
💡Bayes' Theorem
💡Scientific Discovery
💡Machine Learning
💡AI (Artificial Intelligence)
💡Treasure Hunting
💡Steve
💡Daniel Kahneman and Amos Tversky
💡Rationality
💡Prior
💡Likelihood
💡Posterior
Highlights
Bayes' theorem is a crucial formula in probability, central to scientific discovery, machine learning, and AI.
Bayes' theorem was used in treasure hunting in the 1980s to uncover a shipwreck carrying $700 million worth of gold.
Understanding Bayes' theorem involves knowing its parts, why it's true, and recognizing when to use it.
The example of Steve being a librarian or a farmer illustrates the use of Bayes' theorem in human judgment.
Kahneman and Tversky's study on human judgments won a Nobel Prize and popularized the concept of irrationality in probability.
People often fail to incorporate the ratio of farmers to librarians in their judgments, which Kahneman and Tversky argue is irrational.
Rationality in judgment is about recognizing relevant facts, not just knowing them.
Bayes' theorem involves updating beliefs based on new evidence, not just accepting new evidence as truth.
The probability that a random person fitting a description is a librarian is calculated using Bayes' theorem.
The key to Bayes' theorem is that new evidence should update prior beliefs, not replace them.
Bayes' theorem can be generalized to any hypothesis and evidence, helping determine the probability of a hypothesis given evidence.
The prior probability, likelihood, and total probability of evidence are essential components of Bayes' theorem.
The posterior probability represents the updated belief about a hypothesis after considering new evidence.
Bayes' theorem is used in science to validate or invalidate models and in AI to model a machine's belief.
Bayes' theorem can be visualized using a representative sample or geometrically, aiding in intuitive understanding.
Thinking in terms of proportions and areas can make probability more intuitive and applicable.
Kahneman and Tversky's experiment with Linda showed how framing questions can affect intuitive probability judgments.
Bayes' theorem is about updating beliefs based on evidence, a concept that can be debated in psychology but is mathematically sound.
Transcripts
Browse More Related Video
You Know I'm All About that Bayes: Crash Course Statistics #24
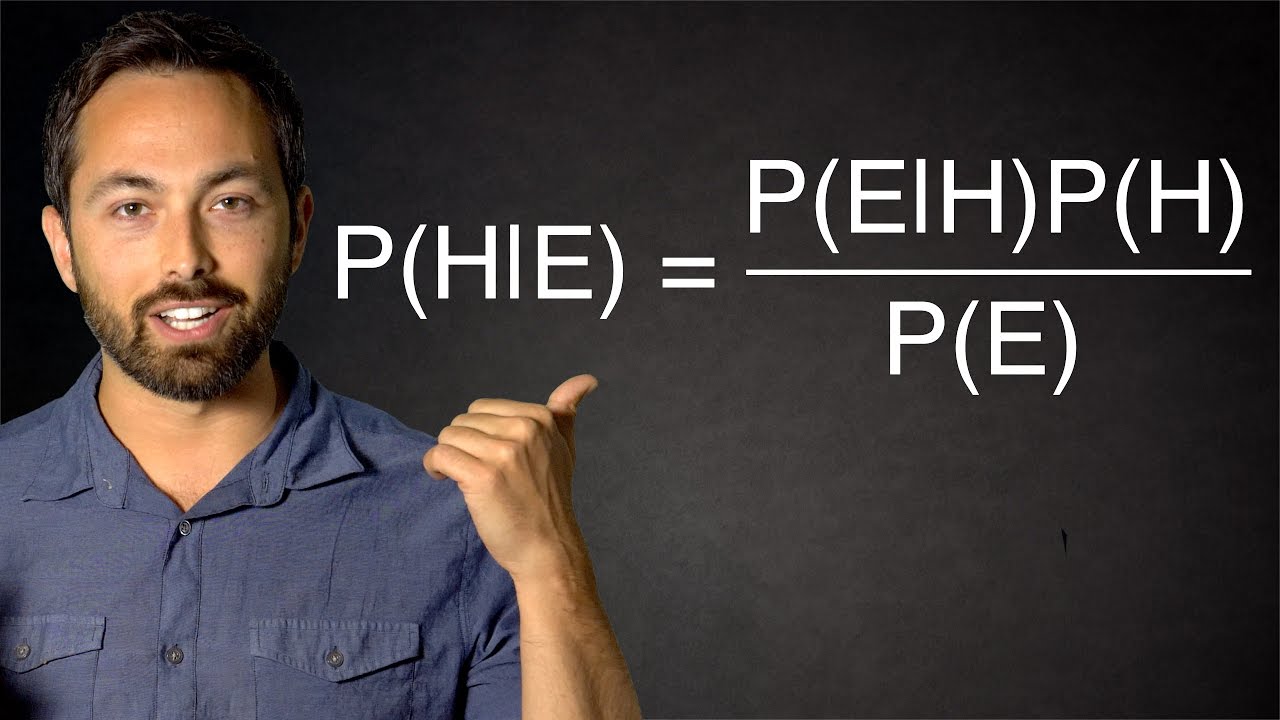
The Bayesian Trap

Probability Part 2: Updating Your Beliefs with Bayes: Crash Course Statistics #14

Bayes in Science and Everyday Life: Crash Course Statistics #25
6.4.3 The Central Limit Theorem - The Rare Event Rule and the Central Limit Theorem

Likelihood Ratios Explained
5.0 / 5 (0 votes)
Thanks for rating: