5.6.1 Law of Cosines: Solving Triangles (SAS, SSS)

Justin Backeberg
18 Mar 202007:13
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial demonstrates how to solve triangles using the Law of Cosines, focusing on SAS and SSS scenarios. It covers the three forms of the Law of Cosines and provides step-by-step calculations to find missing sides and angles, using examples with given side lengths and angles.

Takeaways
  • 📚 The video discusses solving triangles using the Law of Cosines in two scenarios: SAS (Side-Angle-Side) and SSS (Side-Side-Side).
  • 📐 The Law of Cosines has three forms, each corresponding to the different sides and angles of a triangle.
  • 🔍 In the first example, the video demonstrates solving for side C given side a (11), side b (5), and angle C (20 degrees).
  • 🧮 The formula used to find side C is C² = a² + b² - 2ab * cos(C), which is then solved to find C ≈ 6.53.
  • 🔑 To find the missing angles, the video uses the Law of Cosines to isolate and calculate the cosine of angle a, leading to angle a ≈ 144.80 degrees.
  • 📈 The remaining angle, angle B, is found by subtracting the known angles from 180 degrees, resulting in angle B ≈ 15.20 degrees.
  • 🔄 The second example involves solving a triangle with all three sides known (a = 9, b = 7, c = 5) and starts with finding angle a.
  • 📘 The formula for angle a when all sides are known is a² = b² + c² - 2bc * cos(a), which is rearranged to isolate cos(a).
  • 📊 By applying the inverse cosine function, angle a is calculated to be approximately 95.74 degrees.
  • ➗ To find angle B, a similar process is followed using the Law of Cosines formula rearranged for angle B, resulting in angle B ≈ 50.70 degrees.
  • 🔚 Finally, angle C is determined by subtracting the sum of angles a and B from 180 degrees, giving angle C ≈ 33.56 degrees.
  • 👍 The video concludes with the complete set of missing information for both examples, demonstrating the application of the Law of Cosines.
Q & A

  • What are the three forms of the law of cosines mentioned in the script?

    -The three forms of the law of cosines are: a² = b² + c² - 2bc * cos(A), b² = a² + c² - 2ac * cos(B), and c² = a² + b² - 2ab * cos(C).

  • In the first example, what information is given to solve the triangle?

    -In the first example, side a is 11, side b is 5, and angle C is 20 degrees.

  • How is side C calculated using the law of cosines in the first example?

    -Side C is calculated using the formula c² = a² + b² - 2ab * cos(C). Plugging in the given values, c² = 11² + 5² - 2 * 11 * 5 * cos(20°). This gives c² ≈ 42.63, and taking the square root, c ≈ 6.53.

  • How is angle A found after calculating side C in the first example?

    -Angle A is found using the rearranged law of cosines formula for angle A: cos(A) = (a² - b² - c²) / (-2bc). Substituting the known values and taking the inverse cosine, angle A ≈ 144.80 degrees.

  • What is the final step to find angle B in the first example?

    -To find angle B, subtract the known angles from 180 degrees: angle B = 180° - 20° - 144.80° ≈ 15.20 degrees.

  • What are the final results for the missing side and angles in the first example?

    -The missing side C is approximately 6.53, angle A is approximately 144.80 degrees, and angle B is approximately 15.20 degrees.

  • What information is given to solve the triangle in the second example?

    -In the second example, all three sides are given: side a is 9, side b is 7, and side c is 5.

  • How is angle A calculated in the second example?

    -Angle A is calculated using the formula a² = b² + c² - 2bc * cos(A), rearranged to solve for cos(A). Plugging in the values and taking the inverse cosine, angle A ≈ 95.74 degrees.

  • How is angle B found in the second example?

    -Angle B is found using the formula b² = a² + c² - 2ac * cos(B), rearranged to solve for cos(B). Substituting the known values and taking the inverse cosine, angle B ≈ 50.70 degrees.

  • What is the final step to find angle C in the second example?

    -To find angle C, subtract the known angles from 180 degrees: angle C = 180° - 95.74° - 50.70° ≈ 33.56 degrees.

  • What are the final results for the missing angles in the second example?

    -The missing angles are approximately 95.74 degrees for angle A, 50.70 degrees for angle B, and 33.56 degrees for angle C.

Outlines
00:00
📚 Introduction to Law of Cosines for Triangles

This paragraph introduces the concept of solving triangles using the Law of Cosines, specifically for scenarios where two sides and the included angle (SAS) or all three sides (SSS) are known. The Law of Cosines is presented in three forms, each corresponding to a different set of known variables. The first example involves finding the missing side C of a triangle with sides a=11, b=5, and angle C=20 degrees. The process involves plugging the known values into the appropriate Law of Cosines formula, calculating C squared, and then taking the square root to find the length of side C. Following this, the paragraph discusses finding the remaining angles of the triangle using the Law of Cosines and basic trigonometric identities.

05:01
🔍 Solving Triangles with All Sides Known

The second paragraph delves into solving a triangle when all three sides are given: a=9, b=7, and c=5. The focus is on finding the angles of the triangle using the Law of Cosines. The process begins by isolating the cosine of angle a using the formula and then calculating it using the known side lengths. An inverse cosine function is applied to find the measure of angle a. The method is then repeated for angle B, again using the Law of Cosines with the appropriate formula. Finally, by using the fact that the sum of angles in a triangle equals 180 degrees, angle C is determined by subtraction. The paragraph concludes with the measures of all three angles, successfully solving the triangle.

Mindmap
Keywords
💡Law of Cosines
The Law of Cosines is a formula used in geometry to find a side length of a triangle when two sides and the included angle are known. It is a generalization of the Pythagorean theorem and is essential for solving triangles in various scenarios. In the video, the Law of Cosines is applied in multiple forms to find missing sides and angles of triangles given different sets of information.
💡SAS (Side-Angle-Side)
SAS is a method for solving triangles when two sides and the included angle are known. It is one of the scenarios where the Law of Cosines is particularly useful. The video script mentions solving triangles of the form SAS, indicating that the method involves using the known side lengths and angle to find the missing elements of the triangle.
💡SSS (Side-Side-Side)
SSS refers to a triangle solving scenario where all three sides of a triangle are known, and the goal is to find all three angles. The Law of Cosines is also used in this case to determine the angles when the sides are given. The script discusses solving a triangle given all three sides as an example.
💡Cosine
Cosine is a trigonometric function that relates the angle of a right triangle to the ratio of the lengths of its adjacent side to the hypotenuse. In the context of the video, cosine is used in the Law of Cosines formula to find missing sides and angles of triangles.
💡Triangle Angle Sum Theorem
The Triangle Angle Sum Theorem states that the sum of the interior angles of a triangle is always 180 degrees. This theorem is used in the script to find the third angle of a triangle when the other two are known, as seen when calculating angle B after finding angles A and C.
💡Inverse Cosine
Inverse Cosine, also known as arccosine, is the inverse function of the cosine and is used to find the angle when the cosine value is known. In the video, inverse cosine is used to solve for angles when the cosine of those angles, derived from the Law of Cosines, is calculated.
💡Square
To 'square' a number means to multiply the number by itself. In the context of the video, squaring is used in the process of applying the Law of Cosines, where the lengths of sides are squared before being plugged into the formula.
💡Square Root
A square root of a number is a value that, when multiplied by itself, gives the original number. In the script, the square root is used to find the length of a side when its square is known, as seen when calculating side C from C squared.
💡Calculator
A calculator is a device or software used to perform mathematical calculations. In the video script, a calculator is mentioned as the tool used to perform the actual computations required by the Law of Cosines and to find the values of the sides and angles of the triangles.
💡Degrees
Degrees are a unit of measurement used to express angles in a geometric context. In the video, angles are given in degrees, and the Law of Cosines is applied using these degree measurements to find the missing elements of triangles.
💡Plugging In
In the context of the video, 'plugging in' refers to the process of substituting known values into a mathematical formula or equation. This is a common step in solving for unknowns using the Law of Cosines, as demonstrated when the values for sides and angles are substituted into the formula to find the missing side C.
Highlights

Introduction to solving triangles using the Law of Cosines in SAS and SSS scenarios.

Explanation of three forms of the Law of Cosines based on given information.

Demonstration of solving for side C using the formula C^2 = a^2 + b^2 - 2ab*cos(C).

Calculation of side C with given sides a=11, b=5, and angle C=20 degrees.

Use of a calculator to find the approximate value of side C as 6.53.

Finding missing angles in a triangle after determining one side.

Method to isolate the cosine of angle a to find its measure.

Calculation of angle a using the rearranged Law of Cosines formula.

Determination of angle a to be approximately 144.80 degrees.

Process to find angle B using the sum of angles in a triangle equaling 180 degrees.

Calculation of angle B to be approximately 15.20 degrees.

Transition to solving a triangle given all three sides using the Law of Cosines.

Isolation of cosine of angle a to find its measure with sides a=9, b=7, and c=5.

Calculation resulting in angle a being approximately 95.74 degrees.

Finding angle B using a similar process with the Law of Cosines.

Determination of angle B to be approximately 50.70 degrees.

Final calculation of angle C using the sum of angles in a triangle.

Conclusion with angle C being approximately 33.56 degrees.

Completion of the tutorial with a summary of the solved triangle's sides and angles.

Transcripts

Browse More Related Video

How To Calculate The Missing Side Length of a Triangle

Law of Cosines, Finding Angles & Sides, SSS & SAS Triangles - Trigonometry

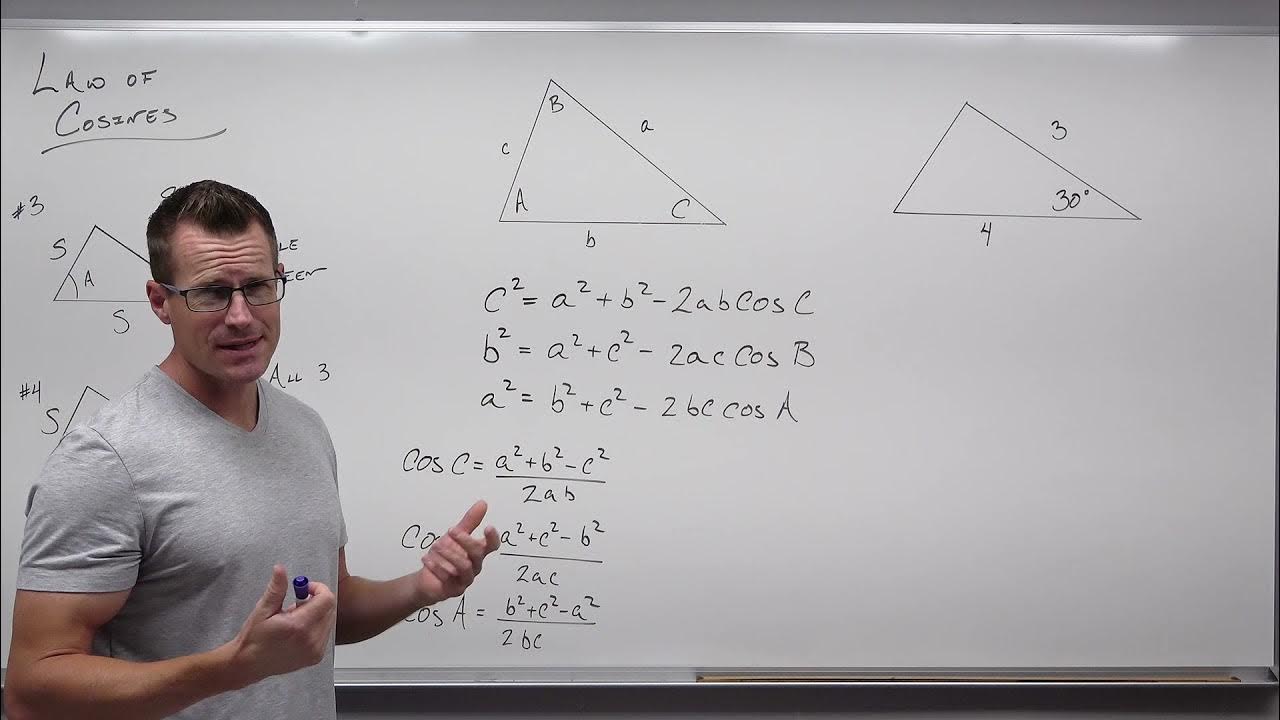
How to Use the Law of Cosines in Trigonometry (Precalculus - Trigonometry 33)

The Law of Cosines

How To Calculate The Missing Angle In a Triangle

Trigonometry - How To Solve Right Triangles

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Triangle SolvingLaw of CosinesMathematicsEducationalSASSSSTrigonometryGeometryProblem SolvingMath Tutorial