How To Calculate The Missing Angle In a Triangle

The Organic Chemistry Tutor
9 Jun 202014:32
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video offers a step-by-step guide on calculating missing angles in triangles, starting with basic examples and progressing to more complex problems. It covers fundamental principles like the sum of angles in a triangle equaling 180 degrees and introduces trigonometric ratios (SOHCAHTOA) for right triangles. The video also explains how to use the law of sines and law of cosines for non-right triangles, highlighting the potential for two solutions in some cases. The presenter ensures clarity by providing multiple examples and emphasizing the importance of checking work for accuracy.

Takeaways
  • 📐 The sum of all angles in a triangle equals 180 degrees.
  • 🔍 To find a missing angle, set up an equation based on the known angles and solve for the unknown.
  • 📈 For a triangle with known angles and sides, use the law of sines or cosines to find unknown angles.
  • 🧭 The law of sines states that the ratio of the length of a side to the sine of its opposite angle is constant for all three sides and angles.
  • 📐 The law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles.
  • 📚 Use trigonometric ratios (SOHCAHTOA) to solve for angles in right triangles.
  • 📉 SOHCAHTOA helps to remember the trigonometric ratios: sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent).
  • 🔢 When using trigonometric functions, ensure your calculator is set to degree mode, not radian mode.
  • 🤔 Consider the possibility of two solutions when using the law of sines, as it can yield an angle and its supplementary angle.
  • 🔄 To check the validity of a solution, ensure that the sum of the angles in the triangle equals 180 degrees.
  • 🔄 For complex problems, use the law of cosines to find one angle, then use the law of sines or angle sum property to find the remaining angles.
Q & A

  • What is the sum of all angles in a triangle?

    -The sum of all angles in a triangle is always 180 degrees.

  • How do you calculate the missing angle in a triangle if you know two angles?

    -You can calculate the missing angle by subtracting the sum of the two known angles from 180 degrees.

  • What is the formula for calculating the sine of an angle in a right triangle?

    -The sine of an angle in a right triangle is calculated as the length of the side opposite the angle divided by the length of the hypotenuse.

  • What trigonometric ratio is used when you have the adjacent side and the hypotenuse of a right triangle?

    -The cosine ratio is used when you have the adjacent side and the hypotenuse of a right triangle.

  • How do you find the missing angle in a non-right triangle using the Law of Sines?

    -You use the Law of Sines to find the missing angle by setting up the equation sin(A)/a = sin(B)/b = sin(C)/c, where A, B, and C are angles and a, b, and c are the sides opposite those angles, respectively.

  • What is the Law of Cosines and how is it used to calculate an angle in a triangle?

    -The Law of Cosines is a formula used to find an angle in a triangle when you know the lengths of all three sides. It is expressed as c² = a² + b² - 2ab*cos(C), where C is the angle opposite side c.

  • Why might you get two possible answers when using the Law of Sines to calculate an angle in a triangle?

    -You might get two possible answers because the Law of Sines can yield an angle and its supplementary angle, which is 180 degrees minus the calculated angle.

  • How do you verify if the two possible angles obtained from the Law of Sines are valid for the triangle?

    -You verify the angles by checking if the sum of the two angles plus the third known angle equals 180 degrees, which is the total sum of angles in a triangle.

  • What is the SOHCAHTOA mnemonic used for in trigonometry?

    -The SOHCAHTOA mnemonic is used to remember the three primary trigonometric ratios: sine (SOH), cosine (CAH), and tangent (TOA), which relate the angles and sides of a right triangle.

  • How do you calculate the cosine of an angle in a right triangle when you have the adjacent side and the hypotenuse?

    -You calculate the cosine of an angle by dividing the length of the adjacent side by the length of the hypotenuse.

  • What is the process for finding the angle in a triangle when you know the lengths of all three sides?

    -You can use the Law of Cosines to find the angle when you know all three sides of the triangle. Rearrange the formula to solve for the cosine of the angle and then use the arc cosine function to find the angle in degrees.

Outlines
00:00
📚 Basic Triangle Angle Calculation

This paragraph introduces the concept of calculating missing angles in triangles. It begins with a simple example where the sum of angles in a triangle is 180 degrees. Given two angles, the third is found by subtraction. The example provided has angles A (30 degrees), B (x), and C (45 degrees), and by adding 30 and 45, we get 75 degrees. Subtracting this from 180 gives angle B (105 degrees). The paragraph then moves on to a more complex problem involving variables, where angles A (44 degrees), B (9x + 10), and C (12x) are given. The solution involves algebraic manipulation to find the value of x, which is then used to determine angles B and C (64 and 72 degrees, respectively). The process is verified by checking that all angles sum to 180 degrees.

05:02
📐 Right Triangle Angle Calculation with Trigonometry

This paragraph discusses how to calculate missing angles in right triangles using trigonometry. The trigonometric ratios sine, cosine, and tangent are introduced with the mnemonic 'sohcahtoa'. The example provided involves a right triangle with a hypotenuse of 15 and an opposite side to angle x of 7. Using the sine ratio, the paragraph demonstrates how to find angle x by taking the inverse sine (arc sine) of the opposite side over the hypotenuse, yielding an angle of 27.8 degrees. Another example follows, where cosine is used to find angle x when the adjacent side and hypotenuse are known, resulting in an angle of 43.3 degrees. The paragraph emphasizes the correct use of trigonometric ratios based on the sides available.

10:02
🧭 Advanced Triangle Angle Calculation Using Law of Sines

The paragraph explores the use of the Law of Sines for calculating angles in non-right triangles. It explains that the Law of Sines relates the ratio of a side to the sine of its opposite angle. The example given has angle A (40 degrees), side a (10), side b (12), and an unknown angle B. The Law of Sines is applied to find the sine of angle B, which is then used to calculate angle B using the inverse sine function, resulting in two possible angles: 50.47 degrees and 129.53 degrees. The paragraph highlights the importance of checking the validity of these angles by ensuring that the sum of angles A and B does not exceed 180 degrees.

📏 Law of Cosines for Angle Calculation in Known Side Triangles

The final paragraph delves into the Law of Cosines for finding an angle in a triangle when all three sides are known. The Law of Cosines is rearranged to solve for angle A, with the formula provided. The example given has sides b (10), a (9), and c (unknown), and the paragraph walks through the calculation of angle A using the rearranged Law of Cosines formula. The result is angle A equal to 58.75 degrees. The paragraph concludes by mentioning that once angle A is found, angle B can be calculated using the Law of Sines, and angle C can be determined by ensuring the sum of all angles equals 180 degrees.

Mindmap
Keywords
💡Missing Angle
The term 'missing angle' refers to an unknown angle in a geometric shape, such as a triangle, where the other angles or sides are known. In the video, the main theme revolves around methods to calculate this unknown angle using various mathematical formulas and properties. It is central to the instructional content as it is the problem the video aims to solve.
💡Sum of Angles in a Triangle
This concept states that the sum of the three interior angles of a triangle always equals 180 degrees. It is a fundamental principle used in the video to solve for the missing angle when two angles are known. The script illustrates this by adding the known angles and subtracting from 180 to find the third.
💡SOHCAHTOA
SOHCAHTOA is a mnemonic for recalling the trigonometric ratios sine, cosine, and tangent in a right triangle. It stands for 'Sine is Opposite over Hypotenuse, Cosine is Adjacent over Hypotenuse, Tangent is Opposite over Adjacent.' In the context of the video, this mnemonic is used to calculate the missing angle in a right triangle when the lengths of two sides are known.
💡Law of Sines
The Law of Sines is a formula that relates the lengths of sides of a triangle to the sines of its angles. It is expressed as \( \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c} \). In the video, the Law of Sines is used to find an angle when the lengths of two sides and one angle (other than the right angle) of a triangle are known.
💡Law of Cosines
The Law of Cosines is a formula used to find an angle or a side in a triangle when certain other sides and angles are known. It is given by \( c^2 = a^2 + b^2 - 2ab \cdot \cos(C) \). In the video, this law is rearranged to solve for an unknown angle when the lengths of all three sides of a triangle are known.
💡Arc Sine (sin^-1)
The arc sine function, denoted as sin^-1 or arcsin, is the inverse function of the sine. It is used to find an angle when the sine of that angle is known. In the video, the arc sine is used to calculate the measure of an angle in a right triangle after finding the ratio of the opposite side to the hypotenuse.
💡Arc Cosine (cos^-1)
Similar to arc sine, the arc cosine function, denoted as cos^-1 or arccos, is the inverse of the cosine function. It is used in the video to find an angle in a right triangle when the adjacent side and the hypotenuse are known, by calculating the cosine of the angle and then finding its inverse.
💡Hypotenuse
The hypotenuse is the longest side of a right triangle, opposite the right angle. It plays a crucial role in trigonometric calculations, especially when using SOHCAHTOA ratios. In the video, the hypotenuse is used as one of the known sides to calculate the missing angle using sine, cosine, or tangent.
💡Trigonometric Ratios
Trigonometric ratios, such as sine, cosine, and tangent, are ratios of the sides of a right triangle that relate to its angles. They are essential in solving for missing angles or sides in a triangle. The video explains how to apply these ratios using the mnemonic SOHCAHTOA to find missing angles in various scenarios.
💡Inverse Trigonometric Functions
Inverse trigonometric functions, such as arcsine and arccosine, are used to find the angle when the trigonometric ratio is known. They are the inverse operations of the standard trigonometric functions. The video demonstrates the use of these functions to calculate the measure of angles when the corresponding trigonometric ratios are given.
💡Calculator Mode
The video script mentions the need to ensure that a calculator is in degree mode rather than radian mode when performing trigonometric calculations. This is important because the results of trigonometric functions vary depending on whether the input is in degrees or radians, affecting the accuracy of the calculated angles.
Highlights

The video explains how to calculate the missing angle of a triangle using various methods.

Triangles have the property that the sum of their three angles equals 180 degrees.

A simple example shows how to find angle B (or x) when given angle A and angle C.

The process involves isolating the unknown angle and then solving for it.

For a more complex problem, the video introduces variables and algebraic manipulation to find the angles.

The value of x is found by solving an equation involving the sum of angles in a triangle.

The video demonstrates how to calculate the measures of angles B and C using algebraic expressions.

Checking the work is crucial by ensuring that the sum of the calculated angles equals 180 degrees.

In a right triangle, the video explains the use of trigonometric ratios (SOHCAHTOA) to find an angle.

The sine, cosine, and tangent ratios are introduced for solving right triangle problems.

The video shows how to use the sine function to find an angle when the opposite side and hypotenuse are known.

The arc sine function on a calculator is used to find the measure of angle x in a right triangle.

The law of sines is introduced for non-right triangles when two sides and an angle (not included) are known.

The video demonstrates solving for an angle using the law of sines and finding multiple possible solutions.

The law of cosines is presented for finding an angle when all three sides of a triangle are known.

The rearrangement of the law of cosines formula is shown to solve for a specific angle.

The video concludes with an example of using the law of cosines to find angle A and subsequently angle B and C.

The importance of checking the sum of angles to ensure a valid triangle is emphasized.

The video provides a comprehensive guide on triangle angle calculations for various types of triangles.

Transcripts

Browse More Related Video

How To Calculate The Missing Side Length of a Triangle

How to Use the Law of Sines in Trigonometry (Precalculus - Trigonometry 32)

Law of Sines, Basic Introduction, AAS & SSA - One Solution, Two Solutions vs No Solution, Trigonomet

Trigonometry - How To Solve Right Triangles

Law of Sines - Basic Introduction

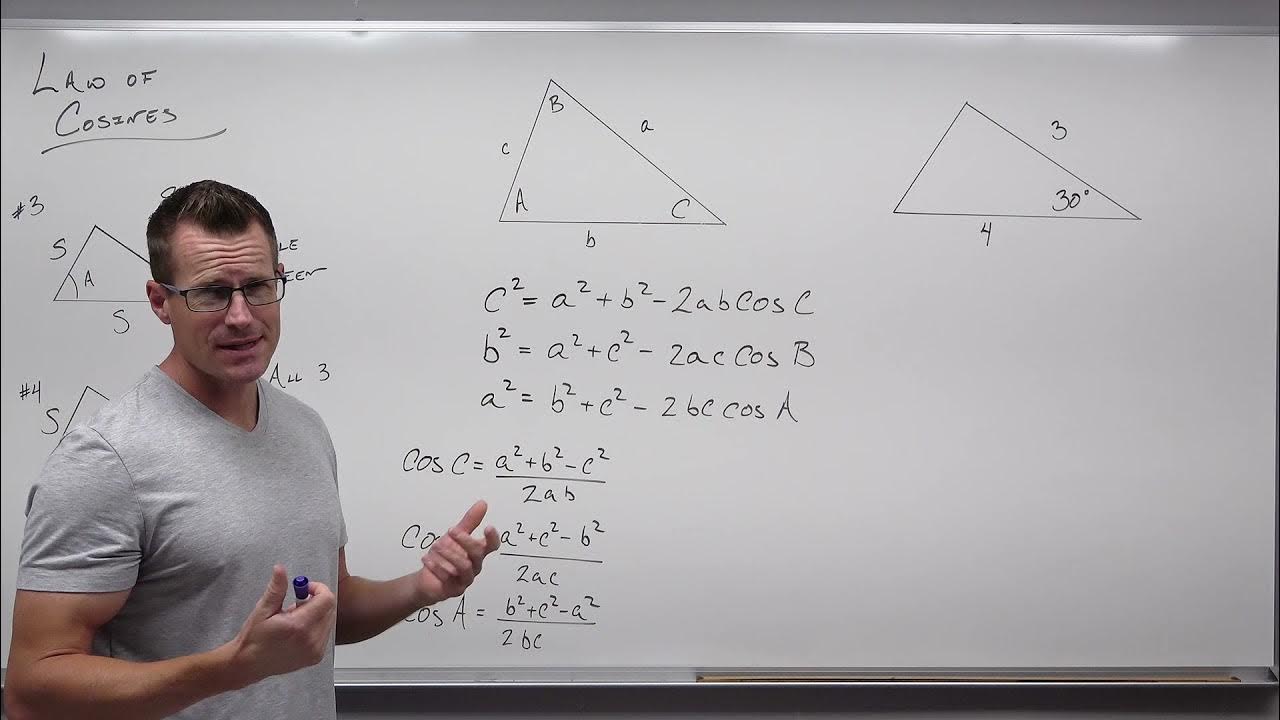
How to Use the Law of Cosines in Trigonometry (Precalculus - Trigonometry 33)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Triangle AnglesMathematicsCalculusGeometryTrigonometrySohCahToaLaw of SinesLaw of CosinesEducational VideoProblem Solving