Integration in Spherical Coordinates

Dr. Trefor Bazett
15 Dec 201907:51
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial explores the concept of spherical coordinates, demonstrating how to convert between Cartesian and spherical coordinates using rho, phi, and theta. It visually illustrates defining a region in spherical coordinates, resembling a section of an ice cream cone, and explains the process of integrating functions over such regions. The video concludes with a practical example of calculating the volume of a geometric shape using triple integrals with respect to the differential volume element rho squared sine phi d rho d phi d theta.

Takeaways
  • 📐 Spherical coordinates are an alternative system to Cartesian coordinates, using a radius (rho), a polar angle (phi), and an azimuthal angle (theta).
  • 📍 The radius (rho) is the distance from the origin to a point in space, similar to the radial distance in polar coordinates.
  • 📊 The polar angle (phi) is the angle between the line from the origin to the point and the positive z-axis.
  • 📉 The azimuthal angle (theta) is the angle between the projection of the line onto the xy-plane and the positive x-axis.
  • 🔄 Conversion from spherical to Cartesian coordinates is possible using the formulas: x = rho * sin(phi) * cos(theta), y = rho * sin(phi) * sin(theta), and z = rho * cos(phi).
  • 🔄 The reverse conversion from Cartesian to spherical coordinates can also be done, allowing for the analysis of regions in space defined by spherical coordinates.
  • 🍦 The script uses the analogy of an 'ice cream cone' to visualize a region in spherical coordinates, with the top being a spherical cap and the base a 'comb' shape.
  • 📏 The region's boundaries are defined by specific ranges for rho, phi, and theta, which restrict the area to a particular section of the spherical coordinate system.
  • ∫ The script introduces the concept of integrating functions over regions in spherical coordinates, with the integral involving the differential volume element rho^2 * sin(phi) * dRho * dPhi * dTheta.
  • 📚 The volume of a region, such as the 'ice cream cone' example, can be calculated using a triple integral with the appropriate limits for rho, phi, and theta.
  • 📈 Understanding the geometry behind the differential volume element in spherical coordinates is crucial for correctly setting up and evaluating integrals.
  • 👨‍🏫 The video script is part of a larger series on multivariable calculus, suggesting further exploration of these concepts for those interested.
Q & A

  • What are spherical coordinates?

    -Spherical coordinates are a three-dimensional coordinate system that uses three values to specify a point in space relative to an origin: the radial distance (ρ) from the origin, the polar angle (θ) from the positive z-axis, and the azimuthal angle (φ) from the positive x-axis in the xy-plane.

  • How is the radial distance (ρ) defined in spherical coordinates?

    -The radial distance (ρ) is the straight-line distance from the origin to the point in space, similar to the r in polar coordinates.

  • What is the polar angle (θ) in spherical coordinates?

    -The polar angle (θ) is the angle between the line from the origin to the point and the positive z-axis, ranging from 0 to π radians.

  • How is the azimuthal angle (φ) related to the xy-plane in spherical coordinates?

    -The azimuthal angle (φ) is the angle between the projection of the line from the origin to the point onto the xy-plane and the positive x-axis, ranging from 0 to 2π radians.

  • What is the relationship between spherical coordinates and Cartesian coordinates?

    -Spherical coordinates can be converted to Cartesian coordinates using the equations x = ρ * sin(θ) * cos(φ), y = ρ * sin(θ) * sin(φ), and z = ρ * cos(θ).

  • How can you describe a region in spherical coordinates?

    -A region in spherical coordinates can be described by specifying intervals for ρ, θ, and φ that correspond to the boundaries of the region in the three-dimensional space.

  • What is the significance of the triple integral in spherical coordinates?

    -The triple integral in spherical coordinates is used to integrate functions over a region in three-dimensional space, taking into account the volume element dV, which is ρ² * sin(φ) dρ dφ dθ in spherical coordinates.

  • How can you find the volume of a region described in spherical coordinates?

    -To find the volume, you integrate the function f(ρ, φ, θ) = 1 over the specified region with the volume element dV, using the limits for ρ, θ, and φ that define the region.

  • What is the volume element dV in spherical coordinates?

    -The volume element dV in spherical coordinates is ρ² * sin(φ) dρ dφ dθ, which accounts for the infinitesimal volume in the three-dimensional space.

  • Can you provide an example of a region described in spherical coordinates from the script?

    -An example from the script is a region that resembles a portion of an ice cream cone, defined by ρ = 1, θ between 0 and π/6, and φ between 0 and 3π/2.

  • How does the script describe the process of integrating a function over a region in spherical coordinates?

    -The script describes the process by first identifying the function to be integrated, then specifying the limits of integration for ρ, θ, and φ that correspond to the region, and finally calculating the triple integral with the volume element dV.

Outlines
00:00
📚 Introduction to Spherical Coordinates

This paragraph introduces the concept of spherical coordinates as an alternative to Cartesian coordinates. It explains how to define a point in space using three parameters: the radial distance (Rho) from the origin to the point, the polar angle (Phi) between the z-axis and the line connecting the origin to the point, and the azimuthal angle (Theta) between the positive x-axis and the projection of this line onto the xy-plane. The explanation includes how to convert between spherical and Cartesian coordinates using trigonometric relationships.

05:01
🍦 Visualizing Regions in Spherical Coordinates

The second paragraph delves into visualizing a specific region in spherical coordinates, likened to a portion of an ice cream cone. The region is defined by constraints on Rho, Phi, and Theta. Rho is restricted to a value of one, representing a sphere with a radius of one. Phi is limited to the range between 0 and pi/6, indicating a section from the z-axis up to a certain angle. Theta is confined to the range between 0 and 3pi/2, which corresponds to three-quarters of a circle in the xy-plane. This visualization helps in understanding how regions can be described in spherical coordinates.

🧮 Integrating Functions in Spherical Coordinates

This paragraph discusses the process of integrating functions over regions defined in spherical coordinates. It starts by describing the triple integral of a function in terms of the differential volume element in spherical coordinates, which is given by Rho squared sine Phi dRho dPhi dTheta. The paragraph then provides an example of calculating the volume of the previously described 'ice cream cone' region by integrating the constant function one over the specified limits of integration for Rho, Phi, and Theta. This demonstrates how to apply the principles of integration in spherical coordinates to find volumes of complex regions.

Mindmap
Keywords
💡Spherical Coordinates
Spherical coordinates are a three-dimensional coordinate system that specifies points in space using three values: the radial distance from the origin (Rho), the polar angle (Phi) from the positive z-axis, and the azimuthal angle (Theta) in the xy-plane from the positive x-axis. In the video, spherical coordinates are used to define and visualize regions in space, such as the 'ice cream cone' example, and to perform integration over these regions.
💡Cartesian Coordinates
Cartesian coordinates are a two-dimensional or three-dimensional coordinate system that specifies points in space using x, y, and z values. The video begins with a point in Cartesian coordinates and then explains how to convert these to spherical coordinates, which is essential for understanding the transition from the familiar Cartesian system to the less intuitive spherical system.
💡Rho (ρ)
Rho, symbolized by the Greek letter ρ, is the radial distance from the origin to a point in spherical coordinates. It is analogous to the radius in polar coordinates. In the video, Rho is used to define the distance from the origin to various points, such as the top of the 'ice cream cone' region, which is constrained by Rho being equal to one.
💡Phi (φ)
Phi, symbolized by the Greek letter φ, is the polar angle in spherical coordinates, measured from the positive z-axis. It is used in the video to define the angle constraints of the 'ice cream cone' region, which is limited to values between 0 and pi/6, indicating the vertical extent of the region from the z-axis.
💡Theta (θ)
Theta, symbolized by the Greek letter θ, is the azimuthal angle in spherical coordinates, measured in the xy-plane from the positive x-axis. The video uses Theta to describe the angular extent of the region in the xy-plane, which is limited to values between 0 and 3pi/2, representing three-quarters of a full circle.
💡Integration
Integration in the context of the video refers to the process of calculating the volume or other properties of a region in space by summing up an infinitesimal quantity over that region. The video demonstrates how to perform a triple integral over a region defined in spherical coordinates to find the volume of the 'ice cream cone' region.
💡Volume
Volume is a measure of the amount of space occupied by a three-dimensional region. In the video, the concept of volume is central to the example of finding the volume of a specific region in spherical coordinates, which is visualized as an 'ice cream cone' with a spherical top and a comb base.
💡Polar Coordinates
Polar coordinates are a two-dimensional coordinate system in which each point is determined by a radius from a fixed point and an angle from a fixed direction. The video mentions polar coordinates when explaining the transition from Cartesian to spherical coordinates and when discussing the conversion between the x and y components and the radial and angular components in spherical coordinates.
💡Trigonometry
Trigonometry is the branch of mathematics that deals with the relationships between the sides and angles of triangles, particularly right-angled triangles. In the video, trigonometry is used to relate the Cartesian coordinates to the spherical coordinates through the use of sine and cosine functions, which are essential for determining the x, y, and z components from Rho, Phi, and Theta.
💡Differential Element (dV)
The differential element dV in the video represents an infinitesimal volume element in three-dimensional space over which the function is being integrated. The video explains that in spherical coordinates, the differential volume element is given by Rho squared times the sine of Phi times dRho times dPhi times dTheta, which is crucial for setting up the integral to find the volume of a region.
Highlights

Introduction to the concept of spherical coordinates and their use in defining circle coordinates.

Explanation of converting Cartesian coordinates to spherical coordinates using rho, phi, and theta.

Rho is defined as the distance from the origin to the point, similar to the radial distance in polar coordinates.

Phi is the angle between the line from the origin to the point and the z-axis.

Theta is the angle in the XY plane between the positive x-axis and the projection of the line from the origin to the point.

Conversion formulas from spherical to Cartesian coordinates are presented.

Visualization of a region in spherical coordinates, described as a portion of an 'ice cream cone'.

Description of the rho, phi, and theta values that define the boundaries of the 'ice cream cone' region.

Integration of functions over regions in spherical coordinates and the importance of the differential volume element.

The differential volume element in spherical coordinates is rho squared sine phi d rho d phi d theta.

Method to find the volume of a region described in spherical coordinates through triple integration.

Example of calculating the volume of a specific 'ice cream cone' region with a spherical top and a comb base.

Integration limits for rho, phi, and theta are defined for the given region.

The volume calculation involves integrating the function one over the specified intervals.

Encouragement for viewers to leave comments with questions about the video content.

Invitation to like the video and subscribe for more multivariable calculus content.

Reference to a larger playlist of multivariable calculus videos for further learning.

Transcripts

Browse More Related Video

Calculus 3: Triple Integrals in Spherical Coordinates (Video #25) | Math with Professor V

Triple Integrals in Spherical Coordinates

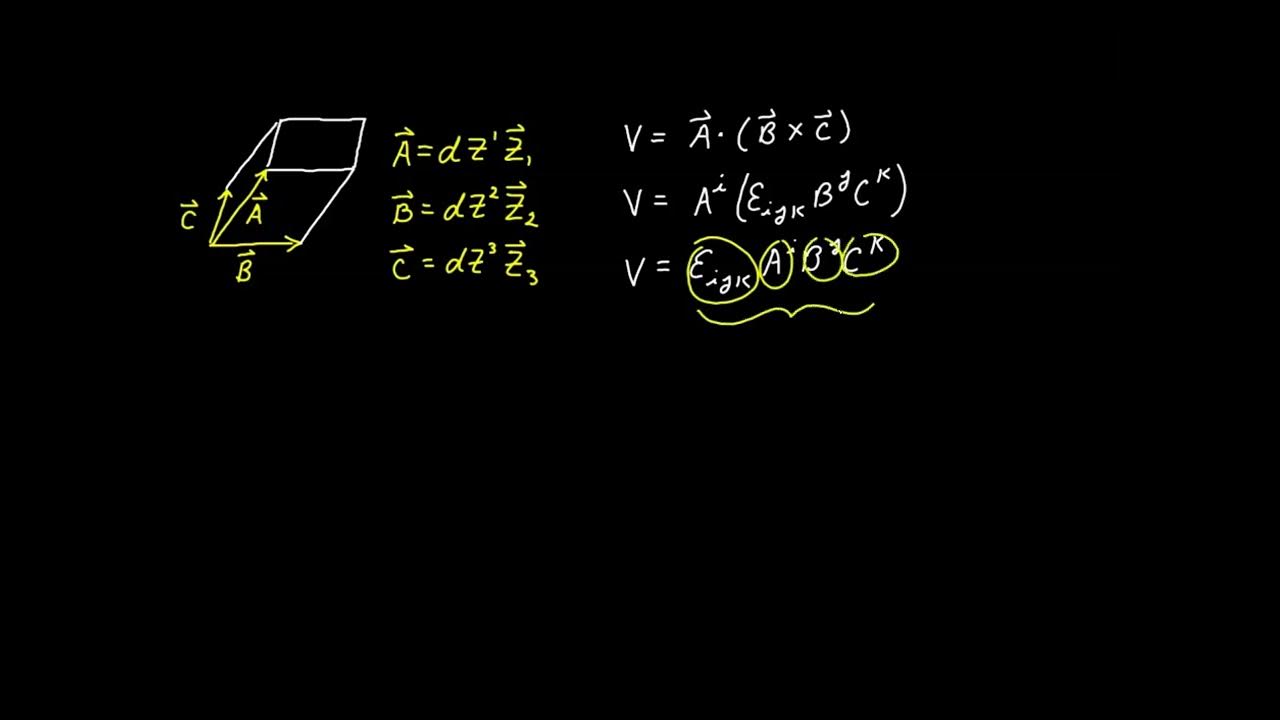
Video 54 - Integration

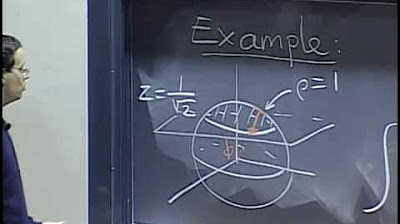
Lec 26: Spherical coordinates; surface area | MIT 18.02 Multivariable Calculus, Fall 2007

Double Integration in Polar Coordinates | Example & Derivation

Double Integrals in Polar Coordinates

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Spherical CoordinatesMathematics TutorialIntegrationCartesian ConversionMultivariable CalculusPolar to SphericalVolume CalculationTrigonometryGeometryEducational Content