Triple Integrals in Spherical Coordinates

Houston Math Prep

26 Apr 202028:42

EducationalLearning

32 Likes 10 Comments

TLDRThis video from Houston Math Prep offers an in-depth tutorial on spherical coordinates, essential for advanced calculus students. It covers the basics of spherical coordinates, including the conversion from rectangular coordinates, and delves into setting up triple integrals in spherical coordinates. The instructor demonstrates how to evaluate these integrals with several examples, including calculating the mass of a sphere and the volume of complex 3D regions, such as a cone intersecting with a plane. The video is a valuable resource for those mastering multivariable calculus.

Takeaways

📚 The video is a tutorial on spherical coordinates, focusing on their basics, conversions from rectangular coordinates, and setting up triple integrals in spherical coordinates.
📐 Spherical coordinates are represented by the variables rho (ρ), phi (φ), and theta (θ), where rho is the distance from the origin, phi is the angle from the positive z-axis, and theta is the polar angle in the xy-plane.
🔄 Conversion formulas between rectangular (x, y, z) and spherical coordinates are provided, using the relationships involving rho, phi, and theta to convert between the two systems.
🌍 The equation of a sphere centered at the origin is given by x^2 + y^2 + z^2 = rho^2, which is foundational for understanding the geometry of spherical coordinates.
📦 The unit of volume in spherical coordinates is derived, which is essential for setting up triple integrals to calculate volumes, masses, or other scalar quantities within a 3D region.
∫ The formula for the unit of volume in spherical coordinates is given as rho^2 * sin(phi) * d(rho) * d(phi) * d(theta), which is used in triple integrals.
🌀 An example of calculating the mass of a sphere with a density function dependent on rho, phi, and theta is demonstrated using a triple integral.
📘 The process of setting up and evaluating a triple integral for the mass of a sphere, including determining the bounds for rho, phi, and theta, is explained step by step.
📊 The video provides examples of calculating volumes for regions within a cone and a sphere, and above a cone with a flat top, using triple integrals in spherical coordinates.
📌 The importance of correctly identifying the bounds for each variable (rho, phi, theta) in the triple integral based on the geometry of the region of interest is emphasized.
🎓 The tutorial concludes by highlighting the complexity of multiple integrals and encourages viewers to consult calculus textbooks or online resources for a deeper understanding of the concepts.

Q & A

What are the three variables used in spherical coordinates?
-In spherical coordinates, the three variables used are Rho (ρ), Phi (φ), and Theta (θ).
How is Rho (ρ) defined in spherical coordinates?
-Rho (ρ) in spherical coordinates is defined as the distance from the origin to the point in 3D space.
What is the relationship between the angle Phi (φ) and the z-axis in spherical coordinates?
-Phi (φ) is the angle measured downward from the positive z-axis.
What is the role of Theta (θ) in spherical coordinates?
-Theta (θ) is the polar angle measured in the XY plane, counterclockwise when viewed from above.
How can you convert from rectangular coordinates to spherical coordinates?
-You can convert from rectangular to spherical coordinates using the formulas: ρ = √(x² + y² + z²), φ = arccos(Z/ρ), and θ = arctan(y/x), considering x ≥ 0.
What is the equation of a sphere centered at the origin in terms of spherical coordinates?
-The equation of a sphere centered at the origin in terms of spherical coordinates is x² + y² + z² = ρ².
What is the unit of volume in spherical coordinates?
-The unit of volume in spherical coordinates is given by the expression ρ² * sin(φ) * dρ * dφ * dθ.
How is the volume of a region in 3D space calculated using spherical coordinates?
-The volume of a region in 3D space is calculated using a triple integral with the unit of volume in spherical coordinates, which is ρ² * sin(φ) * dρ * dφ * dθ.
What is the process of setting up a triple integral to find the mass of an object with a density function in spherical coordinates?
-To find the mass, you set up a triple integral with the density function multiplied by the unit of volume in spherical coordinates and integrate over the appropriate bounds for ρ, φ, and θ.
Can you provide an example of calculating the mass of a sphere with a given density function using spherical coordinates?
-Yes, for a sphere of radius four with a density function f(ρ, φ, θ) = 5 - ρ, the mass is calculated by the triple integral ∫(0 to 2π)∫(0 to π)∫(0 to 4) [(5 - ρ) * ρ² * sin(φ) * dρ * dφ * dθ].
What is the volume of a cone with an angle of V = π/3 and inside a sphere with Rho = 6?
-The volume of the region between the cone V = π/3 and the sphere Rho = 6 is calculated by the triple integral with bounds for ρ from 0 to 6, for φ from 0 to π/3, and for θ from 0 to 2π, using the unit of volume in spherical coordinates.
How do you find the volume of a region bounded by a cone and a flat plane in spherical coordinates?
-You set up a triple integral with the unit of volume in spherical coordinates and determine the bounds for ρ (from 0 to 3 secant(φ)), for φ (from 0 to π/3), and for θ (from 0 to 2π), then integrate to find the volume.

Outlines

00:00

📚 Introduction to Spherical Coordinates and Basic Conversions

The video begins with an introduction to spherical coordinates, explaining the variables involved: Rho (ρ), Phi (φ), and Theta (θ). Rho represents the distance from the origin to a point in 3D space, Phi is the angle measured downward from the positive z-axis, and Theta is the polar angle in the xy-plane. The script discusses the conversion from rectangular to spherical coordinates using geometric interpretations and trigonometric relationships. The equation of a sphere, x² + y² + z² = ρ², is introduced as the foundational equation for understanding spherical coordinates.

05:01

📐 Setting Up Triple Integrals in Spherical Coordinates

The script moves on to set up triple integrals in spherical coordinates, focusing on the unit of volume in this coordinate system. It explains that the volume element in spherical coordinates is given by dV = ρ² sin(φ) dρ dφ dθ, which accounts for the 'rounded' nature of the volume element. The video emphasizes the importance of understanding this volume element when performing triple integrals to calculate volumes or masses in spherical coordinates.

10:01

🔍 Example: Mass of a Sphere with Variable Density

An example is presented to calculate the mass of a sphere with radius four and a density function dependent on Rho (ρ), Phi (φ), and Theta (θ). The density function is given as five minus Rho (5 - ρ). The video demonstrates setting up the triple integral for mass, integrating over the appropriate bounds for ρ, φ, and θ, and simplifying the expression to find the total mass of the sphere.

15:02

📏 Example: Volume Between a Cone and a Sphere

The script explores the calculation of the volume enclosed by a cone with an apex angle of π/3 and a sphere with radius 6. The triple integral for volume is set up without a density function, and the bounds for ρ, φ, and θ are determined based on the geometry of the intersection between the cone and the sphere. The integration process is outlined, leading to the calculation of the volume.

20:03

📘 Example: Volume Under a Plane and Above a Cone

This paragraph delves into a more complex scenario where the volume under a plane z = 3 and above a cone with an apex angle of π/3 is calculated. The video explains how to determine the bounds for ρ in terms of the secant of φ, and how to integrate over the bounds for φ and θ. The process involves trigonometric identities and substitutions to simplify the integral and find the volume.

25:04

🎓 Conclusion and Encouragement for Advanced Integration

The video concludes with a summary of the process for setting up and solving triple integrals in spherical coordinates, highlighting the importance of understanding the unit of volume and the geometric interpretation of the bounds. It encourages viewers who have reached this point in their study of multiple integration to continue their efforts, as they are nearing the completion of the topic in calculus.

Mindmap

Keywords

💡Spherical Coordinates

Spherical coordinates are a three-dimensional coordinate system that specifies points in terms of radial distance, polar angle, and azimuthal angle. In the context of the video, spherical coordinates are used to describe the position of a point in 3D space relative to the origin, with 'Rho' representing the radial distance, 'Phi' the angle from the positive z-axis, and 'Theta' the polar angle in the xy-plane. The video explains the conversion from rectangular to spherical coordinates and their use in setting up triple integrals.

💡Rho (ρ)

Rho, represented by the Greek letter, is the radial coordinate in spherical coordinates that measures the distance of a point from the origin in 3D space. The script uses Rho to explain the conversion formulas from rectangular to spherical coordinates and in the calculation of triple integrals, emphasizing its role in determining the magnitude of a point's position in space.

💡Phi (φ)

Phi is the azimuthal angle in spherical coordinates, which represents the angle measured downward from the positive z-axis. The script discusses Phi in the context of forming right triangles that help in converting between coordinate systems and in the calculation of volume and mass within specific regions of 3D space.

💡Theta (θ)

Theta is the polar angle in spherical coordinates, measured counterclockwise in the xy-plane from the positive x-axis. The video script uses Theta to describe the conversion from rectangular to spherical coordinates and in the process of evaluating triple integrals, highlighting its importance in determining the orientation of a point in the horizontal plane.

💡Triple Integrals

Triple integrals are a type of integral used in calculus to calculate volumes, mass, or other properties of three-dimensional regions. The script introduces triple integrals in spherical coordinates, demonstrating how to set up and evaluate them with examples, including the mass of a sphere and the volume of regions bounded by cones and planes.

💡Conversion Formulas

Conversion formulas are mathematical expressions that relate the coordinates of one system to another. The script provides formulas to convert between rectangular (x, y, z) and spherical (Rho, Phi, Theta) coordinates, which are essential for solving problems in physics and engineering that require a change in perspective from Cartesian to a more geometrically intuitive system.

💡Unit of Volume

In the context of triple integrals, the unit of volume refers to the infinitesimal volume element in a given coordinate system. The script explains that in spherical coordinates, the unit of volume is given by the product of Delta Rho, Rho, Delta Phi, and Rho sine Phi times Delta Theta, which is used to calculate the volume of a region in 3D space.

💡Density Function

A density function is a mathematical expression that gives the density of a substance at a point in space. In the script, the density function is used in the context of calculating the mass of a sphere with a variable density that depends on Rho, illustrating how physical properties can be integrated over a region to find total quantities.

💡Cone

A cone is a geometric shape that tapers smoothly from a flat, round base to a point called the apex. The script discusses the volume calculation of a region inside a cone defined by the angle Phi equals PI/3, showing how to set up the bounds for the triple integral in spherical coordinates to find the volume of such a shape.

💡Integration Bounds

Integration bounds define the limits within which an integral is evaluated. The video script explains how to determine the bounds for the variables Rho, Phi, and Theta when setting up triple integrals in spherical coordinates for different regions, such as a sphere, a cone, and a region bounded by a plane and a cone.

💡Secant

Secant is a trigonometric function defined as the reciprocal of the cosine function. In the script, secant is used in the context of finding the bounds for Rho when integrating over a region bounded by a plane and a cone, demonstrating the application of trigonometric identities in solving integrals.

Highlights

Introduction to spherical coordinates and their basic concepts.

Explanation of the variables in spherical coordinates: Rho, Phi, and Theta.

Conversion formulas from rectangular to spherical coordinates and vice versa.

Derivation of the basic equation of a sphere centered at the origin.

Conversion of the vertical component Z in spherical coordinates using trigonometric relations.

Conversion of the horizontal components X and Y using Rho, Phi, and Theta.

Description of the unit of volume in spherical coordinates and its significance in triple integrals.

Calculation of the volume of a sphere using triple integrals in spherical coordinates.

Integration setup for calculating the mass of a sphere with a given density function.

Use of trigonometric identities to simplify the integration process.

Finding the volume inside a cone and a sphere using spherical coordinates.

Setting up triple integral bounds for regions defined by a cone and a plane.

Use of trigonometric relationships to determine bounds for Rho in integrals involving a plane.

Application of u-substitution with tangent function to simplify integrals in spherical coordinates.

Final calculation of the volume under a plane and above a cone using spherical coordinates.

Conclusion and encouragement for viewers nearing the end of their study on multiple integrals.

Transcripts

Browse More Related Video

Calculus 3: Triple Integrals in Spherical Coordinates (Video #25) | Math with Professor V

Triple Integrals in Cylindrical Coordinates

Double Integrals in Polar Coordinates

Integration in Spherical Coordinates

Triple Integrals in Rectangular Coordinates

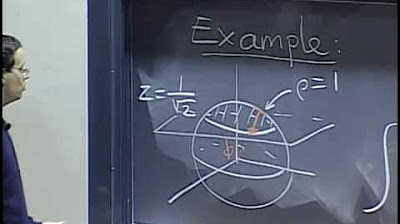
Lec 26: Spherical coordinates; surface area | MIT 18.02 Multivariable Calculus, Fall 2007

Related Tags

Spherical Coordinates Triple Integrals Mathematics Tutorial 3D Geometry Conversion Formulas Volume Calculation Density Function Calculus Techniques Educational Content Advanced Math