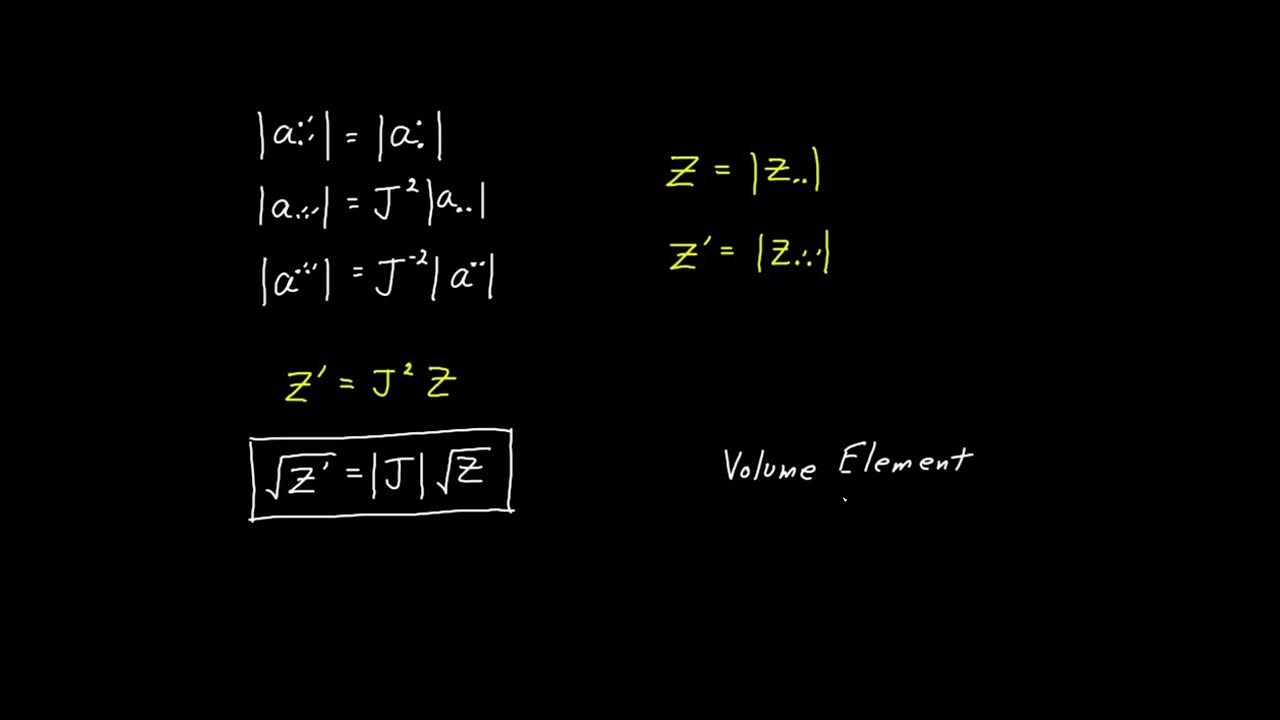Video 54 - Integration
TLDRThis video delves into the concept of a physical integral in tensor calculus, illustrating how to calculate the mass of an object by integrating its density over a volume. It introduces the physical domain, represented by Greek letter omega, and the density function, denoted by rho. The video demonstrates the use of Cartesian coordinates for multiple integrals and emphasizes the importance of choosing correct limits. It then transitions to tensor calculus, deriving an invariant expression for volume differentials that works across all coordinate systems, including spherical polar coordinates, which simplifies the calculation of a sphere's volume. The video concludes by highlighting the strategy of selecting the appropriate coordinate system to simplify physical integral evaluations.
Takeaways
- 📚 The video discusses the concept of a physical integral, which is used to calculate properties like mass of an object based on its density and volume.
- 📏 The physical domain (denoted by Greek letter omega) represents the shape and dimensions of the object for which properties are being calculated.
- 🌌 Density (represented by rho) is a scalar function that varies with position within the physical domain and is essential for calculating mass.
- 🔍 The mass of an object is calculated by integrating the product of density and volume differential over the entire physical domain.
- 📈 Physical integrals are applicable in various physics applications, including total charge, center of mass, and moment of inertia calculations.
- 🌐 The physical integral is independent of the coordinate system used, emphasizing its geometric nature.
- 📝 In Cartesian coordinates, the density function is represented as a function of x, y, and z, and the mass is evaluated using a triple integral with appropriate limits.
- 📉 The limits of integration must be carefully chosen to match the boundaries of the physical domain, which can be challenging.
- 📊 Tensor calculus allows for the derivation of an invariant expression for the volume differential that works with any coordinate system.
- 📐 The volume element, represented by the square root of the metric tensor (√g), acts as a conversion factor ensuring the volume differential remains invariant across coordinate systems.
- 🌕 An example of calculating the volume of a sphere is provided, demonstrating the advantage of choosing the appropriate coordinate system (spherical polar coordinates) for simplicity.
Q & A
What is the main concept explored in this video?
-The main concept explored in this video is the physical integral and how to evaluate it using multiple integrals in any coordinate system.
What is the physical domain in the context of this video?
-The physical domain, represented by the Greek letter omega, refers to the shape, boundary, and dimensions of an object for which properties like mass are being calculated.
What is meant by the density in the context of calculating mass?
-Density, represented by the Greek letter rho, is the mass of an object per unit volume and is a scalar function that can vary with position within the physical domain.
What is a volume differential and how is it used in the context of mass calculation?
-A volume differential, denoted as 'd omega', is an infinitesimal volume element at a specific point within the physical domain. It is used to calculate the mass of that small volume by multiplying it with the density at that point.
What is a physical integral and how does it relate to the mass of an object?
-A physical integral is the integral of a function, such as density, with respect to volume differential over the entire physical domain. It is used to calculate the total mass of an object by summing the products of density and volume differential at every point in the domain.
Why is the coordinate system important for evaluating physical integrals?
-The coordinate system is important for evaluating physical integrals because it provides a framework to perform the actual calculations by defining the limits of integration and the form of the density function with respect to the coordinates.
What is the difference between a physical integral and a mathematical integral?
-A physical integral is specific to the integration of a function over a physical domain with respect to a volume differential, often used in physics to calculate properties like mass. A mathematical integral is a broader concept that can involve the integration of scalar, vector, or tensor functions over any domain.
What is a repeat arithmetic integral or multiple integral?
-A repeat arithmetic integral or multiple integral is a process of integrating a function with respect to one variable at a time, holding the others constant, and is used to evaluate integrals in multiple dimensions, such as in Cartesian coordinates.
What is the significance of the square root of z in tensor calculus?
-In tensor calculus, the square root of z, often referred to as the volume element, is a conversion factor that ensures the volume differential expression remains invariant under different coordinate systems.
How does the video demonstrate the evaluation of a physical integral using spherical polar coordinates?
-The video demonstrates the evaluation of a physical integral using spherical polar coordinates by calculating the volume of a sphere. It shows the simplification of the volume differential and the ease of applying limits in spherical coordinates, leading to a straightforward integration process.
What strategy does the video suggest for choosing a coordinate system when evaluating physical integrals?
-The video suggests avoiding commitment to a specific coordinate system as long as possible and, when necessary, choosing the one that simplifies the problem the most, such as spherical polar coordinates for calculating the volume of a sphere.
Outlines
🔢 Understanding the Concept of Physical Integrals
In this video, which is the 54th in the series on tensor calculus, we explore the concept of a physical integral. The discussion begins by considering the calculation of an object's mass, which requires understanding the shape and boundary of the object, termed the physical domain (represented by the Greek letter omega), and its density (represented by the Greek letter rho). The density is a scalar function that varies with position within the domain. By multiplying a small volume element (differential) with the density at a given point, one obtains the mass of that volume element. Integrating this across the entire physical domain gives the total mass of the object. This type of integration is termed a physical integral, and it can be scalar, vector, or tensor in nature, with applications in calculating total charge, center of mass, and moment of inertia. Notably, a physical integral is independent of any specific coordinate system, emphasizing its geometric nature. However, to evaluate such integrals practically, a coordinate system, like the Cartesian system, is typically used.
📈 Evaluating Mass with Cartesian Coordinates
The video continues to explain how to evaluate the mass of an object using Cartesian coordinates. In this system, the density function is expressed in terms of x, y, and z coordinates. The integration process involves three steps, where the density function is first integrated with respect to x, treating y and z as constants, and then with respect to y and finally z. The limits of these integrations are functions of the remaining variables, ensuring that they accurately represent the physical domain's boundaries. This method of integration is a multiple integral, a fundamental concept in calculus that requires careful selection of limits. The process is not confined to Cartesian coordinates, which leads to exploring other coordinate systems to derive an expression that is invariant across systems.
🔧 Deriving an Invariant Expression for Volume
To illustrate the flexibility of tensor calculus, the video derives an invariant expression for volume using vectors and their components relative to a basis vector system. The vectors, labeled as a, b, and c, point in the directions of basis vectors z1, z2, and z3, respectively, forming a parallelepiped when drawn together. The volume of this parallelepiped is determined using the dot product of vector a with the cross product of vectors b and c, yielding a scalar value. This expression is presented as a tensor equation, showcasing its geometric and coordinate-independent nature. The video then expands this expression to illustrate the process of contraction and the significance of dummy indices, culminating in an invariant scalar value representing the volume.
📐 The Role of the Volume Element in Coordinate Systems
In this segment, the concept of the volume element, denoted as the square root of z, is introduced as a conversion factor that ensures the expression for the volume differential remains invariant across different coordinate systems. The video revisits the previously derived tensor equation, showing how the volume of the parallelepiped can be expressed as the product of the square root of z and the differential elements dz1, dz2, and dz3. This invariant expression applies universally to all coordinate systems, including Cartesian coordinates, where the volume element is 1, and the differentials are represented as dx, dy, and dz. This relationship demonstrates the universality of the volume differential in tensor calculus.
🔬 Generalizing Physical Integrals Using Invariant Volume Expression
Building on the concept of the invariant volume differential, the video discusses how to generalize the evaluation of physical integrals. The integral of a function f over the entire physical domain is expressed as a triple integral involving the function f, the volume element (square root of z), and the differentials dz1, dz2, and dz3. The limits of these integrals are chosen to match the boundaries of the physical domain in the chosen coordinate system. The video illustrates this with an example of finding the volume of a sphere, comparing the process using Cartesian coordinates with spherical polar coordinates. The spherical polar coordinate system simplifies the integration, showcasing the importance of choosing an appropriate coordinate system for simplifying complex integrations.
Mindmap
Keywords
💡Tensor Calculus
💡Physical Integral
💡Density
💡Physical Domain
💡Volume Differential
💡Cartesian Coordinate System
💡Multiple Integral
💡Spherical Polar Coordinates
💡Volume Element
💡Permutation Symbol
💡Invariant Expression
Highlights
Introduction to the concept of a physical integral and its application in calculating the mass of an object.
Explanation of the necessity of knowing the physical domain and density function for calculating mass.
Description of the physical domain represented by Greek letter omega and its importance in the integral process.
Introduction of the density function, represented by Greek letter rho, and its variability within the domain.
Process of calculating mass by multiplying volume differential with density at each point.
The concept of a physical integral as an integral of a function over the entire physical domain.
Relevance of physical integrals in various physics applications such as calculating total charge or center of mass.
Independence of physical integrals from any particular coordinate system due to their geometric nature.
Demonstration of evaluating mass using Cartesian coordinates and the challenges of choosing appropriate limits.
Introduction to the concept of a multiple integral and its role in evaluating physical integrals.
Transition from Cartesian coordinates to a more general approach using tensor calculus.
Derivation of an invariant expression for volume differentials that works for any coordinate system.
Explanation of vectors a, b, and c representing directions of basis vectors and their role in forming a parallelepiped.
Calculation of the volume of a parallelepiped using the dot product and cross product of vectors.
Inclusion of the volume element square root of z as a conversion factor for invariant expressions.
Generalization of the physical integral evaluation using the invariant expression for volume differentials.
Example of finding the volume of a sphere using spherical polar coordinates and the simplification it offers.
Strategy of avoiding commitment to a specific coordinate system and choosing the right one when necessary.
Final summary of the importance of the volume element in ensuring identical results across different coordinate systems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: