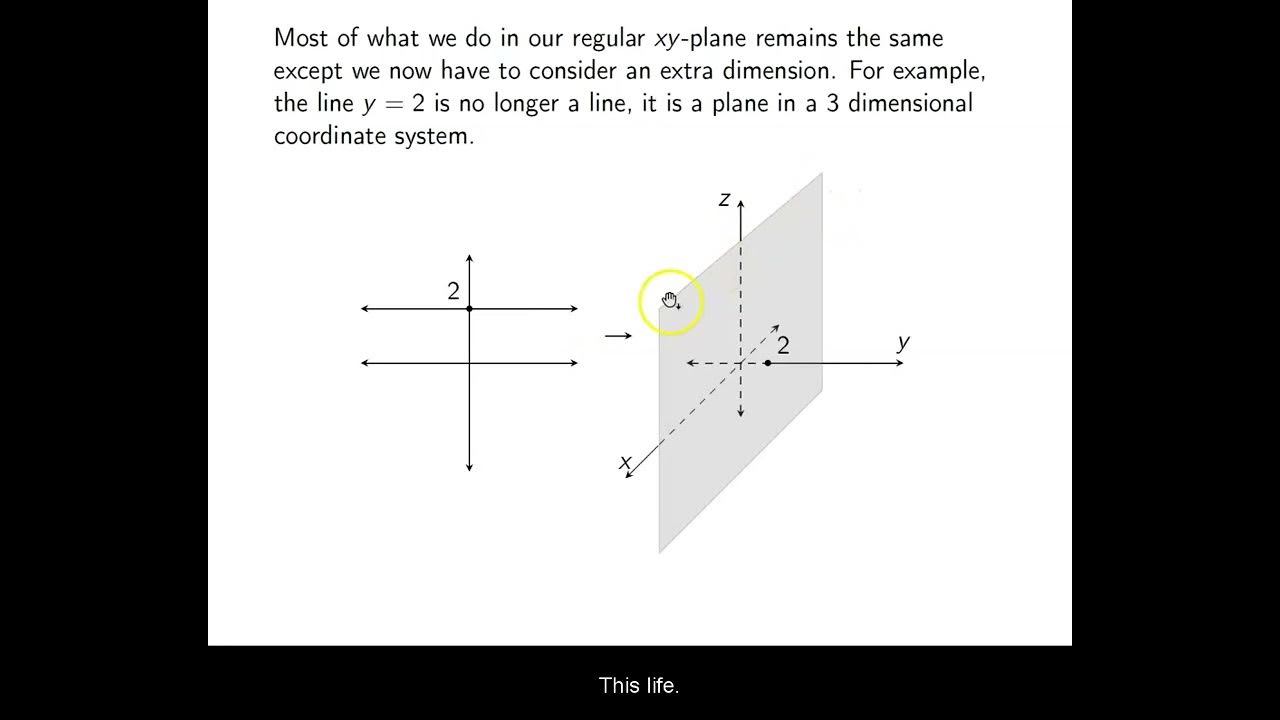
Intercepts and Traces of Surfaces (in 3D Space)

Houston Math Prep
7 Feb 202114:00
EducationalLearning
32 Likes 10 Comments

TLDRThis video by Houston Mathprep explores the concepts of intercepts and traces for surfaces in 3D space. It explains how to find intercepts by setting all but one coordinate to zero in equations of planes and spheres, revealing points where the graph intersects the axes. The video also covers traces, which are cross-sections of surfaces when they intersect with planes. Examples include finding the linear equations for traces of a plane in coordinate planes and the circular traces of a sphere, with a focus on the x, y, and z intercepts and their graphical representation.

Takeaways
  • 📍 An intercept in 3D space is a point where the graph of an equation intersects an axis, with all other coordinates being zero.
  • 📏 For a plane equation, intercepts can be found by setting the other variables to zero and solving for the remaining variable.
  • 🔍 The x-intercept of the plane 6x + 15y + 10z = 30 is at (5, 0, 0), found by setting y and z to zero and solving for x.
  • 📏 The y-intercept of the same plane is at (0, 2, 0), determined by setting x and z to zero and solving for y.
  • 📍 The z-intercept is at the origin (0, 0, 0), as setting x and y to zero leaves only 10z = 30, resulting in z = 3.
  • 🌐 For a sphere, intercepts are found similarly by setting the non-axis variables to zero and solving the resulting equation.
  • 🔄 The x-intercept of the sphere x^2 + (y - 2)^2 + z^2 = 4 is at the origin (0, 0, 0), as x^2 + 4 = 4 simplifies to x = 0.
  • 🔄 The y-intercept of the sphere has two points: (0, 4, 0) and (0, 0, 0), resulting from solving y - 2 = ±2.
  • 🔄 The z-intercept of the sphere is just the origin (0, 0, 0), as x and y set to zero leaves z^2 = 0, meaning z = 0.
  • 🔪 A trace of a surface in 3D space is a curve or cross-section formed by the intersection of the surface with a plane.
  • 📈 The trace in a coordinate plane is found by setting the variable not in the plane's name to zero and solving the resulting equation.
  • 📊 The trace of the plane 6x + 15y + 10z = 30 in the xy-plane is a line represented by 2x + 5y = 10 when z = 0.
  • 📈 The yz-trace of the same plane is a line represented by 3y + 2z = 6 when x = 0.
  • 📊 The xz-trace is also a line, represented by 3x + 5z = 15 when y = 0.
  • 🔄 The xy-trace of the sphere is a circle with center (0, 2) and radius 2 when z = 0.
  • 🔄 The yz-trace of the sphere is a circle with center (2, 0) and radius 2 when x = 0.
  • 📍 The xz-trace of the sphere is a single point at the origin (0, 0) when y = 0, as x^2 + z^2 = 0 implies both x and z are zero.
Q & A

  • What is an intercept in the context of 3D space?

    -An intercept in 3D space is a point where the graph of an equation intersects an axis, with all other coordinates being zero at that point.

  • How do you find the x-intercept of a surface in 3D space?

    -To find the x-intercept, set y and z coordinates to zero and solve the equation for x.

  • What are the coordinates of the x-intercept for the plane equation 6x + 15y + 10z = 30?

    -The x-intercept for this plane is at (5, 0, 0), found by setting y and z to zero and solving for x.

  • What is the y-intercept of the plane given by 6x + 15y + 10z = 30?

    -The y-intercept is at (0, 2, 0), found by setting x and z to zero and solving for y.

  • How do you determine the z-intercept of a surface?

    -To find the z-intercept, set x and y coordinates to zero and solve the equation for z.

  • What is the z-intercept for the sphere equation x^2 + (y - 2)^2 + z^2 = 4?

    -The z-intercept for this sphere is at the origin (0, 0, 0), as it intersects the z-axis only at this point.

  • What is a trace in 3D space and how is it different from an intercept?

    -A trace in 3D space is a curve or cross-section of a surface where it intersects a plane, as opposed to an intercept which is a point where the surface intersects an axis.

  • What is the equation of the xy-trace for the plane 6x + 15y + 10z = 30?

    -The xy-trace is a line with the equation 2x + 5y = 10, found by setting z to zero.

  • How do the traces of a sphere in the coordinate planes differ from those of a plane?

    -The traces of a sphere in the coordinate planes are circles (or a point in the case of the xz-trace), while the traces of a plane are lines.

  • What is the center and radius of the xy-trace for the sphere x^2 + (y - 2)^2 + z^2 = 4?

    -The xy-trace is a circle with a center at (0, 2) and a radius of 2.

  • What does the yz-trace of the sphere x^2 + (y - 2)^2 + z^2 = 4 represent?

    -The yz-trace is a circle in the yz-plane with a center at (2, 0) and a radius of 2.

  • Why is the xz-trace of the sphere x^2 + (y - 2)^2 + z^2 = 4 just a point?

    -The xz-trace is a point because the equation x^2 + z^2 = 0 implies that both x and z must be zero for the equation to hold true, resulting in the origin (0, 0).

Outlines
00:00
📚 Understanding Intercepts in 3D Space

This paragraph introduces the concept of intercepts for surfaces in 3D space. An intercept is a point where the graph of an equation intersects an axis, and it's characterized by all other coordinates being zero. The video script explains how to find x, y, and z intercepts for a given plane equation, using the example of the plane 6x + 15y + 10z = 30. It demonstrates the process of setting the non-intercepting variables to zero and solving for the intercepting variable, resulting in the x-intercept at (5,0,0), y-intercept at (0,2,0), and z-intercept at (0,0,3). The paragraph also briefly mentions plotting these intercepts in the first octant.

05:00
🔍 Intercepts and Traces of a Sphere

The second paragraph delves into finding intercepts for a sphere, using the equation x² + (y - 2)² + z² = 4 as an example. It explains the process of finding x, y, and z intercepts by setting the other two variables to zero and solving the resulting equation. The x-intercept is found to be the origin (0,0,0), while the y-intercept yields two points, (0,4,0) and (0,0,0), indicating the sphere intersects the y-axis at y = 4 and y = 0. The z-intercept is also the origin, showing the sphere touches the z-axis only at this point. The paragraph concludes with the observation that the intercepts provide insight into the sphere's position relative to the coordinate axes.

10:03
📐 Exploring Traces in Coordinate Planes

The final paragraph discusses traces, which are the cross-sections or curves formed when a surface intersects a plane in 3D space. It differentiates between traces in coordinate planes and those parallel to them. The script provides a method to find traces in the xy, yz, and xz planes by setting the non-trace plane variable to zero. Using the plane equation from earlier, 6x + 15y + 10z = 30, it shows how to derive the traces in each coordinate plane, resulting in linear equations representing lines in the xy and yz planes, and a single point in the xz plane. The paragraph also revisits the sphere equation to find its traces in the coordinate planes, revealing a circle with a radius of 2 in the xy and yz planes, and a single point at the origin in the xz plane, indicating the sphere's cross-sectional shapes in relation to these planes.

Mindmap
Keywords
💡Intercepts
Intercepts refer to the points where the graph of an equation intersects an axis in 3D space. In the context of the video, intercepts are essential for understanding the location of a surface in relation to the coordinate axes. For example, the x-intercept is found when y and z coordinates are zero, and the script demonstrates how to calculate it for the plane equation 6x + 15y + 10z = 30, resulting in the point (5, 0, 0).
💡3D Space
3D Space is the three-dimensional geometric space that we inhabit and perceive, consisting of length, width, and height. The video discusses concepts of intercepts and traces within this space, using it as the foundational environment for graphing equations and understanding their geometric representations.
💡Surfaces
Surfaces in the video refer to the geometric shapes that can be represented by equations in 3D space. They can be planes, spheres, or other shapes, and the video explains how to find their intercepts and traces, which are fundamental for plotting and understanding their positions and orientations in space.
💡Plane
A plane is a two-dimensional flat surface that extends infinitely in all directions. The script uses the equation 6x + 15y + 10z = 30 to represent a plane and demonstrates how to find its x, y, and z intercepts, which are essential for plotting the plane in 3D space.
💡Sphere
A sphere is a perfectly round three-dimensional object in space, with all points on its surface equidistant from its center. The video script provides the equation x^2 + (y - 2)^2 + z^2 = 4 to represent a sphere and explains how to find its intercepts, showing that the sphere intersects the coordinate axes at specific points.
💡Traces
Traces are the curves or cross-sections that result from the intersection of a surface with a plane in 3D space. The video explains that traces can be found in coordinate planes by setting the variable not mentioned in the trace's name to zero, and it uses the examples of a plane and a sphere to illustrate how to find traces in the xy, yz, and xz planes.
💡Coordinate Planes
Coordinate planes are the two-dimensional planes defined by the intersections of the coordinate axes in 3D space. The script mentions the xy, yz, and xz planes and explains how to find traces of surfaces within these planes by setting the appropriate variable to zero.
💡Equation
An equation in the context of the video represents a relationship between variables that can describe a geometric shape in 3D space. Equations are used to calculate intercepts and traces, as demonstrated with the plane and sphere equations in the script.
💡Graph
A graph in the video refers to the visual representation of the set of points that satisfy an equation in 3D space. The script discusses how to plot the graph of a plane using its intercepts and how the traces of surfaces appear when graphed in the coordinate planes.
💡Cross-Section
A cross-section in the video is the shape that is revealed when a surface is cut by a plane. The script explains that traces are a type of cross-section, showing how surfaces like a plane or a sphere appear when intersected by the coordinate planes.
💡Slope
Slope is a measure of the steepness of a line, and in the video, it is mentioned in the context of finding the trace of a plane in the coordinate planes. The script shows how to simplify the equations of traces to find their slope and intercept, which helps in plotting them in the coordinate planes.
💡Radius
The radius of a circle is the distance from its center to any point on its circumference. The video script explains that the traces of a sphere in the xy and yz planes are circles with a radius of 2, which is determined by the equation of the sphere.
Highlights

Intercepts in 3D space are points where the graph of an equation intersects an axis, with all other coordinates being zero at that intercept.

For an x-intercept, both y and z coordinates are zero; for a y-intercept, x and z are zero; and for a z-intercept, x and y are zero.

Finding intercepts involves setting the non-intercepting variables to zero and solving the resulting equation.

The plane equation 6x + 15y + 10z = 30 has intercepts calculated by setting y and z to zero for the x-intercept, and similarly for y and z intercepts.

The x-intercept of the plane is at (5, 0, 0), found by solving 6x = 30.

The y-intercept is at (0, 2, 0), determined by solving 15y = 30.

The z-intercept is at (0, 0, 3), obtained by solving 10z = 30.

Intercepts can be used to plot a section of a plane in the first octant.

A sphere's intercepts are calculated by setting two variables to zero and solving for the third.

The sphere equation x^2 + (y - 2)^2 + z^2 = 4 has an x-intercept at the origin (0, 0, 0).

The y-intercept of the sphere includes points (0, 4, 0) and (0, 0, 0), found by solving (y - 2)^2 = 4.

The z-intercept of the sphere is also at the origin, as z^2 = 0 when x and y are zero.

Traces in 3D space are curves or cross-sections of a surface where it intersects a plane.

Traces can be found in coordinate planes by setting the variable not mentioned in the trace's name to zero.

The xy-trace of the plane 6x + 15y + 10z = 30 is a line 2x + 5y = 10 when z = 0.

The yz-trace of the same plane is a line 3y + 2z = 6 when x = 0.

The xz-trace is a line 3x + 5z = 15 when y = 0.

The xy-trace of the sphere is a circle with center (0, 2) and radius 2 when z = 0.

The yz-trace of the sphere is a circle with center (2, 0) and radius 2 when x = 0.

The xz-trace of the sphere is a point at the origin (0, 0) when y = 0, as it represents a circle with radius 0.

Transcripts

Browse More Related Video

Calculus 3: Three-Dimensional Coordinate Systems (Video #1) | Math with Professor V

Normal Vectors and Equations of Planes (Calculus 3)

Quadric Surfaces (Calculus 3)

Ch. 9.3 Three Dimensional Coordinate Geometry

Three-Dimensional Coordinates and the Right-Hand Rule

Cylinders (Calculus 3)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
3D GeometryInterceptsTracesSurfacesEducationalMathematicsVideo TutorialPlane EquationSphere GeometryCoordinate PlanesCross Sections