18.2 Entropy | General Chemistry

Chad's Prep

3 Mar 202225:24

EducationalLearning

32 Likes 10 Comments

TLDRIn this lesson on entropy, Chad from Chad's Prep demystifies the concept by explaining its correlation with randomness and disorder. He discusses the statistical mechanics definition of entropy, focusing on microstates, and touches on the classical thermodynamics perspective. Chad also explores factors affecting entropy, such as phase, temperature, volume, and the number of particles. He provides practical examples to illustrate how to predict changes in entropy. This video is part of Chad's new general chemistry playlist aimed at high school, college, and test prep students. For more in-depth learning, additional courses are available on his website.

Takeaways

📚 The lesson is about entropy, taught by Chad from Chad's Prep, focusing on simplifying science learning.
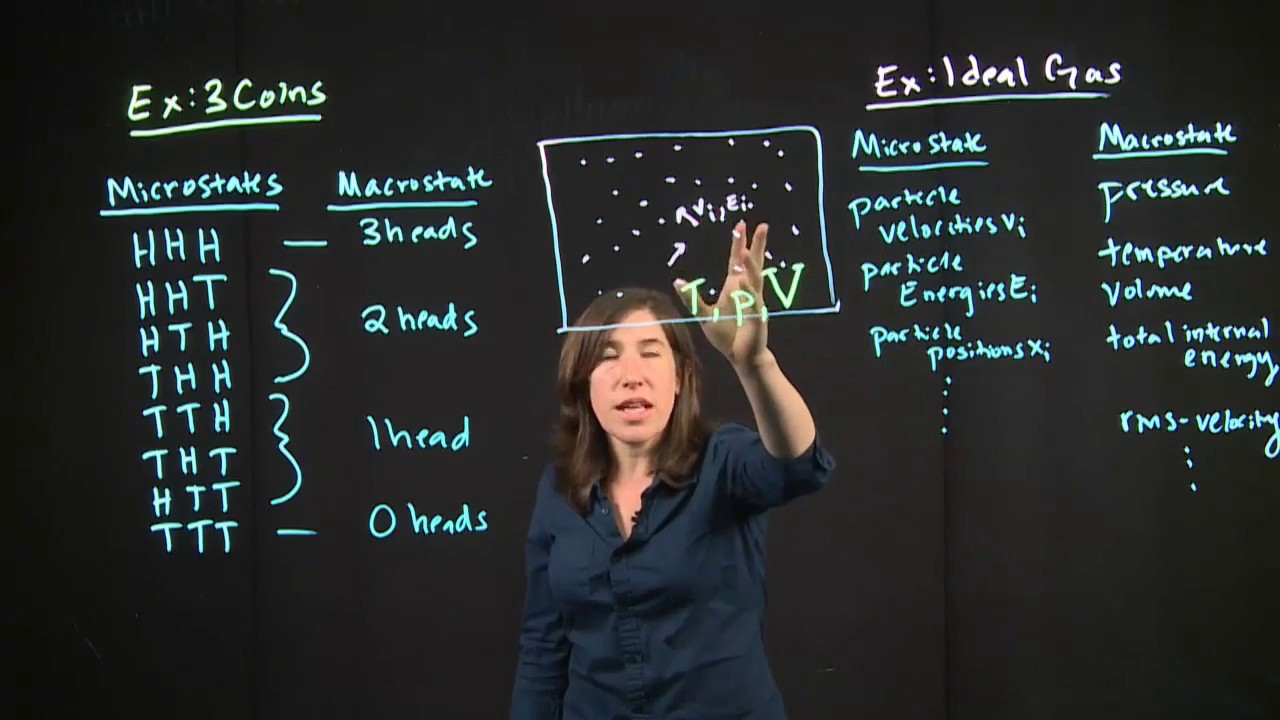
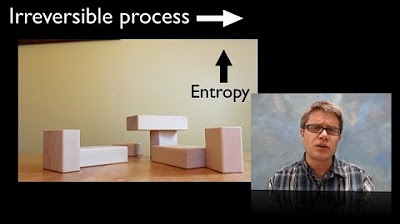
🔬 Entropy is related to but not equivalent to randomness or disorder; it's a measure of the number of microstates in a system.
📈 Entropy is represented by the letter 'S' and is calculated using the formula involving the Boltzmann constant and the natural log of the number of microstates (ω).
🧩 At absolute zero, a perfect crystal has zero entropy because it has only one microstate, fulfilling the third law of thermodynamics.
🔑 The Boltzmann constant (k or KB) is a fundamental constant in statistical mechanics, relating to the energy per degree of freedom of a particle in a gas.
♨️ Entropy increases with temperature due to increased molecular motion and the resulting increase in possible microstates.
💧 When substances dissolve in water, they generally exhibit an increase in entropy due to the greater disorder and randomness in the aqueous phase.
🌡️ Phase changes, particularly from solid to liquid to gas, are associated with increases in entropy, reflecting greater disorder.
🌌 Entropy is also affected by the complexity of molecules; more complex molecules have more potential microstates and thus higher entropy.
🌟 The number of moles of gas is a significant factor in predicting entropy changes (ΔS) in chemical reactions; an increase in moles of gas usually indicates a positive ΔS.
🔄 Mixing substances typically results in an increase in entropy due to the increased disorder and number of microstates that can exist in the mixture.

Q & A

What is the main topic of Chad's lesson?
-The main topic of Chad's lesson is entropy, which is a complex concept in the field of chemistry.
What is Chad's goal with his lessons?
-Chad's goal with his lessons is to take the stress out of learning science and to provide high school, college, MCAT, DAT, and OAT prep.
What is the statistical mechanics definition of entropy?
-From a statistical mechanics perspective, entropy (abbreviated as S) is related to the number of microstates (denoted as W or omega), which are the unique states that a system can exist in.
What is the Boltzmann constant and its value?
-The Boltzmann constant (denoted as k or KB) is a fundamental constant in physics that is approximately 1.38 x 10^-23 joules per Kelvin.
How does the number of microstates relate to entropy?
-The more microstates a system has, the more entropy it has. As the number of microstates increases, so does the entropy.
What is the significance of the third law of thermodynamics in the context of entropy?
-The third law of thermodynamics states that as the temperature of a perfect crystal approaches absolute zero Kelvin, its entropy approaches zero because there is only one microstate in which the substance can exist.
How does the phase of a substance affect its entropy?
-The phase of a substance greatly affects its entropy, with solids having the least entropy, liquids having more, and gases having the most due to their increased disorder and volume.
What is the relationship between temperature and entropy?
-As temperature increases, so does entropy, because higher temperatures lead to more molecular motion, which in turn leads to more microstates and greater disorder.
How does the volume of a system relate to its entropy?
-Greater volume leads to greater entropy because it provides more potential locations for atoms and molecules, increasing the number of microstates and thus the entropy.
What is the significance of the number of particles in a system in terms of entropy?
-The more particles in a system, the more microstates there can be, leading to greater entropy. This is because each particle can occupy different positions, contributing to the overall disorder and randomness.
How can the complexity of molecules affect entropy?
-The complexity of molecules, such as the number of atoms and the variety of atoms present, can affect entropy. More complex molecules have more possible orientations and configurations, leading to a greater number of microstates and higher entropy.
What is the primary factor to consider when predicting the sign of ΔS (entropy change) in a reaction?
-The primary factor to consider when predicting the sign of ΔS is the number of moles of gas involved in the reaction. An increase in the number of moles of gas generally indicates a positive ΔS, while a decrease indicates a negative ΔS.

Outlines

00:00

🔬 Introduction to Entropy and Chad's Prep

Chad introduces the topic of entropy in this lesson, emphasizing its complexity and its correlation with randomness and disorder, though not being equivalent. He outlines the course offerings for high school, college, and standardized test preparation, and invites viewers to subscribe for updates. Chad then sets the stage for the statistical mechanics perspective on entropy, relating it to the number of microstates a system can have, symbolized by 'W' or 'omega', and explains how entropy is calculated using the Boltzmann constant.

05:04

📚 Entropy and Microstates in Statistical Mechanics

The lesson delves into the statistical mechanics definition of entropy, highlighting its relationship with the number of microstates. Chad explains that entropy increases with the number of microstates, reaching zero when there is only one possible state. He also clarifies the difference between the Boltzmann constant and the universal gas constant, and discusses how cooling a substance to absolute zero reduces it to a single microstate, aligning with the third law of thermodynamics.

10:04

🌡️ Factors Influencing Entropy: Phase, Temperature, and Volume

Chad explores the factors affecting entropy, starting with the phase of matter, where gases have more entropy than liquids, which in turn have more than solids. He then connects temperature and entropy, noting that higher temperatures lead to increased molecular motion and thus more entropy. Volume is the next factor, with greater volumes providing more space for molecules to exist in, leading to a higher number of microstates and increased entropy.

15:04

🧩 Complexity and Particles' Contribution to Entropy

This paragraph examines how the complexity of molecules and the number of particles within a system contribute to entropy. Chad uses the example of helium, hydrogen, and methanol to illustrate how more complex molecules with a greater variety of atoms have more microstates and therefore more entropy. He also touches on the concept of degrees of freedom related to molecular rotation.

20:05

🌟 Predicting Entropy Changes: Delta S Sign

Chad teaches how to predict the sign of entropy changes (Delta S) by focusing on the number of moles of gas, phase changes, and the complexity of molecules. He explains that an increase in the moles of gas typically results in a positive Delta S, while phase changes from gas to liquid to solid correspond to negative Delta S values. Dissolving a substance in water is also discussed as a process that generally increases entropy.

25:06

📈 Entropy in Chemical Reactions and Processes

The final paragraph provides examples of chemical reactions and processes to demonstrate the application of predicting entropy changes. Chad clarifies that the presence of gases, phase changes, and mixing of substances are critical in determining whether Delta S is positive or negative. He concludes by emphasizing the complexity of the subject and invites students to explore further in his physical chemistry course.

📘 Conclusion and Resource Recommendation

Chad concludes the lesson by encouraging students to like and comment if they found the content helpful. He promotes his general chemistry master course for further study in thermodynamics and other topics, offering a free trial and providing a link in the description for interested students.

Mindmap

Keywords

💡Entropy

Entropy is a fundamental concept in thermodynamics, often associated with the degree of disorder or randomness in a system. In the video, entropy is defined from both statistical mechanics and classical thermodynamics perspectives. It is crucial for understanding how to predict whether a process will increase or decrease in disorder, as exemplified by the discussion on microstates and the Boltzmann constant. The script mentions that entropy is not equivalent to randomness but correlates with it, making it a central theme for discussing system changes.

💡Microstates

Microstates refer to the unique arrangements or configurations that a system can occupy. In the context of the video, the number of microstates (denoted by omega) is directly related to the entropy of a system. The greater the number of microstates, the higher the entropy, indicating a system with more disorder. The script explains that systems with only one microstate have zero entropy, aligning with the third law of thermodynamics.

💡Boltzmann Constant

The Boltzmann constant (k or KB) is a physical constant that relates the energy at the molecular level to the temperature of a system. In the script, it is mentioned as 1.38 x 10^-23 joules per Kelvin. It plays a pivotal role in the statistical definition of entropy, where entropy is proportional to the natural logarithm of the number of microstates multiplied by the Boltzmann constant.

💡Third Law of Thermodynamics

The third law of thermodynamics states that the entropy of a perfect crystal approaches zero as the temperature approaches absolute zero. In the video, this is used to illustrate that at absolute zero, a system has only one microstate, hence zero entropy. It is a fundamental principle that helps understand the minimum entropy a system can possess.

💡Phase Changes

Phase changes, such as melting, boiling, and sublimation, involve transitions between solid, liquid, and gas states. The video script explains that these changes typically result in an increase in entropy, moving from a more ordered state to a less ordered one. Conversely, freezing, condensation, and deposition are associated with a decrease in entropy, as they involve moving to a more ordered state.

💡Degrees of Freedom

Degrees of freedom refer to the number of independent ways a molecule can move or rotate. In the script, it is mentioned in the context of molecular complexity and its impact on entropy. A molecule with more atoms or more complex structures has more degrees of freedom, leading to a greater number of microstates and higher entropy.

💡Spontaneity

Spontaneity in thermodynamics refers to the natural tendency of a process to occur without external interference. The video script touches on the relationship between entropy change (ΔS) and spontaneity, indicating that processes leading to an increase in entropy are generally spontaneous, especially when discussing mixing and phase changes.

💡Moles of Gas

The number of moles of gas is a significant factor in determining the entropy change of a reaction. The script emphasizes that an increase in the moles of gas from reactants to products results in a positive ΔS, while a decrease results in a negative ΔS. Gases have more entropy than solids or liquids due to their greater volume and molecular motion.

💡Temperature

Temperature is a measure of the average kinetic energy of the particles in a system. The video script explains that higher temperatures lead to more molecular motion, resulting in more microstates and thus higher entropy. Conversely, as temperature decreases, molecular motion slows, reducing the number of microstates and entropy.

💡Volume

Volume is another key factor affecting entropy. The script illustrates that a larger volume provides more space for molecules to exist in, leading to a greater number of microstates and higher entropy, especially for gases. This concept is used to explain why gases have more entropy than liquids or solids.

💡Complexity

Complexity in the context of the video refers to the structural complexity of molecules and how it relates to entropy. More complex molecules, with a variety of atoms and potential orientations, have more microstates and thus higher entropy. The script uses the example of methanol (CH3OH) to illustrate a molecule with higher complexity and entropy compared to simpler molecules like helium or hydrogen.

Highlights

Entropy is correlated with randomness or disorder, but it's not the same thing.

Entropy (S) is related to the number of microstates (W or omega) a system can exist in.

More microstates lead to more entropy.

If a system has exactly one microstate, it has zero entropy.

The Boltzmann constant (KB) is 1.38 x 10^-23 joules per Kelvin.

Entropy is zero at absolute zero Kelvin for a perfect crystal due to having only one microstate.

Mixtures have more entropy than pure substances because they have more microstates.

Solids have the least amount of entropy, liquids have more, and gases have the most.

Higher temperature leads to more entropy due to increased molecular motion.

Greater volume leads to greater entropy, especially for gases.

More particles in a system lead to more entropy.

Complex molecules have more entropy than simpler ones due to more possible microstates.

Phase changes from solid to liquid, liquid to gas, or solid to gas increase entropy.

Dissolving a solid into a liquid typically increases entropy.

Mixing substances usually increases entropy due to more microstates.

Transcripts

Browse More Related Video

18.3 Gibbs Free Energy and the Relationship between Delta G, Delta H, & Delta S | General Chemistry

Reconciling thermodynamic and state definitions of entropy | Physics | Khan Academy

6.1 Reaction Enthalpy and Bond Dissociation Energy | Organic Chemistry

Entropy intuition | Thermodynamics | Physics | Khan Academy

Micro vs Macro States

Entropy

Related Tags

Entropy Science Education Thermodynamics Chad's Prep MCAT Prep DAT Prep OAT Prep General Chemistry Statistical Mechanics Phase Changes Disorder