Euler's real identity NOT e to the i pi = -1

Mathologer

11 Aug 201717:16

EducationalLearning

32 Likes 10 Comments

TLDRThis Mathologer video explores the true Euler identity, which surprisingly equates pi squared over six to the sum of the reciprocals of the squares. It delves into Euler's ingenious proof involving the sine function's Maclaurin series, and how he derived this identity from the infinite product of sine's zeros. The video also touches on the historical oversight of Roger Cotes, the importance of the Riemann zeta function, and the connection between Euler's sum and the Leibniz formula, offering a fascinating journey through mathematical history and discovery.

Takeaways

🧩 The script clarifies that Euler's identity, often mistakenly attributed to Euler, was actually first discussed by Roger Cotes in 1714.
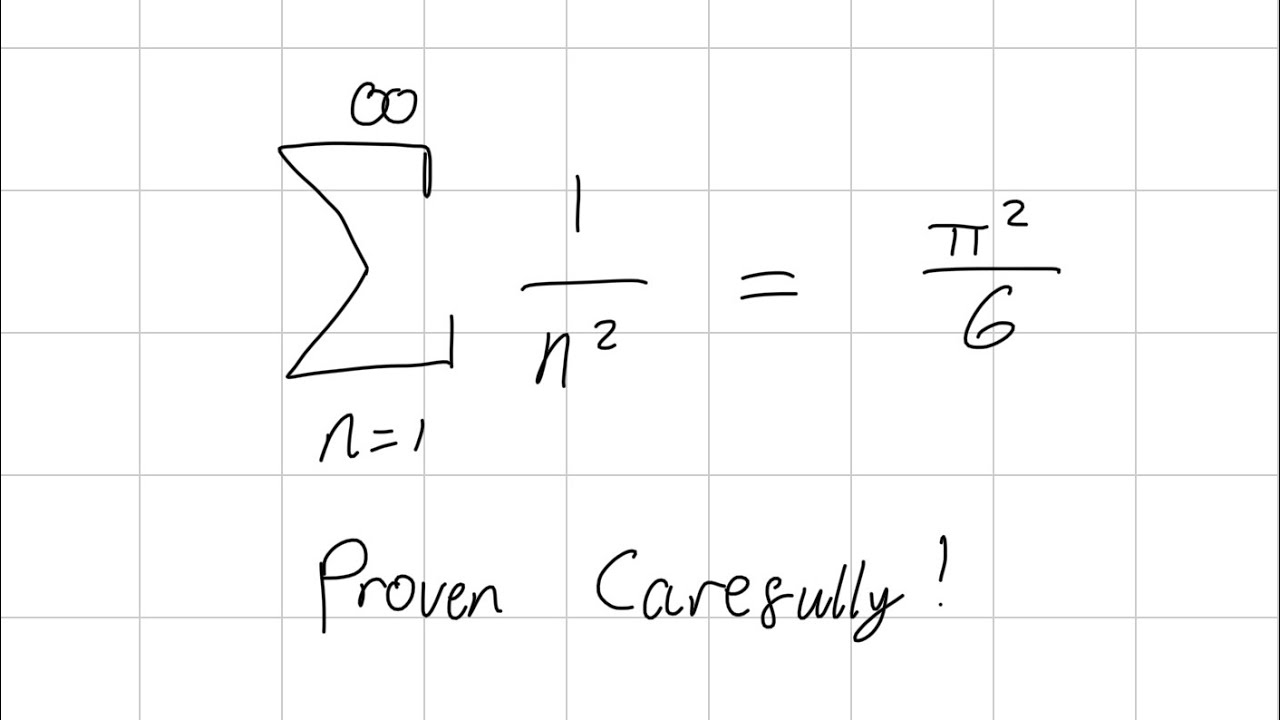
🌟 The 'real' Euler identity discussed in the video is \( \frac{\pi^2}{6} = \sum_{n=1}^{\infty} \frac{1}{n^2} \), which Euler proved in 1734, solving a previously unanswered question about the sum of reciprocals of squares.
🔍 Euler's identity is significant because it involves \( \pi \) without any direct reference to circles, and it is related to the Riemann zeta function, central to the Riemann hypothesis, an unsolved problem in mathematics.
📈 Euler's work on the zeta function at even integers all involve \( \pi \), but the values at odd integers remain unknown.
🤔 Euler was one of the pioneers in exploring the sum of the series 1+2+3+..., demonstrating that these 'exploding sums' have more depth than initially apparent.
📚 The video provides a warm-up by rewriting Euler's sum and comparing it to a related infinite sum, showing that infinite sums can indeed converge to finite values.
📉 The script uses a 'telescoping sum' argument to demonstrate that a related infinite sum converges to 2, providing insight into the convergence of Euler's sum.
📈 Euler's proof of his identity starts with the Maclaurin series for the sine function, which is derived from the circle and involves \( \pi \) in various ways.
📚 The method of deriving the Maclaurin series for sine is explained, involving taking derivatives and evaluating them at zero to find coefficients.
🔍 Euler's ingenious proof involves constructing an infinite polynomial from the zeros of sine and comparing it to the sine function's Maclaurin series to derive his identity.
📉 The script describes how Euler used numerical evidence to support his argument, which he had to produce by hand due to the lack of computational tools at the time.
📚 The video concludes by mentioning that Euler's proof was not immediately rigorous and took a few years to fully formalize.
🌐 The script also touches on the Wallis product, an infinite product for \( \frac{\pi}{2} \), and the Leibniz formula, which can be derived similarly to Euler's sum.
🌐 It is noted that the Leibniz formula and the Maclaurin series were known to Indian mathematicians centuries before Leibniz and Maclaurin, possibly due to Madhava of Sangamagrama.

Q & A

Who originally wrote about the equation e^(iπ) = -1 before Euler?
-The mathematician Roger Cotes wrote about the equation e^(iπ) = -1 in 1714.
What is the real Euler identity that made Euler a mathematical celebrity?
-The real Euler identity that made him famous is π²/6 = Σ (1/n²) for n=1 to infinity.
Why is the identity π²/6 = Σ (1/n²) surprising?
-It was surprising because it shows that the infinite sum of the reciprocals of the squares of natural numbers adds up to a finite value involving π, despite no obvious connection to circles.
What mathematical function is at the heart of the Riemann hypothesis?
-The Riemann zeta function is at the heart of the Riemann hypothesis.
How did Euler find the precise value of the Riemann zeta function at 2?
-Euler found the precise value of the Riemann zeta function at 2 by proving that the infinite sum of the reciprocals of the squares of natural numbers equals π²/6.
What method did Euler use to prove his identity involving π?
-Euler used the Maclaurin series expansion of the sine function and compared it with an infinite product expansion to prove his identity involving π.
What is the significance of the infinite sum 1/2 + 1/4 + 1/8 + ...?
-The infinite sum 1/2 + 1/4 + 1/8 + ... telescopes to 1, demonstrating that some infinite sums can add to nice values, giving hope for similar results with other sums.
How did Euler construct the infinite polynomial for the sine function?
-Euler constructed the infinite polynomial for the sine function using its zeros and expanded the infinite product to match the Maclaurin series.
What is the Wallis product, and how is it derived from Euler's work?
-The Wallis product, derived by setting x = π/2 in Euler's infinite product for sine, is an infinite product of the form (2/1) * (2/3) * (4/3) * (4/5) * ..., involving squares of even and odd numbers.
What did Euler point out about the Leibniz formula for π?
-Euler pointed out that the Leibniz formula for π can be derived similarly to his sum by writing the function 1 - sin(x) as a product using its zeros and comparing coefficients.

Outlines

00:00

😔 Misattribution of Euler's Identity

This paragraph discusses the common misconception that Euler's identity is 'e^(iπ) + 1 = 0', when in fact, it was first mentioned by Roger Cotes in 1714, before Euler's major contributions. The speaker expresses disappointment that Euler is often associated with this identity rather than his many original discoveries. It also highlights the obscurity of Roger Cotes, who is rarely credited for his work, and introduces the 'real' Euler identity, which is the focus of the video: the infinite sum of the reciprocals of the squares equating to π²/6. This identity was groundbreaking at the time and is integral to the Riemann hypothesis, one of mathematics' most significant unsolved problems.

05:01

🔍 Euler's Approach to Infinite Sums

The speaker warms up by examining infinite sums, specifically focusing on a closely related sum to Euler's identity. By rewriting Euler's sum and comparing it term by term with another infinite sum, the video demonstrates that the latter sum is greater, providing a finite value. The 'telescoping' technique is introduced to evaluate the sum, showing how it collapses to a finite value, hinting at the possibility that Euler's sum might also yield a finite, 'nice' value. The paragraph concludes with the observation that the value of π²/6 is less than 2, suggesting that Euler's sum is finite.

10:05

📚 Euler's Proof Using Maclaurin Series

Euler's method of proving his identity is explored, starting with the Maclaurin series for the sine function, an infinite polynomial representation of sine. The process of deriving this series by setting x to zero and finding coefficients through derivatives is explained. The video then delves into Euler's innovative approach of constructing an infinite polynomial from the zeros of sine, resulting in a close approximation to the sine function. The paragraph concludes with Euler equating two infinite expressions, sine x, and expanding the infinite product to recover the infinite sum, leading to his identity.

15:08

🎓 Euler's Identity and Its Implications

The final paragraph wraps up the discussion by highlighting Euler's delayed rigorous proof of his identity and presents two additional fascinating facts. The first is the Wallis product, an infinite product representation of π/2 derived from Euler's sine expression. The second is the connection between Euler's sum and the Leibniz formula, suggesting a similar derivation method. The speaker also laments the lack of recognition for Indian mathematicians, particularly Madhava of Sangamagrama, who predated Leibniz and Maclaurin by centuries. The video concludes with an invitation for feedback and a promise of future content.

Mindmap

Keywords

💡Euler's identity

Euler's identity, often expressed as e^(iπ) + 1 = 0, is a fundamental equation in complex analysis that involves the exponential function, the imaginary unit, and pi. In the video, it's mentioned that this identity is commonly attributed to Euler, though Roger Cotes discussed it earlier. The video focuses on a different, lesser-known identity by Euler involving pi squared over six.

💡Roger Cotes

Roger Cotes was an English mathematician who wrote about the identity e^(iπ) = -1 in 1714, predating Euler's well-known work on the topic. The video highlights that despite Cotes' earlier contribution, Euler is more commonly associated with this identity, overshadowing Cotes' work.

💡Pi squared over six

The identity π^2/6 is equal to the sum of the reciprocals of the squares of the natural numbers (1 + 1/4 + 1/9 + ...). This surprising result, which Euler discovered, was a major breakthrough in the 18th century and established Euler's reputation in the mathematical community. It shows an unexpected connection between a geometric constant (pi) and an infinite series.

💡Riemann zeta function

The Riemann zeta function, denoted ζ(s), is a complex function that is significant in number theory and mathematical analysis. The video explains that Euler determined the values of this function at even integers, starting with ζ(2) = π^2/6. This function is central to the Riemann hypothesis, one of the most famous unsolved problems in mathematics.

💡Maclaurin series

The Maclaurin series is a type of Taylor series expansion of a function about zero. In the video, the series for sine is used to derive Euler's identity. The series expresses sine as an infinite polynomial, which is fundamental in understanding Euler's proof.

💡Infinite sum

An infinite sum (or series) is the sum of an infinite sequence of terms. The video discusses the sum of the reciprocals of the squares of natural numbers, which Euler proved equals π^2/6. This concept is crucial for understanding the surprising and elegant results in mathematical analysis.

💡Telescoping series

A telescoping series is a series where most terms cancel out when the series is expanded. In the video, a telescoping argument is used to simplify and sum an infinite series, illustrating the concept with partial sums that collapse to a finite value.

💡Sine function

The sine function, sin(x), is a fundamental trigonometric function. Euler used its Maclaurin series to derive his identity involving π^2/6. The video demonstrates how the sine function can be expressed as an infinite polynomial and an infinite product, both of which are used in Euler's proof.

💡Zeros of sine

The zeros of the sine function are the values of x where sin(x) = 0, occurring at integer multiples of π. In the video, Euler uses these zeros to construct an infinite polynomial that represents the sine function, which is pivotal in his proof of the identity involving π^2/6.

💡Wallis product

The Wallis product is an infinite product for π/2 that involves the ratio of even to odd numbers. The video mentions that setting x = π/2 in the sine function's infinite product representation leads to this beautiful product, showcasing another fascinating connection between infinite products and pi.

💡Leibniz formula

The Leibniz formula for π is an alternating series that converges to π, given by π = 4(1 - 1/3 + 1/5 - 1/7 + ...). The video notes that this formula, like Euler's identity, can be derived using the zeros of sine and its series representation, illustrating the deep interconnections in mathematical analysis.

💡Maclaurin series coefficients

Coefficients in the Maclaurin series are the constants in front of each term in the series expansion of a function. The video shows how to derive these coefficients for the sine function, which are essential for forming the infinite polynomial used in Euler's proof.

Highlights

Euler's identity is often mistakenly attributed to Euler, but it was first written about by Roger Cotes in 1714.

The real Euler identity is the infinite sum of the reciprocals of the squares, which equals pi squared over six.

Euler's discovery was significant as it provided a surprising answer to the problem of the infinite sum.

The identity is related to the Riemann zeta function, central to the Riemann hypothesis, an unsolved problem in mathematics.

Euler found the value of the Riemann zeta function for all even numbers, which all involve the number pi.

Euler was also interested in assigning values to exploding sums, such as 1+2+3+..., and demonstrated their deeper significance.

Euler's proof involves the Maclaurin series of the sine function, a method of expressing sine as an infinite polynomial.

The sine function's Maclaurin series is derived from its derivatives at zero, providing a formula for all famous functions.

Euler used a method of constructing infinite polynomials based on the zeros of sine to derive his identity.

By comparing coefficients of the infinite sum and the expanded product, Euler derived his identity and other related identities.

Euler's method involves expanding the infinite product term-by-term to eventually recover the infinite sum.

The x cubed term of the expanded infinite product must equal the x cubed term of the infinite sum, leading to Euler's identity.

Euler's sum can be derived in a similar way to the Leibniz formula by writing 1 - sine x as a product using its zeros.

The Wallis product, an infinite product for pi/2, can be derived from Euler's sine representation by setting x to pi/2.

The video emphasizes the importance of recognizing the contributions of lesser-known mathematicians like Roger Cotes and Madhava.

Euler's work on infinite sums and products laid the groundwork for deeper understanding in mathematical analysis.

The video provides a simplified explanation of Euler's proof, highlighting the ingenious use of infinite series and products.

Euler's identity is not only aesthetically pleasing but also practically important in the field of mathematics.

Transcripts

Browse More Related Video

Proof Of The Basel Problem

Euler's infinite pi formula generator

Ramanujan's easiest hard infinity monster (Mathologer Masterclass)

Pi is IRRATIONAL: animation of a gorgeous proof

Euler's formula & Euler's identity | Series | AP Calculus BC | Khan Academy

700 years of secrets of the Sum of Sums (paradoxical harmonic series)