Euler's infinite pi formula generator
TLDRIn this Mathologer video, we embark on a mathematical journey exploring Leonhard Euler's ingenious leap of faith, which led to the derivation of the sine function as an infinite product. The video demonstrates how this concept can be manipulated to unveil various infinite expressions for pi, including the Leibniz-Madhava formula, Wallis' infinite product, and Brouncker's infinite fraction. Euler's Basel problem solution and its higher power counterparts are also highlighted, showcasing Euler's extraordinary contributions to mathematics.
Takeaways
- 📚 The video revisits the mathematical genius of Leonhard Euler and his 'crazy leap of faith' that led to significant formulas for pi.
- 🔑 Euler's work resulted in a 'magic key' that unlocked several famous formulas for pi, including the Leibniz-Madhava formula, Wallis' infinite product formula, and Brouncker's infinite fraction formula.
- 🌟 Euler's formula for solving the Basel problem catapulted him to mathematical stardom at the age of 28.
- 🎓 The video credits Paul Levrie's 2012 article in the Mathematical Intelligencer for inspiring the content, which provides quick derivations of these mathematical results.
- 🤔 The script poses a question about the uniqueness of a cubic polynomial given its zeros, illustrating that knowing the zeros of a polynomial can define it up to a scaling factor.
- 🛫 Euler's 'mad flight of mathematical fantasy' involved treating functions like sine as infinite polynomials and attempting to express them as products based on their zeros.
- 🧙♂️ Euler's product formula for sine, derived through a non-rigorous 'Nike method' of 'just do it and see what happens', is presented as an example of how even wild ideas can lead to profound insights.
- 📈 The video demonstrates how to derive various infinite expressions for pi from Euler's product formula by using logarithmic differentiation and other algebraic manipulations.
- ✨ The Leibniz-Madhava formula for pi is obtained by evaluating Euler's product formula at pi/4 and applying logarithmic differentiation.
- 🔄 The script shows an ingenious method to transform the Leibniz-Madhava formula into an infinite fraction, akin to Brouncker's formula, through a series of algebraic 'combo moves'.
- 🔍 Euler's Basel formula is derived by expanding and simplifying Euler's product formula, differentiating multiple times, and evaluating at specific points to isolate powers of pi.
- 🔗 The video concludes by highlighting Euler's general formula for pi to the power of 2n, which is connected to the Riemann zeta-function and Bernoulli numbers, inviting viewers to explore these deeper mathematical connections.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is the exploration of mathematical formulas for pi, particularly focusing on Euler's infinite product formula for sine and its derivations.
Who is Leonhard Euler and why is he significant in this context?
-Leonhard Euler was an 18th-century mathematician known for his extensive work in various fields of mathematics. In this context, he is significant for his 'crazy leap of faith' that resulted in an infinite product formula for sine, which is foundational for deriving various formulas for pi.
What is the significance of Euler's product formula for sine in deriving formulas for pi?
-Euler's product formula for sine is significant because it serves as a basis for deriving various infinite expressions for pi, including the Leibniz-Madhava formula, Wallis's infinite product formula, and Euler's own formula for the Basel problem.
What is the Basel problem that Euler solved?
-The Basel problem is a mathematical problem that involves finding the exact value of the sum of the reciprocals of the squares of the natural numbers, which Euler solved using his infinite product formula for sine.
What is the Leibniz-Madhava formula for pi mentioned in the video?
-The Leibniz-Madhava formula for pi is an infinite series representation of pi, which can be derived from Euler's product formula for sine by applying logarithms, differentiating, and evaluating at pi over four.
How does the video describe the process of deriving an infinite sum from a product?
-The video describes the process of deriving an infinite sum from a product by using logarithms to convert the product into a sum and then differentiating to simplify the expression, ultimately leading to the Leibniz-Madhava formula for pi.
What is the connection between Euler's product formula for sine and the infinite fraction formula for pi?
-The connection between Euler's product formula for sine and the infinite fraction formula for pi is established through a series of mathematical manipulations, including taking logarithms, differentiating, and evaluating at specific values, which eventually leads to the infinite fraction representation of pi.
What is the Weierstrass factorisation theorem mentioned in the video?
-The Weierstrass factorisation theorem is a mathematical theorem that states that every entire function can be represented as a product involving its zeros, which is related to Euler's infinite product formula for sine.
How does the video illustrate the process of deriving Euler's Basel formula?
-The video illustrates the process of deriving Euler's Basel formula by expanding the infinite product for sine, collecting different powers of x, and then differentiating and setting x to zero to isolate the terms involving pi squared.
What are the challenges presented by the video for the viewers to try on their own?
-The video presents challenges for viewers to derive the pi to the power of six formula and to identify and understand the details that need to be addressed to turn the derivations into rigorous proofs.
Outlines
📚 Euler's Mathematical Leap of Faith
This paragraph introduces the video's theme, focusing on the 18th-century mathematician Leonhard Euler's innovative approach to mathematics. Euler's 'crazy leap of faith' led to the discovery of key formulas for pi, including the Leibniz-Madhava formula, Wallis' infinite product formula, and Brouncker's infinite fraction formula. The video promises to guide viewers through Euler's thought process and reveal animated algebra that brings these formulas to life. The inspiration for this exploration comes from Paul Levrie's 2012 article in the Mathematical Intelligencer, which provided quick derivations of these results. The paragraph also poses a question about the uniqueness of polynomials based on their zeros, setting the stage for Euler's infinite polynomial concept.
🔍 Euler's Infinite Product for Sine
The paragraph delves into Euler's imaginative method of treating functions as infinite polynomials, specifically using the sine function as an example. Euler hypothesized that since sine can be represented as an infinite polynomial (its Maclaurin series), it could also be expressed as an infinite product based on its zeros. The paragraph describes Euler's unconventional approach to deriving this product formula, which involved ignoring the Maclaurin series and instead constructing an infinite product from the zeros of sine. Despite the seemingly illogical steps, the final formula is not only meaningful but also true, demonstrating Euler's extraordinary intuition and the power of mathematical exploration beyond strict proof.
🎯 Deriving Infinite Expressions for Pi
This section outlines the process of deriving various infinite expressions for pi from Euler's product formula for sine. The paragraph discusses the challenge of transforming a product into a sum or fraction and introduces logarithms as a tool for this conversion. It then explores specific values to substitute into Euler's formula to yield different identities for pi, such as plugging in pi/2 and pi/4 to obtain Wallis' product and the Leibniz-Madhava formula, respectively. The paragraph also touches on the differentiation of logarithms to simplify expressions and the exploration of infinite sums and continued fractions.
✨ Transforming Sums into Fractions
The focus shifts to converting the Leibniz-Madhava formula into an infinite fraction, showcasing a clever mathematical manipulation involving adjusting the equation and employing a 'combo move' to simplify the expression. The paragraph demonstrates how to transform the sum into a fraction by adding and subtracting terms, and then dividing by a common factor to achieve a simplified form. The result is an infinite fraction that is equivalent to the original sum, leading to Brouncker's infinite fraction formula. The paragraph highlights the beauty and ingenuity of these mathematical transformations.
🌟 Euler's Basel Problem and Beyond
This paragraph discusses Euler's work on the Basel problem, which involved finding a closed-form expression for the sum of the reciprocals of the squares of the natural numbers. Euler's approach involved expanding the infinite product for sine, collecting terms, and differentiating to eliminate powers of x. The paragraph explains how Euler derived the Basel formula by setting x to zero after differentiating the expanded product. It also mentions Euler's further exploration, leading to an infinite series of formulas for higher powers of pi, connected to the Riemann zeta-function and Bernoulli numbers.
📘 Reflections on Euler's Methods and Homework Challenge
The final paragraph reflects on the non-rigorous nature of Euler's 'Nike method' of mathematical discovery, which involved making大胆的猜想 and observing outcomes rather than strict proof. It emphasizes the importance of rigorous proof in mathematics and invites viewers to engage with the material by attempting to derive pi to the power of six as a challenge. The paragraph also hints at the need for a deeper understanding of certain details in the derivations presented and mentions Euler's general super formula related to the Riemann zeta-function, encouraging viewers to explore further.
Mindmap
Keywords
💡Leonhard Euler
💡Infinite Product
💡Pi (π)
💡Maclaurin Series
💡Logarithm
💡Differentiation
💡Euler's Product Formula
💡Wallis's Infinite Product Formula
💡Basel Problem
💡Riemann Zeta-Function
💡Weierstrass Factorisation Theorem
Highlights
Introduction to Euler's mathematical leap of faith and its impact on formulas for pi.
Euler's infinite product formula for sine and its derivation through a creative process.
The concept of treating functions like sine as infinite polynomials and Euler's innovative approach.
Euler's method of ignoring the Maclaurin series to derive a new formula for sine.
The idea of multiplying out factors of sine's zeros to form an infinite product.
Euler's technique of dividing by X to determine the constant in the sine formula.
The use of limits to handle the undefined behavior of sine X divided by X at zero.
The transformation of Euler's sine product into a formula involving pi.
Derivation of the Leibniz-Madhava formula for pi from Euler's product formula.
The conversion of a product into a sum using logarithms and differentiation.
Obtaining the Leibniz-Madhava formula by evaluating at PI over 4.
Ingenious derivation of an infinite fraction from the Leibniz-Madhava sum formula.
The connection between infinite fractions and sums, and their equal partial values.
Euler's Basel formula and its derivation from the sine product formula.
The generalization of Euler's Basel formula to infinitely many formulas for even powers of pi.
The exploration of the Weierstrass factorization theorem and its relation to Euler's work.
Challenges for the audience to derive the PI to the power of six formula and to scrutinize the rigorous proofs.
Final thoughts on Euler's contributions and the importance of both creative insights and rigorous proofs in mathematics.
Transcripts
Browse More Related Video
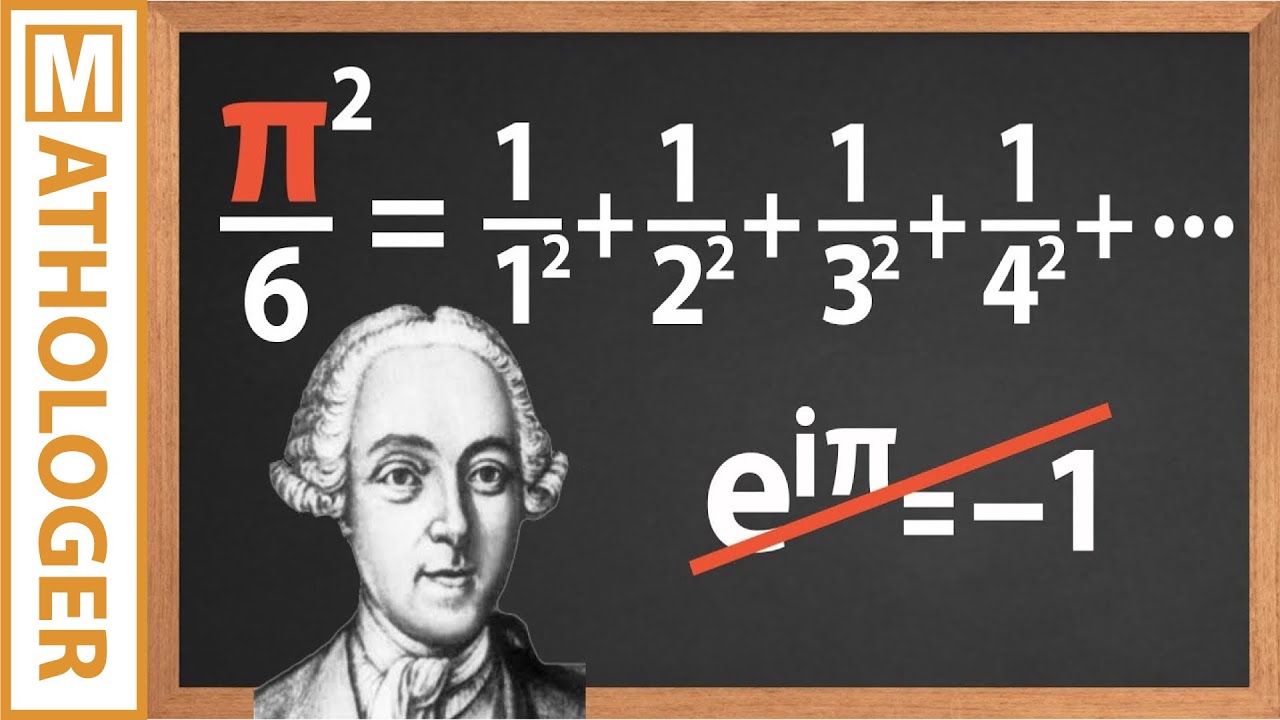
Euler's real identity NOT e to the i pi = -1

Pi is IRRATIONAL: animation of a gorgeous proof

Ramanujan's easiest hard infinity monster (Mathologer Masterclass)

How did Ramanujan solve the STRAND puzzle?

e (Euler's Number) is seriously everywhere | The strange times it shows up and why it's so important
Calculus Chapter 1 Lecture 2 Exponentials
5.0 / 5 (0 votes)
Thanks for rating: