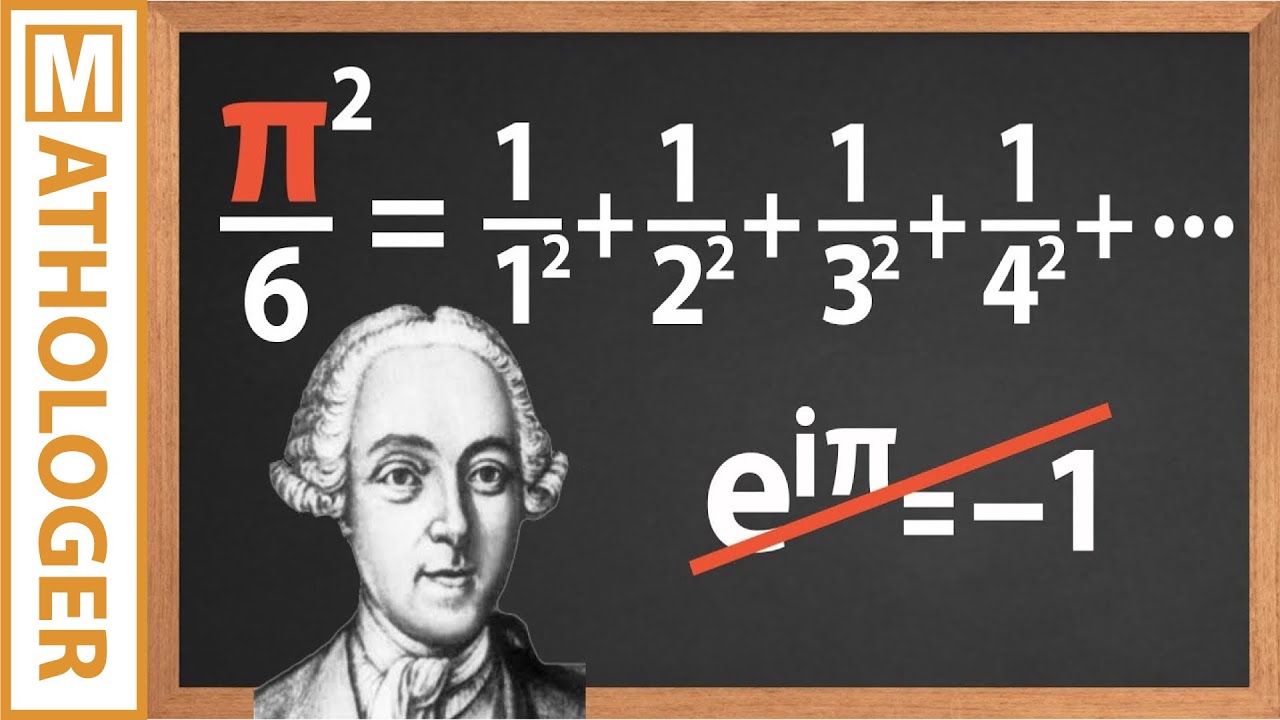Pi is IRRATIONAL: animation of a gorgeous proof

Mathologer

23 Dec 201723:19

EducationalLearning

32 Likes 10 Comments

TLDRIn this Mathologer video, the focus is on proving the irrationality of pi, a concept often accepted without understanding. The script introduces Lambert's 1761 proof, the first of its kind, using animated algebra to make the complex process more accessible. It begins with a simple irrationality proof for log 3, then dives into Lambert's formula for the tangent function, demonstrating its transformation into an infinite fraction. The video also contextualizes Lambert's work with Euler's influence on continued fractions, illustrating the mathematical journey from a valid formula to proving pi's irrationality through an infinite descent argument, concluding with a special Mathologer seal of approval for viewers who grasp the entire concept.

Takeaways

📚 The video discusses the irrationality of numbers such as root 2, pi, and e, which cannot be expressed as ratios of integers.
🔍 It highlights that while proofs for the irrationality of root 2 and e are well-known, a proof for pi's irrationality is less commonly understood.
🎓 Johann Lambert's 1761 proof is the first demonstration of pi's irrationality, which the video aims to make accessible through animated algebra.
🔑 Lambert's proof involves a three-step process: establishing a formula for the tangent function, showing that tangent of any rational number (except zero) is irrational, and concluding that pi is irrational because tan(pi/4) equals 1.
📈 The video provides a simplified proof for the irrationality of log 3 to serve as a warm-up for the main proof.
📐 Lambert's formula for tan(x) is derived from the infinite sums of sine and cosine functions, transforming them into an infinite continued fraction.
🌟 Euler's work with infinite fractions and his proof of the irrationality of e influenced Lambert's approach to proving pi's irrationality.
📉 The transformation of the infinite sum into Lambert's fraction involves complex algebraic manipulations, which are visualized through animations in the video.
📝 The video acknowledges that while the graphical approximations suggest the equality of tan(x) and the infinite fraction, a rigorous proof is still required.
🧩 Lambert's proof concludes with an infinite descent argument, showing that assuming the rationality of the tangent of a rational number leads to an impossible scenario, thus proving its irrationality.
🎄 The video ends with a festive note, wishing viewers a Merry Christmas and promising to continue the exploration of mathematical concepts in the new year.

Q & A

What are the three key irrational numbers mentioned in the video?
-The three key irrational numbers mentioned in the video are root 2, pi, and e.
Why are the proofs for the irrationality of pi considered to be less known than those for root 2 and e?
-The proofs for the irrationality of pi are less known because they are very technical and mostly unintuitive, making them less accessible to a general audience.
Who was the first to prove the irrationality of pi, and in what year was this proof published?
-Johann Lambert was the first to prove the irrationality of pi, and his proof was published in 1761.
What is the main method used by Lambert in his proof of the irrationality of pi?
-Lambert's main method involves proving a new formula for the tangent function and showing that if you plug in any rational number for x (other than 0), you always get an irrational number.
What is the significance of tan(x) being equal to 1 in Lambert's proof?
-The fact that tan(pi/4) equals 1 is significant because it implies that pi/4 cannot be written as a fraction, which in turn implies that pi itself is irrational.
What is the relationship between Lambert's work and Euler's work on infinite nested fractions?
-Lambert was a contemporary of Euler, and both were colleagues at the Prussian Academy of Sciences in Berlin. Euler had popularized the use of continued fractions (infinite nested fractions) to prove various mathematical results, which likely influenced Lambert's approach to turning tan(x) into an infinite fraction.
What is the purpose of Euler's special type of infinite fraction in the context of irrationality proofs?
-Euler's special type of infinite fraction, where all numerators are 1 and all denominators are positive integers, is used to show that any number written in this form is irrational.
How does Lambert transform the infinite sum of sin(x) and cos(x) into an infinite fraction?
-Lambert uses algebraic manipulations, including factoring out common terms, applying the reciprocal trick, and adding and subtracting terms to transform the infinite sum into an infinite fraction.
What is the concept of 'infinite descent' used in the proof of irrationality?
-The concept of 'infinite descent' is a method of proof by contradiction, where the assumption that a number is rational leads to an infinite sequence of ever-decreasing positive integers, which is impossible, thus proving the number must be irrational.
What is the conclusion of the video regarding the irrationality of pi?
-The video concludes that pi is irrational, based on Lambert's proof which involves showing that tan(x) can be represented as an infinite fraction and that this fraction is irrational when x is a nonzero rational number.

Outlines

00:00

📚 Introduction to Irrational Numbers and Lambert's Proof

The video script begins with an introduction to the concept of irrational numbers, specifically mentioning root 2, pi, and e. It acknowledges that while many viewers are aware of the irrationality of these numbers, few can explain why pi is irrational. The script introduces Johann Lambert's 1761 proof of pi's irrationality, which is the focus of the video. The presenter aims to make this complex proof more accessible through animated algebra. The script also provides a simple example of proving the irrationality of log 3, setting the stage for the more intricate proof to follow.

05:04

🔍 Lambert's Infinite Fraction and Historical Context

This paragraph delves into Lambert's groundbreaking formula for the tangent function, expressed as an infinite fraction involving odd numbers. The script explains how Lambert's formula leads to the conclusion that the tangent of any rational number (except zero) results in an irrational number. The historical context is provided, mentioning Lambert's contemporary, Leonhard Euler, and the popularity of continued fractions at the time. Euler's work with infinite fractions and their connection to irrational numbers is highlighted, setting the stage for Lambert's innovative approach to proving pi's irrationality.

10:05

🎨 Transforming Tan(x) into an Infinite Fraction

The script describes the process of transforming the basic trigonometric identity of tan(x) into Lambert's infinite fraction. It involves using the infinite series representations of sine and cosine functions and applying algebraic manipulations, including a 'reciprocal trick' to gradually shape the expression into an infinite fraction. The paragraph emphasizes the complexity of the transformation and the presenter's effort to simplify it through animations, ensuring the audience can follow the intricate algebra involved.

15:10

📉 Graphical Representation and Convergence of Infinite Fractions

This section discusses the graphical representation of the tangent function and its approximations using partial fractions derived from Lambert's infinite fraction. The script explains how these partial fractions converge to the tangent function as more terms are included, visually demonstrating the accuracy of the approximation. However, it also points out the need for a rigorous proof to justify the equality between the tangent function and the infinite fraction, acknowledging that the graphical evidence and initial formula are not sufficient on their own.

20:11

🔧 Proof of Irrationality Using Infinite Descent

The final paragraph presents the culmination of Lambert's proof, which involves assuming the rationality of the tangent of a fraction and deriving an infinite sequence of ever-decreasing positive integers, leading to a contradiction. This 'infinite descent' argument is used to establish the irrationality of the tangent of a fraction, and by extension, the irrationality of pi. The script concludes with a summary of the proof's elegance and the presenter's invitation for feedback from the audience, along with well-wishes for the holiday season.

Mindmap

Keywords

💡Irrational Numbers

Irrational numbers are real numbers that cannot be expressed as a simple fraction — that is, the ratio of two integers. They have non-repeating, non-terminating decimal expansions. In the context of the video, the theme revolves around proving that certain well-known mathematical constants, such as pi (π), are indeed irrational. The video script mentions that most viewers are aware of the irrationality of numbers like root 2 and e, but may not be familiar with the proof for pi.

💡Proof

A proof in mathematics is a logical argument that establishes the truth of a proposition or theorem. The script discusses various proofs of irrationality, specifically focusing on Johann Lambert's proof for the irrationality of pi. The proof is a central theme of the video, with the presenter aiming to make the complex proof more accessible through animated algebra.

💡Johann Lambert

Johann Lambert was an 18th-century Swiss mathematician known for his work in a variety of mathematical fields. The script highlights his significance as the first person to provide a proof of the irrationality of pi, which is the main focus of the video. His approach to proving pi's irrationality is explained through a series of animated steps.

💡Tangent Function

The tangent function (tan) is a trigonometric function that relates the angles of a right triangle to the ratios of its sides. In the script, Lambert's proof involves a novel formula for the tangent function, which is a key component in his proof for the irrationality of pi. The formula is expressed as an infinite series involving odd numbers.

💡Infinite Series

An infinite series is a sequence of numbers that does not have a final term and can be thought of as adding up infinitely many terms. In the video script, the tangent function is expressed as an infinite series, which is a crucial step in Lambert's proof. The series is manipulated algebraically to eventually demonstrate the irrationality of pi.

💡Continued Fractions

Continued fractions are expressions that can be used to represent real numbers in a form that continues indefinitely. The script mentions Euler's work with continued fractions and how they were popular among mathematicians of the time. Lambert's proof involves transforming the tangent function into an infinite fraction, which is a type of continued fraction.

💡Logarithm

A logarithm is the inverse operation to exponentiation, used to solve for an exponent knowing the base and the result. The script begins with a simple proof of the irrationality of the logarithm of 3, using the properties of exponents and the fact that certain numbers cannot be both odd and even, setting the stage for more complex proofs.

💡Pi (π)

Pi, often denoted as π, is a mathematical constant representing the ratio of a circle's circumference to its diameter. The script's main objective is to explain Lambert's proof that pi is an irrational number. The proof's conclusion that pi is irrational is reached by showing that π/4 is irrational, and thus π must also be irrational.

💡Algebraic Manipulation

Algebraic manipulation refers to the process of transforming one equation or expression into another through a series of algebraic steps. The script describes a complex series of algebraic manipulations that Lambert used to derive his formula for the tangent function, which is essential for proving the irrationality of pi.

💡Infinite Descent

Infinite descent is a method of proof that involves showing that a certain property, if assumed to be true, would lead to an infinite sequence of steps, each smaller than the previous, which is logically impossible. The script uses this method to argue that certain infinite fractions, if rational, would lead to an infinite descent of positive integers, thus proving they must be irrational.

Highlights

Introduction to the concept of irrational numbers and the challenge of proving the irrationality of pi.

Johann Lambert's 1761 proof of the irrationality of pi, the first of its kind.

A simplified irrationality proof for log 3 using powers of 10.

Lambert's approach to proving pi's irrationality through an animated algebraic process.

The three-step summary of Lambert's proof involving a new formula for the tangent function.

Lambert's formula for tan x as an infinite series involving odd numbers.

The demonstration that tan(x) is irrational for any rational x, leading to the conclusion about pi.

The use of tan(pi/4) = 1 to deduce the irrationality of pi/4, and by extension, pi.

Historical context of Lambert's work and its relation to Euler's influence on infinite fractions.

Euler's proof of the irrationality of numbers represented by simple infinite fractions.

Lambert's transformation of the tangent function into an infinite fraction and the challenges involved.

The graphical representation of the convergence of partial fractions to tan x.

The need for a rigorous proof of the equality between tan x and the infinite fraction.

Lambert's method of proving the irrationality of tan(x) for rational x by transforming the infinite fraction.

The infinite descent argument used to prove the irrationality of the transformed infinite fraction.

Conclusion of the proof and the appreciation for the beauty of Lambert's argument.

Transcripts

Browse More Related Video

How did Ramanujan solve the STRAND puzzle?

Euler's infinite pi formula generator

Euler's real identity NOT e to the i pi = -1

A proof that e is irrational - Numberphile

BusCalc 09 Why the Power Rule?

Ramanujan's easiest hard infinity monster (Mathologer Masterclass)

Related Tags

Math Proof Irrational Numbers Pi History Lambert Proof Infinite Series Algebra Animation Euler Fractions Rationality Test Mathologer Video Educational Content